A. Warm sign in
E. Equidistant
Given an n-node tree and several points, ask if we can find a point in the tree, and the distance from these points is the same
Solution idea: we put these points in at the same time and perform BFS operation, and we open an array to record the number of shortest paths from several final nodes to here. Therefore, for each passing node, if we have dis[x] == dis[h] + 1, then cnt[x] += cnt[h]. If dis [x] > dis [H] + 1, then cnt[x] = cnt[h]
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 10;
const int inf = 0x3f3f3f3f;
vector<int> G[maxn];
queue<int> q;
int cnt[maxn];
int dis[maxn];
int n,m;
void BFS()
{
while(!q.empty())
{
int x = q.front();
q.pop();
for(int f : G[x])
{
if(dis[f] == dis[x] + 1) cnt[f] += cnt[x];
else if(dis[f] > dis[x] + 1)
{
dis[f] = dis[x] + 1;
cnt[f] = cnt[x];
q.push(f);
}
}
}
}
void solve()
{
scanf("%d %d",&n,&m);
memset(dis,inf,sizeof dis);
for(int i = 1;i <= n - 1;++i)
{
int u,v;
scanf("%d %d",&u,&v);
G[u].emplace_back(v);
G[v].emplace_back(u);
}
int pos;
for(int i = 1;i <= m;++i)
{
scanf("%d",&pos);
dis[pos] = 0;
cnt[pos] = 1;
q.push(pos);
}
//cout << "??"<<"\n";
BFS();
for(int i = 1;i <= n;++i)
{
//cout<<i<<" "<< cnt[i] <<"\n";
if(cnt[i] == m)
{
printf("YES\n%d\n",i);
return;
}
}
printf("NO\n");
}
int main()
{
solve();
return 0;
}
I-Ideal Pyramid
Given n points in three-dimensional space, find a minimum pyramid, which can contain all these points in the cone and output the coordinates of the corresponding vertices
Problem analysis: since this problem seeks the minimum height, we can know that there must be a column tangent to the face of the pyramid. For any point (non vertex) (xi,yi,zi) on the pyramid and its vertex (x,y,z), we can list such a formula for X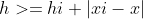
, then we can also split this absolute value. If the formula is greater than or equal to 0, we can obtain the left and right boundaries of x. at the same time, we can also obtain the left and right boundaries of Y. then the last point is (XL + XR > > 1, YL + yr > > 1). For the height, we need to take the relatively long one of x and y, So we can also output the final result
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
typedef long long ll;
const ll inf = 0x3f3f3f3f3f3f3f3f;
ll xr = - inf,xl = inf,yr = - inf,yl = inf;
ll x,y,h;
int n;
int main()
{
scanf("%d",&n);
for(int i = 1;i <= n;++i)
{
scanf("%lld %lld %lld",&x,&y,&h);
xr = max(h + x,xr);
xl = min(x - h,xl);
yr = max(h + y,yr);
yl = min(y - h,yl);
}
printf("%lld %lld %lld\n",(xr + xl) >> 1,(yl + yr) >> 1,max((xr - xl + 1),(yr - yl + 1)) >> 1);
return 0;
}M-Managing Difficulties
Find a sequence that satisfies aj - ai = ak - aj
Solution: first analyze the data range of 2000, then the time complexity of n^2 is certainly acceptable. Then we can first calculate the previous 2 aj - ai, and finally read in the answer when ak is entered (note that using unordered_map, and when using count, the time complexity will be less than that of direct query)
#include <bits/stdc++.h>
using namespace std;
int T,n;
long long ans;
const int maxn = 2e3 + 10;
int a[maxn];
unordered_map<int,int> mp;
int tmp;
void solve()
{
scanf("%d",&n);
ans = 0;
mp.clear();
for(int i = 1;i <= n;++i)
{
scanf("%d",&a[i]);
if(mp.count(a[i]) != 0) ans += mp[a[i]];
for(int j = 1;j < i;++j)
{
mp[2 * a[i] - a[j]]++;
}
}
printf("%lld\n",ans);
}
int main()
{
scanf("%d",&T);
while(T--)
{
solve();
}
return 0;
}J-Just the Last Digit
Given a graph, aij stands for aij% 10 paths from i to j
Problem solving idea: analyze the data range. If the data range is relatively small, we can directly determine whether the corresponding path meets our requirements by enumerating the middle one
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e2 + 10;
int mp[maxn][maxn];
char str[maxn][maxn];
int ans[maxn][maxn];
int n;
void solve()
{
scanf("%d",&n);
//getchar();
for(int i = 1;i <= n;++i)
{
scanf("%s",str[i] + 1);
// printf("%s\n",str[i] + 1);
}
for(int i = 1;i <= n;++i)
{
for(int j = 1;j <= n;++j)
{
//printf("str: %s",str[i]);
mp[i][j] = str[i][j] - '0';
}
}
// for(int i = 1;i <= n;++i)
// {
// for(int j = 1;j <= n;++j)
// {
// printf("%d ",mp[i][j]);
// }
// printf("\n");
// }
for(int k = 1;k <= n;++k)
{
for(int i = 1;i <= n - k;i++)
{
int f = i + k,cnt = 0;
for(int j = i + 1;j < f;++j)
{
cnt = (cnt + ans[i][j] * mp[j][f]) % 10;
}
if(cnt != mp[i][f]) ans[i][f] = 1;
}
}
for(int i = 1;i <= n;++i)
{
for(int j = 1;j <= n;++j)
{
printf("%d",ans[i][j]);
}
printf("\n");
}
}
int main()
{
solve();
return 0;
}