Hello, everyone. I'm an egg.

Today, let's design the linked list and forcibly learn the five operations of the linked list.

Set the bench and open it directly.

LeetCode 707: Design linked list

meaning of the title

Realize the search, header insertion, tail insertion, general insertion and deletion of linked list:

• get(index): get the value of the index node in the linked list. Returns - 1 if the index is invalid.

• addAtHead(val): add a node with value val before the first element of the linked list. After insertion, the new node will become the first node in the linked list.

• addAtTail(val): append the node with value val to the last element of the linked list.

• addAtIndex(index,val): add a node with value val before the index node in the linked list. If the index is equal to the length of the linked list, the node will be attached to the end of the linked list. If the index is greater than the length of the linked list, the node will not be inserted. If the index is less than 0, the node is inserted in the header.

• Delete atindex (index): if the index is valid, delete the index node in the linked list.

Example

Tips

• 1 <= val <= 1000

• 1 < = number of operations < = 1000

• The built-in LinkedList library cannot be used

Topic analysis

Water problem, medium difficulty, investigate the routine operation of the linked list.

If you are not familiar with the linked list, please see the following article:

Linked list, just draw a few times!

Carefully, this question mainly involves five operations:

• Find the value of the index node in the linked list

• Insert a node before the first node in the linked list

• Insert a node after the last node in the linked list

• Insert a node before the index node of the linked list

• Delete the index node of the linked list.

These five kinds of common addition, deletion and query operations including the linked list are excellent exercises for smelly treasures who have just learned the linked list to consolidate their knowledge in time.

I use the single linked list of the leading node to realize this problem.

The head node, which may be called sentinel node by many people, is placed before the node of the first element, and the data field is generally meaningless.

graphic

For the linked list problem, in order to facilitate subsequent operations, a simple node class is generally defined first:

# Custom single node
class Node:
    def __init__(self, data):
        self.val = data
        self.next = None

Initialize the header node and the length of the linked list in the linked list class.

def __init__(self):
        """
        Initialize your data structure here.
        """
        # Head node
        self.head = Node(0)
        # Save linked list length
        self.length = 0

get(index) to find the node. There's nothing to say, just start from the first node. Time complexity O(n).

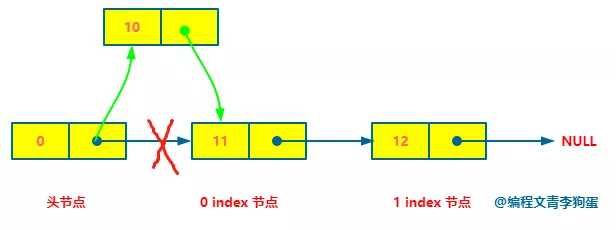
addAtHead(val), insert a node before the first node in the linked list. It's easy to insert. Just find the precursor node of the first node, which is the head node.

Because it is in the first, the time complexity is O(1).

When inserting a linked list, remember that the sequence of insertion operations cannot be changed! Remember!

The subsequent pointer of the node to be inserted must first point to the node to be inserted, and then the precursor node points to the node to be inserted.

In the following figure, the node with a value of 10 points to the node with a value of 11, then the head node with a value of 0 points to the node with a value of 10.

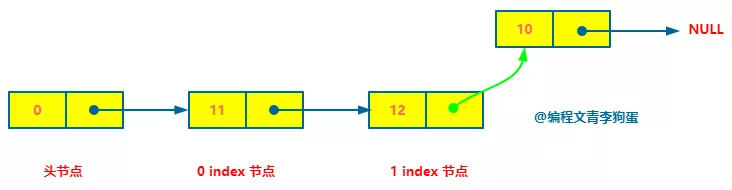
Similarly, addAtTail(val) inserts a node after the last node in the linked list. The precursor node of the node to be inserted is the last node.

Because in the last one, the time complexity O(n).

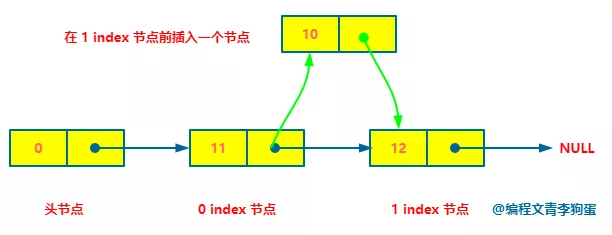
addAtIndex(index, val) inserts a node before the index node in the linked list. In fact, this is the general operation of insertion.

Similarly, the time complexity is O(n) from the first node.

addAtHead(val) is equivalent to addAtIndex(0, val).

addAtTail(val) is equivalent to addAtIndex(length, val).

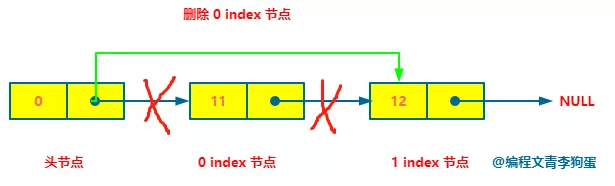
deleteAtIndex(index) deletes the index node of the linked list. It also finds the precursor node of the node to be deleted and deletes it by changing the subsequent pointer of the node.

Similarly, the time complexity of deleting the linked list is O(n).

code implementation

# Custom single node
class Node:
    def __init__(self, data):
        self.val = data
        self.next = None

class MyLinkedList:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        # Head node
        self.head = Node(0)
        # Save linked list length
        self.length = 0

    def get(self, index: int) -> int:
        """
        Get the value of the index-th node in the linked list. If the index is invalid, return -1.
        """
        # Determine whether the entered index is valid
        if index < 0 or index >= self.length:
            return -1

        p = self.head
        i_index = 0

        # range is the left closed right open interval, equivalent to [0,index+1)
        for _ in range(index + 1):
            p = p.next

        return p.val

    def addAtHead(self, val: int) -> None:
        """
        Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list.
        """
        return self.addAtIndex(0, val)

    def addAtTail(self, val: int) -> None:
        """
        Append a node of value val to the last element of the linked list.
        """
        return self.addAtIndex(self.length, val)

    def addAtIndex(self, index: int, val: int) -> None:
        """
        Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted.
        """
        # In the special case of index < 0 and index = 0, it means head interpolation
        if index < 0:
            index = 0
        if index > self.length:
            return

        p = self.head
        add_node = Node(val)

        # Find the precursor node of the index node
        for _ in range(index):
            p = p.next

        add_node.next = p.next
        p.next = add_node

        # Insert node, linked list length + 1
        self.length += 1

    def deleteAtIndex(self, index: int) -> None:
        """
        Delete the index-th node in the linked list, if the index is valid.
        """
        # Determine whether the entered index is valid
        if index < 0 or index >=self.length:
            return

        p = self.head
        # Find the precursor node of the node to be deleted and the node to be deleted
        for _ in range(index + 1):
            # Precursor node
            pre = p
            # To delete a node
            p = p.next

        pre.next = p.next

        # Free memory for deleting nodes
        p = None

        # Delete node, linked list length - 1
        self.length -= 1

# Your MyLinkedList object will be instantiated and called as such:
# obj = MyLinkedList()
# param_1 = obj.get(index)
# obj.addAtHead(val)
# obj.addAtTail(val)
# obj.addAtIndex(index,val)
# obj.deleteAtIndex(index)

Well, the graphic design list is over.

Smelly treasure, who has a weak foundation, thinks about this problem. When he wants to understand it, he will take the first step to learn the linked list well.

After reading is true love, click the praise message to take off for Ben Dan~

I'm an egg. I'll see you next time!