image convolution

1 cross correlation operation

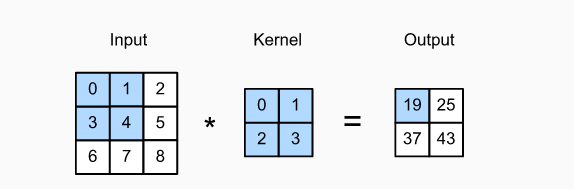
Strictly speaking, convolution layer is a wrong name, because the operation it expresses is actually cross-correlation operation, not convolution operation. In the convolution layer, the input tensor and kernel tensor generate the output tensor through cross-correlation operation. First, let's ignore the channel (the third dimension) temporarily and see how to deal with the two-dimensional image data and hidden representation. In the following figure, the input is a two-dimensional tensor with a height of 3 and a width of 3 (that is, the shape is 3) × 3 ). The height and width of the convolution kernel are 2, and the shape of the convolution kernel window (or convolution window) is determined by the height and width of the kernel (i.e. 2) × 2 ).

import torch
from torch import nn
from d2l import torch as d2l


def corr2d(X, K):  #@save
    """Calculate two-dimensional cross-correlation operation."""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

2 convolution
The convolution layer performs cross-correlation operation on the input and convolution kernel weight, and generates the output after adding scalar bias. Therefore, the two trained parameters in the convolution layer are convolution kernel weight and scalar bias. Just like the random initialization of the full connection layer before, when training the convolution layer based model, we also randomly initialize the convolution kernel weight. The two-dimensional convolution layer is realized based on the corr2d function defined above. In the init constructor, declare weight and bias as two model parameters. The forward propagation function calls the corr2d function and adds an offset.

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

3 edge detection of target in image
The following is a simple application of convolution layer: by finding the position of pixel change, we can detect the edges of different colors in the image. First, we construct a 6 × 8 pixel black and white image. The middle four columns are black (0), and the other pixels are white (1).

X = torch.ones((6, 8))
X[:, 2:6] = 0
X

Next, we construct a convolution kernel K with a height of 1 and a width of 2. When performing cross-correlation operation, if the two horizontally adjacent elements are the same, the output is zero, otherwise the output is non-zero.

K = torch.tensor([[1.0, -1.0]])

Now, we perform a cross-correlation operation on parameters X (input) and K (convolution kernel). As shown below, 1 in the output Y represents the edge from white to black, - 1 represents the edge from black to white, and the output in other cases is 0.

Y = corr2d(X, K)
Y

tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])

Now we transpose the input two-dimensional image, and then perform the above cross-correlation operation. The output is as follows, and the previously detected vertical edge disappears. As expected, this convolution kernel K can only detect vertical edges, not horizontal edges.

corr2d(X.t(), K)

tensor([[0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.]])

4 learning convolution kernel

If we only need to find black and white edges, the edge detector of [1, - 1] above is sufficient. However, when there are convolution kernels with more complex values or continuous convolution layers, it is impossible to design filters manually. So can we learn the convolution kernel of Y generated by X? Now let's see if we can learn the convolution kernel of Y generated by X by looking only at the input-output pairs. We first construct a convolution layer and initialize its convolution kernel as a random tensor. Next, in each iteration, we compare the square error between Y and the convolution layer output, and then calculate the gradient to update the convolution kernel. For simplicity, we use the built-in 2D convolution here and ignore the offset.

# A two-dimensional convolution layer is constructed, which has an output channel and a convolution kernel with the shape of (1,2)
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)

# This two-dimensional volume layer uses four-dimensional input and output formats (batch size, channel, height, width),
# The batch size and the number of channels are 1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))

for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # Iterative convolution kernel
    conv2d.weight.data[:] -= 3e-2 * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'batch {i+1}, loss {l.sum():.3f}')
batch 2, loss 9.103
batch 4, loss 1.762
batch 6, loss 0.392
batch 8, loss 0.105
batch 10, loss 0.034

After 10 iterations, the error has been reduced to low enough. Now let's look at the weight tensor of the convolution kernel.

conv2d.weight.data.reshape((1, 2))

tensor([[ 0.9681, -1.0023]])

summary

The core calculation of two-dimensional convolution is two-dimensional cross-correlation operation. The simplest form is to perform cross-correlation between the two-dimensional input data and the convolution kernel, and then add an offset.

We can design a convolution kernel to detect the edge of the image.

We can learn the parameters of convolution kernel from the data.

When learning convolution kernel, whether strict convolution operation or cross-correlation operation is used, the output of convolution layer will not be greatly affected.

When we need to detect a wider region in the input feature, we can build a deeper convolution network.