After reading Alex net's paper.

This paper creatively uses many structures and tips in convolutional neural networks. It is highly recommended that you read this paper at the foundation level of neural networks.

outline

A method of color enhancement based on PCA is introduced in AlexNet. The effect is that the lightness (brightness) of the picture will change as a whole, and there is no change in the picture structure or obvious change in color difference.

The effect is as follows:

• The brightness of the image has changed significantly, some dark and some bright, and the outline of the main things in the picture is still very clear without change;
• The dominant color of things has not changed (the dominant green color of the leaves above has not changed);
• The relative color difference of the picture has not changed (the contrast between the dark and bright parts of the original picture still exists)

Implementation method in this paper

Here I will briefly describe the implementation method in this paper:
Implementation steps:

1. Normalize the picture according to RGB three channels, with the mean value of 0 and the variance of 1.
   It is worth mentioning that the processing is carried out according to RGB three channels, because we carry out color enhancement. In the pictures of RGB three channels, the relative relationship between RGB determines the image color, and we cannot change the pixel value distribution inside the three channels.
2. Flatten the picture according to channel to a size of (?)?, 3) array of
3. Find the covariance matrix of the above array
4. Eigendecomposition of covariance matrix
5. Of the following formula p \mathbf{p} p is the eigenvector, λ \lambda λ Is the eigenvalue, α \alpha α That is, the jitter coefficient added for us
   [ p 1 p 2 p 3 ] [ α 1 λ 1 α 2 λ 2 α 3 λ 3 ] T \begin{bmatrix}\mathbf{p}_1 & \mathbf{p}_2 & \mathbf{p}_3\end{bmatrix} \begin{bmatrix}\alpha_1\lambda_1 & \alpha_2\lambda_2 & \alpha_3\lambda_3 \end{bmatrix}^T [p1​​p2​​p3​​][α1​λ1​​α2​λ2​​α3​λ3​​]T
   The matrix composed of eigenvectors is 3x3, and the array composed of eigenvalues multiplied by dithering coefficient is 3x1, so the array obtained by point multiplication is exactly 3x1. The three values are added to the R, G and B channels of the original image respectively, which is the final enhanced image.

I understand

Because there is no clear explanation in the paper why I want to do this, I'll give a general explanation of my understanding

• Why use PCA principal component analysis??
  Because we want to maintain the relative color difference, main color system and contour of the original image, we can't change the things expressed by the image itself after enhancing the data.
  We PCA the three channels. The eigenvector of the covariance matrix expresses the relative relationship between the three channels R, G and B. for example, in the picture of the leaves above, green is dominant, the color difference is mainly reflected by green, the color system of green is relatively rich, and the principal component is partial to green.
  The following is the amplitude of jitter in 8 enhancements (R,G,B three channels)
  

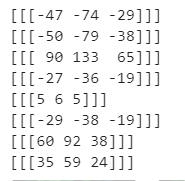
We can clearly see that the absolute value of the second value in each line is the largest, that is, the jitter amplitude on the green channel is the largest. This is the role of PCA principal component to find out the main color system in the picture and greatly change the value of the main color system, so that the overall tone of the whole image does not change.

As an extreme example, if the pixel of the image has only the value of channel G and the values of channel R and channel B are 0, the whole image is a green image with different light and shade. The disturbance value obtained by PCA principal component analysis only has the value of channel G, and the values of channel R and channel B will still be 0, because there is no information of R and B images in the original image, PCA will not get the main component values of these two channels, so it will not add values that are not in the original image to the image.

PCA principal component analysis will divide the weight according to the information of the data in the three channels in the original image (i.e. the eigenvalue of the covariance matrix)

Code

from numpy import linalg
import numpy as np
from PIL import Image
import random
import matplotlib.pyplot as plt
plt.style.use('seaborn')

def pca_color_augmention(image_array):
    '''
    image augmention: PCA jitter 
    :param image_array: image array
    :return img2: after PCA-jitter Enhanced image array
    '''
    assert image_array.dtype == 'uint8'
    assert image_array.ndim == 3
    # The input image should be (w, h, 3) such a three channel distribution
    
    img1 = image_array.astype('float32') / 255.0
    # Calculate the variance and mean of R, G and B channels respectively
    mean = img1.mean(axis = 0).mean(axis = 0)
    std = img1.reshape((-1, 3)).std()    # img1.std(axis = 0).std(axis = 0) cannot be used
    
    # Standardize the image according to channel (mean value is 0 and variance is 1)
    img1 = (img1 - mean) / (std)
    
    # Expand the image into three strips according to three channels
    img1 = img1.reshape((-1, 3))
    
    # PCA operation on matrix
    # Find the covariance matrix of the matrix
    cov = np.cov(img1, rowvar = False)
    # Finding eigenvalues and vectors of covariance matrix
    eigValue, eigVector = linalg.eig(cov)

    # Jitter coefficient (standard distribution with mean value of 0 and variance of 0.1)
    rand = np.array([random.normalvariate(0, 0.2) for i in range(3)])
    jitter = np.dot(eigVector, eigValue * rand)
    
    jitter = (jitter * 255).astype(np.int32)[np.newaxis, np.newaxis, :]

    img2 = np.clip(image_array + jitter, 0, 255)
    
    return img2

def show_image(image_array):
    for _ in range(8):
    
        ax = plt.subplot(241 + _)
        ax.imshow(pca_color_augmention(image_array))
        ax.axis('off')
    plt.show()

img_tensor = np.array(Image.open('./images/leaf.jpg'))
show_image(img_tensor)

reference resources

The code part of the following article is very detailed, and my code has made some changes on his basis
Let's use PCA color enhancement

attach

Attach leaf.jpg