Q1 channel switching
1.1 leading knowledge
1. imread() reads of CV2 are arranged in BGR order;
2. The gray image of single channel is represented by two-dimensional gray matrix: height * width;
3. The representation method of three channel color image is three-dimensional BGR/RGB matrix: height * width * channel;
4. In order to facilitate processing, the three channel color image matrix can be represented by channels, that is, it can be divided into three two-dimensional matrices.
1.2 implementation code
import cv2
def BGR2RGB(img):
b = img[:,:,0].copy() #First channel b
g = img[:,:,1].copy() #Second channel g
r = img[:,:,2].copy() #Third channel r
img[:,:,0] = r
img[:,:,1] = g
img[:,:,2] = b
return img
img = cv2.imread('imori.jpg')
print(img)
print('\n')
img_trans = BGR2RGB(img)
print(img_trans)
cv2.imwrite('answer_1.jpg',img_trans)
cv2.imshow('result',img_trans)
cv2.waitKey(0)
cv2.destroyAllWindow()
1.3 result analysis


Original image (left), image after channel transformation (right)
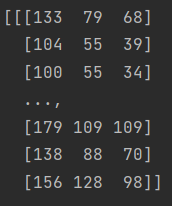
(the "first" data of the image matrix read out without conversion)

(the "first" data after channel conversion)
It can be seen that the data of the third dimension has been exchanged with the data of the first dimension, that is, the original BGR has become RGB.
Q2 grayscale
2.1 leading knowledge
1. Calculation formula: Y = 0.2126*R + 0.7152*G + 0.0722*B;
2. In order to facilitate processing, the image is represented by channels (often used);
3. Note that the final calculated result is a numerical matrix, which we need to convert into a data format that can be processed as an image unit8.
2.2 code implementation
def BGR2GREY(img):
b = img[:, :, 0].copy()
g = img[:, :, 1].copy()
r = img[:, :, 2].copy()
#Gray conversion
out = 0.2126*r + 0.7152*g + 0.0722*b
#out is converted into a data format that can be processed as an image matrix
out = out.astype(np.uint8)
return out2.3 result analysis
 Grayed image
Grayed image
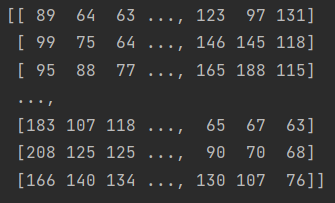 Gray matrix
Gray matrix
Compared with the three channel BGR matrix, the gray matrix is a two-dimensional matrix, and each element represents the gray value of the pixel.
Q3 binarization
3.1 leading knowledge
1. Binarization means that a gray value threshold is set for the grayed image. When the gray value of a pixel is greater than this threshold, the gray value of the point is changed to 255, and when it is less than the threshold, it is changed to 0. In other words, the gray value is polarized, and the final result is a black-and-white image;
2. The gray value is 0 - white, and the gray value is 255 - black.
3.2 code implementation
def binarization(img, th = 128):
lens = len(img)
for i in range(lens-1):
for j in range(lens-1):
if img[i,j] < th:
img[i,j] = 0
else:
img[i,j] = 255
return img
'''Another simple method:
def binarization(img, th = 128):
img[img < th] = 0
img[img >= th] = 255'''3.3 result analysis
 Binary image
Binary image
Q4 Otsu threshold segmentation algorithm (maximum interclass variance method)
4.1 leading knowledge
Otsu algorithm principle: select a threshold through statistical method to separate the foreground color and background color as much as possible.
Judgment basis for optimal segmentation: intra class variance or the variance within the class
Set the average gray value of the whole image as M. Now select a gray value t arbitrarily, and the histogram can be divided into two parts. We call these two parts A and B respectively. The corresponding foreground and background colors. The average values of these two parts are MA and MB. The proportion of the number of pixels in part a to the total number of pixels is recorded as PA, and the proportion of the number of pixels in part B to the total number of pixels is recorded as PB.
The definition of inter class variance given by Nobuyuki Otsu is:
ICV=PA∗(MA−M)^2+PB∗(MB−M)^2
Equivalent formula (see resources for derivation):
ICV=PA*PB*(MA-MB)^2
Traversing every possible gray value threshold and finding the gray threshold that maximizes the variance between classes is the optimal segmentation threshold.
4.2 code implementation
#otsu threshold segmentation algorithm (maximum interclass variance method)
def otsu_thresh(img):
max_vari = -1 #Initialize maximum interclass variance
max_th = 0 #Initialize optimal threshold
for th in range(1,254):
m0 = img[img <= th].mean()
m1 = img[img > th].mean()
w0 = img[img <= th].size
w1 = img[img > th].size
vari = w0*w1/((w0+w1)**2)*((m0-m1)**2)
if vari > max_vari:
max_th = th
max_vari = vari
img_otsu = binarization(img, max_th)
return img_otsu, max_th4.3 result analysis
reference material
Q1 CV2 module usage (detailed tutorial) _zhangfeiwang CSDN blog _cv2
Q2 Opencv: storing images with uint8 type in numpy_ Quiet Zhiyuan * blog - CSDN blog_ np.unit8
Q4 Automatic threshold segmentation of gray image (otsu method) _Ivan's column CSDN blog _otsuthreshold segmentation algorithm;
OTSU threshold segmentation algorithm (OTSU image processing) my blog CSDN blog OTSU threshold segmentation