preface

Image size, flipping and affine transformation in opencv

1, Image size transformation

Function prototype:

void resize(InputArray src, OutputArray dst, Size dsize, double fx=0, double fy=0, int interpolation = INTER_LINEAR)

src: input image

dst: output image. The data type of image is the same as src

dsize: output image size

fx: scale factor of horizontal axis

Scale factor of vertical axis: fy

Interpolation: Flag of interpolation method

Generally, dsize and fx (fy) can use one of them. In case of inconsistency between the final adjustment results of dsize and fx, dsize shall prevail

The interpolation selected for the last parameter will have different effect on the final scaling.

Interpolation method flag table:

Flag parameters	Abbreviation	effect
INTER_NEAREST	0	Nearest neighbor interpolation
INTER_LINEAR	1	bilinear interpolation
INTER_CUBIC	2	Bicubic interpolation
INTER_AREA	3	Resampling using pixel area relationship is preferred for image reduction. The effect of image enlargement is the same as that of INTER_NEAREST similar
INTER_LANCZOS4	4	Lanczos interpolation
INTER_LINEAR_EXACT	5	Bit exact bilinear interpolation
INTER_MAX	7	Interpolation with mask

Example code:

#include<opencv2\opencv. HPP > / / load the header file of OpenCV4
#include<iostream>
#include<vector>
using namespace std;
using namespace cv; //OpenCV namespace

int main()
{
	Mat gray = imread("lena.png", IMREAD_GRAYSCALE);
	if (gray.empty())
	{
		cout << "Please confirm whether the image file name is correct" << endl;
		return -1;
	}
	Mat smallImg, bigImg0, bigImg1, bigImg2;
	resize(gray, smallImg, Size(15, 15), 0, 0, INTER_AREA);  //Reduce the image first
	resize(smallImg, bigImg0, Size(30, 30), 0, 0, INTER_NEAREST);  //Nearest neighbor interpolation
	resize(smallImg, bigImg1, Size(30, 30), 0, 0, INTER_LINEAR);  //bilinear interpolation 
	resize(smallImg, bigImg2, Size(30, 30), 0, 0, INTER_CUBIC);  //Bicubic interpolation
	namedWindow("smallImg", WINDOW_NORMAL);  //If the image size is too small, be sure to set a flag that can adjust the window size
	imshow("smallImg", smallImg);
	namedWindow("bigImg0", WINDOW_NORMAL);
	imshow("bigImg0", bigImg0);
	namedWindow("bigImg1", WINDOW_NORMAL);
	imshow("bigImg1", bigImg1);
	namedWindow("bigImg2", WINDOW_NORMAL);
	imshow("bigImg2", bigImg2);
	waitKey(0);
	return 0;  //Program end
}

smallImg:

bigImg0:

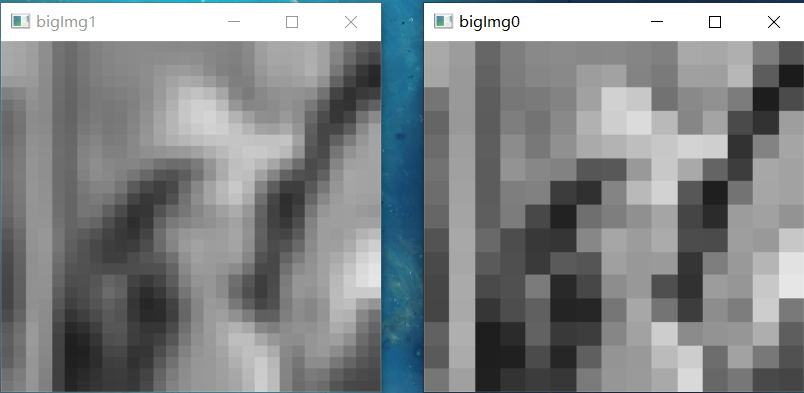
2, Image flip transform

Image flipping model

void flip(InputArray src, OutputArray dst, int flipCode)

src: input image

dst: output image

flipcode: flip mode flag. If the value is greater than 0, it means turning around the y-axis; If the value is equal to 0, it means turning around the x-axis; A value less than 0 indicates flipping around two axes

Sample program:

#include<opencv2\opencv. HPP > / / load the header file of OpenCV4
#include<iostream>
#include<vector>
using namespace std;
using namespace cv; //OpenCV namespace

int main()
{
	Mat img = imread("lena.png");
	if (img.empty())
	{
		cout << "Please confirm whether the image file name is correct" << endl;
		return -1;
	}
	Mat img_x, img_y, img_xy;
	flip(img, img_x, 0);  //Symmetrical with x axis
	flip(img, img_y, 1);  //Symmetric with y axis
	flip(img, img_xy, -1); //Flip first on the x-axis and then on the y-axis
	imshow("img", img);
	imshow("img_x", img_x);
	imshow("img_y", img_y);
	imshow("img_xy", img_xy);
	waitKey(0);
	return 0;  //Program end
}

Triple flip result: img_x, img_y, img_xy

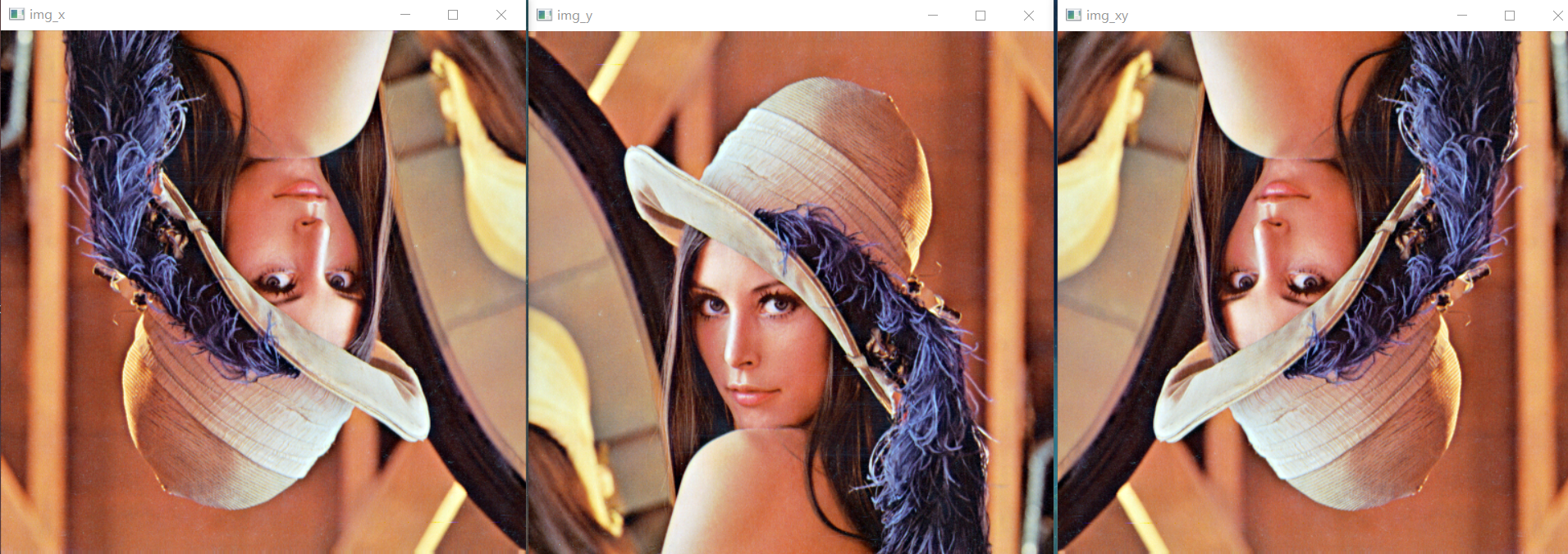
3, Image affine transformation

The affine transformation of the image is used for image rotation. To realize image rotation, we first need to determine the rotation angle and rotation center, then confirm the rotation matrix, and finally realize image rotation through affine transformation.

The getRotationMatrix2D() function is used to calculate the rotation matrix

Mat getRotationMatrix2D(Point2f center, double angle, double scale)

Center: the center position of image rotation

Angle: the rotation angle of the image, in degrees, and a positive value is counterclockwise rotation

Scale: the scale factor of two axes, which can realize the image scaling in the process of rotation. If it is not scaled, enter 1

The image returns a Mat matrix

The function of the other three points corresponding to the transformation matrix M is:

getAffineTransform() function

Mat getAffineTransform(const Point2f src[], const Point2f dst[])

src []: coordinates of 3 pixels in the source image

dst []: coordinates of 3 pixels in the target image

Function returns a 2 * 3 transformation matrix

warpAffine() function prototype

void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags = INTER_LINEAR, int borderMode = BORDER_CONSTANT, const Scalar& borderValue = Scalar())

src: input image

dst: the output image after affine transformation, the same as src data type and the same size as dsize

M: 2 * 3 transformation matrix

dsize: the size of the output image

flags: interpolation method flag

borderMode: mark of pixel boundary extrapolation method

borderValue: the value used to fill the boundary, which is 0 by default

Flag parameters	Abbreviation	effect
INTER_NEAREST	0	Nearest neighbor interpolation
INTER_LINEAR	1	bilinear interpolation
INTER_CUBIC	2	Bicubic interpolation
INTER_AREA	3	Resampling using pixel area relationship is preferred for image reduction. The effect of image enlargement is the same as that of INTER_NEAREST similar
INTER_LANCZOS4	4	Lanczos interpolation
INTER_LINEAR_EXACT	5	Bit exact bilinear interpolation
INTER_MAX	7	Interpolation with mask
WARP_FILL_OUTLIERS	8	Fill all the pixels of the output image. If some pixels fall outside the boundary of the input image, their value is set to fillval
WARP_INVERSE_MAP	16	Set to M inverse transform from output image to input image

Affine transformation is the general term of image rotation, translation and scaling operations, which can be expressed as the superposition of linear transformation and translation transformation. The mathematical representation of affine transformation is to multiply by a linear transformation matrix and add a translation vector.

Sample program:

#include<opencv2\opencv. HPP > / / load the header file of OpenCV4
#include<iostream>
#include<vector>
using namespace std;
using namespace cv; //OpenCV namespace

int main()
{
	Mat img = imread("lena.png");
	if (img.empty())
	{
		cout << "Please confirm whether the image file name is correct" << endl;
		return -1;
	}
	Mat rotation0, rotation1, img_warp0, img_warp1;
	double angle = 45;  //Sets the angle at which the image is rotated
	Size dst_size(img.rows, img.cols);  //Sets the size of the output image
	Point2f center(img.rows / 2.0, img.cols / 2.0);  //Sets the rotation center of the image
	rotation0 = getRotationMatrix2D(center, angle, 1);  //Computing affine transformation matrix
	warpAffine(img, img_warp0, rotation0, dst_size);  //Affine transformation
	imshow("img_warp0", img_warp0);
	//Affine transformation is carried out according to the three defined points
	Point2f src_points[3];
	Point2f dst_points[3];
	src_points[0] = Point2f(0, 0);  //3 points in the original image
	src_points[1] = Point2f(0, (float)(img.cols - 1));
	src_points[2] = Point2f((float)(img.rows - 1), (float)(img.cols - 1));
	//Three points in the image after affine transformation
	dst_points[0] = Point2f((float)(img.rows)*0.11, (float)(img.cols)*0.20);
	dst_points[1] = Point2f((float)(img.rows)*0.15, (float)(img.cols)*0.70);
	dst_points[2] = Point2f((float)(img.rows)*0.81, (float)(img.cols)*0.85);
	rotation1 = getAffineTransform(src_points, dst_points);  //The affine transformation matrix is obtained according to the corresponding points
	warpAffine(img, img_warp1, rotation1, dst_size);  //Affine transformation
	imshow("img_warp1", img_warp1);
	waitKey(0);
	return 0;  //Program end
}

img_warp0:

img_warp1:

Thanks for reading!

You are also welcome to pay attention to Xiaobai blogger and give more encouragement!