Implementation of CF algorithm based on matrix decomposition

Posted by gtibok on Sat, 29 Jan 2022 00:43:03 +0100

Dataset used: link: https://pan.baidu.com/s/1OLQE7mpefXGRpADyVEkpVQ
Extraction code: 7x5c

1, History of matrix decomposition

1.1 Traditional SVD

In general, SVD matrix decomposition refers to SVD (singular value) decomposition technology. Here, we name it Traditional SVD (traditional and classic), and its formula is as follows:

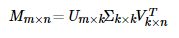
The form of Traditional SVD decomposition is the multiplication of three matrices, and the intermediate matrix is singular value matrix. If you want to use SVD decomposition, one premise is that the matrix is dense, that is, the elements in the matrix must be non empty, otherwise you can't use SVD decomposition.

Obviously, our data is sparse in most cases. Therefore, if we want to use Traditional SVD, the general practice is to fill the matrix with the mean value or other statistical methods first, and then use Traditional SVD to decompose and reduce the dimension, but this obviously has a certain impact on the originality of the data.

1.2 FunkSVD(LFM)

The Traditional SVD mentioned just now needs to fill the matrix first, and then decompose and reduce the dimension. At the same time, there is a problem of high computational complexity. Because it needs to be decomposed into three matrices, funk SVD method is proposed later. Instead of decomposing the matrix into three matrices, it is decomposed into two user implicit feature and project implicit feature matrices, Funk SVD is also known as the most primitive LFM model

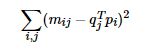
Based on the idea of linear regression, the optimal implicit vector representation of users and items is sought by minimizing the square of observation data. At the same time, in order to avoid Overfitting the observation data, FunkSVD with L2 regular term is proposed. The above formula is:

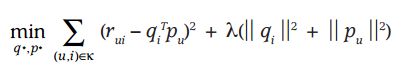
The above two optimization functions can find the optimal solution by gradient descent or random gradient descent method.

1.3 BiasSVD

After FunkSVD was proposed, there have been many modified versions. One of the relatively successful methods is BiasSVD, as the name suggests, that is, SVD decomposition with bias term:

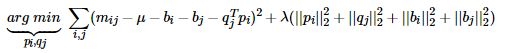
It is based on the same assumptions as the Baseline benchmark prediction, but here the Baseline bias is introduced into the matrix decomposition

SVD++:

Later, people proposed an improved BiasSVD, called SVD + +. The algorithm adds the user's implicit feedback information on the basis of BiasSVD:

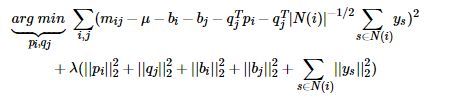
Display feedback refers to the user's rating, and implicit feedback refers to the user's browsing records, purchase records, listening records, etc.

SVD + + is based on the assumption that on the basis of BiasSVD, users' historical browsing records, purchase records and listening records of the project can reflect users' preferences from the side.

2, LFM

LFM is the Funk SVD matrix decomposition mentioned earlier

The goal of collaborative filtering with implicit semantic model

Reveal hidden features that can explain why the corresponding prediction score is given.
These features may not be described in words, but in fact we don't know, "metaphysics“

We can think that there are internal reasons why users give such scores to movies. We can dig out the hidden factors that affect users' scores, and then determine the predicted score of this non rated movie according to the correlation between the non rated movie and these hidden factors

There should be some hidden factors that affect users' scoring, such as movies: actors, themes, times... And even hidden factors that people can directly understand

Find the hidden factor and associate the user with the item (find out what makes the user like / dislike this item and what determines whether the user likes / dislikes this item), so as to infer whether the user will like a movie he has not seen

2.1 LFM principle analysis

The core idea of LFM (late factor model) implicit semantic model is to contact users and items through implicit features, as shown in the following figure:

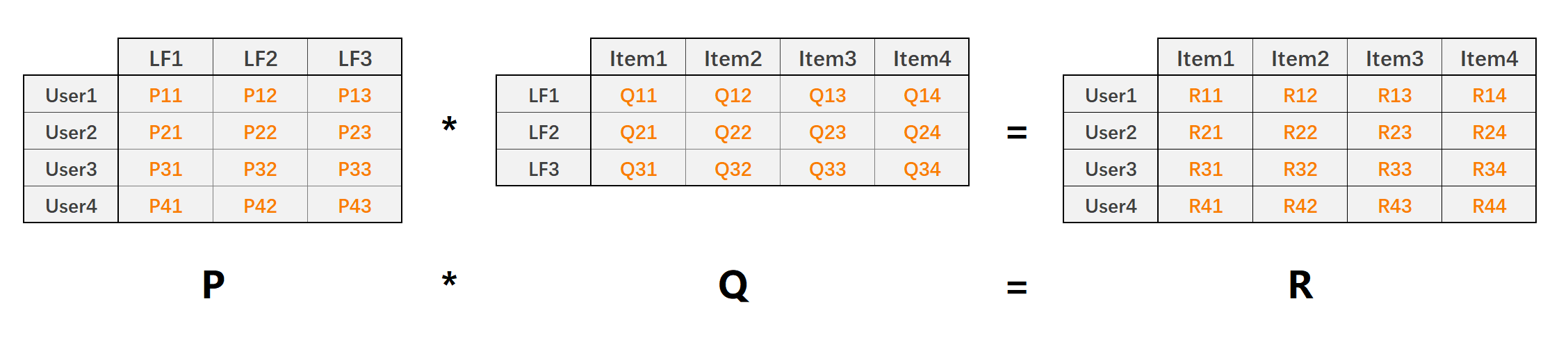
P matrix is user lf matrix, that is, user and implicit feature matrix. It can be understood as a user's preference information for each item category. LF has three, indicating that there are always three implied features.
Q matrix is lf item matrix, that is, the matrix of implied features and items, which can be understood as the information that each item belongs to each category.
R matrix is the user item matrix, which represents the user's preference information for items, which is obtained from P*Q
Can handle sparse scoring matrix

Using the matrix decomposition technology, the original user item scoring matrix (dense / sparse) is decomposed into P and Q matrices, and then the user item scoring matrix \ (R \) is restored by \ (P*Q \). The whole process is equivalent to dimensionality reduction, in which:

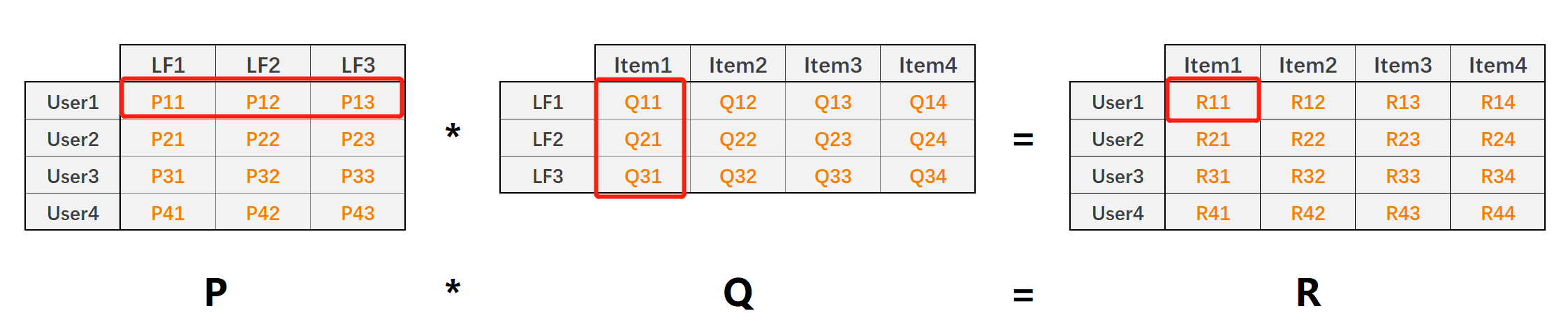
The matrix value \ (P {11} \) represents the weight value of user 1 to implicit feature 1
The matrix value \ (Q_{11} \) represents the weight value of implicit feature 1 on Article 1
The matrix value \ (R {11} \) represents the predicted score of user 1 on Item 1, and \ (R {11} = \ VEC {P {1, K}} \ cdot \ VEC {Q {K, 1} \)

LFM is used to predict the user's score on the item, and \ (k \) represents the number of implied features:

\[\begin{split} \hat {r}_{ui} &=\vec {p_{uk}}\cdot \vec {q_{ik}} \\&={\sum_{k=1}}^k p_{uk}q_{ik} \end{split} \]

Therefore, in the end, our goal is to require the P matrix and Q matrix and each value thereof, and then predict the user item score.

2.2 loss function

The prediction score matrix obtained by matrix decomposition may have errors with the known score items of the original score matrix R. our goal is to find the best decomposition method to minimize the error of the prediction score matrix after decomposition.

Similarly, for the score prediction, we use the square difference to construct the loss function:

\[\begin{split} Cost &= \sum_{u,i\in R} (r_{ui}-\hat{r}_{ui})^2 \\&=\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})^2 \end{split} \]

L2 regularization is added to prevent over fitting, λ Then we need to experiment repeatedly in the actual scene to get the appropriate value.

\[Cost = \sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})^2 + \lambda(\sum_U{p_{uk}}^2+\sum_I{q_{ik}}^2) \]

Partial derivative of loss function:

\[\begin{split} \cfrac {\partial}{\partial p_{uk}}Cost &= \cfrac {\partial}{\partial p_{uk}}[\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})^2 + \lambda(\sum_U{p_{uk}}^2+\sum_I{q_{ik}}^2)] \\&=2\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})(-q_{ik}) + 2\lambda p_{uk} \\\\ \cfrac {\partial}{\partial q_{ik}}Cost &= \cfrac {\partial}{\partial q_{ik}}[\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})^2 + \lambda(\sum_U{p_{uk}}^2+\sum_I{q_{ik}}^2)] \\&=2\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})(-p_{uk}) + 2\lambda q_{ik} \end{split} \]

2.3 optimization of stochastic gradient descent method

Gradient descent update parameter \ (p#{uk} \):

\[\begin{split} p_{uk}&:=p_{uk} - \alpha\cfrac {\partial}{\partial p_{uk}}Cost \\&:=p_{uk}-\alpha [2\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})(-q_{ik}) + 2\lambda p_{uk}] \\&:=p_{uk}+\alpha [\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})q_{ik} - \lambda p_{uk}] \end{split} \]

Similarly:

\[\begin{split} q_{ik}&:=q_{ik} + \alpha[\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})p_{uk} - \lambda q_{ik}] \end{split} \]

Random gradient descent: vector multiplication, each component is multiplied and summed

\[\begin{split} &p_{uk}:=p_{uk}+\alpha [(r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})q_{ik} - \lambda_1 p_{uk}] \\&q_{ik}:=q_{ik} + \alpha[(r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})p_{uk} - \lambda_2 q_{ik}] \end{split} \]

Because P matrix and Q matrix are two different matrices, they usually adopt different regular parameters, such as \ (\ lambda_1 \) and \ (\ lambda_2 \)

Algorithm implementation

'''
LFM Model
'''
import pandas as pd
import numpy as np

# Score prediction 1-5
class LFM(object):

    def __init__(self, alpha, reg_p, reg_q, number_LatentFactors=10, number_epochs=10, columns=["uid", "iid", "rating"]):
        self.alpha = alpha # Learning rate
        self.reg_p = reg_p    # P-matrix regularity
        self.reg_q = reg_q    # Q-matrix regularity
        self.number_LatentFactors = number_LatentFactors  # Number of implicit categories
        self.number_epochs = number_epochs    # Maximum number of iterations
        self.columns = columns

    def fit(self, dataset):
        '''
        fit dataset
        :param dataset: uid, iid, rating
        :return:
        '''

        self.dataset = pd.DataFrame(dataset)

        self.users_ratings = dataset.groupby(self.columns[0]).agg([list])[[self.columns[1], self.columns[2]]]
        self.items_ratings = dataset.groupby(self.columns[1]).agg([list])[[self.columns[0], self.columns[2]]]

        self.globalMean = self.dataset[self.columns[2]].mean()

        self.P, self.Q = self.sgd()

    def _init_matrix(self):
        '''
        initialization P and Q Matrix, and set the random value between 0 and 1 as the initial value
        :return:
        '''
        # User-LF
        P = dict(zip(
            self.users_ratings.index,
            np.random.rand(len(self.users_ratings), self.number_LatentFactors).astype(np.float32)
        ))
        # Item-LF
        Q = dict(zip(
            self.items_ratings.index,
            np.random.rand(len(self.items_ratings), self.number_LatentFactors).astype(np.float32)
        ))
        return P, Q

    def sgd(self):
        '''
        Use random gradient descent to optimize the results
        :return:
        '''
        P, Q = self._init_matrix()

        for i in range(self.number_epochs):
            print("iter%d"%i)
            error_list = []
            for uid, iid, r_ui in self.dataset.itertuples(index=False):
                # User-LF P
                ## Item-LF Q
                v_pu = P[uid] #User vector
                v_qi = Q[iid] #Item vector
                err = np.float32(r_ui - np.dot(v_pu, v_qi))

                v_pu += self.alpha * (err * v_qi - self.reg_p * v_pu)
                v_qi += self.alpha * (err * v_pu - self.reg_q * v_qi)
                
                P[uid] = v_pu 
                Q[iid] = v_qi

                # for k in range(self.number_of_LatentFactors):
                #     v_pu[k] += self.alpha*(err*v_qi[k] - self.reg_p*v_pu[k])
                #     v_qi[k] += self.alpha*(err*v_pu[k] - self.reg_q*v_qi[k])

                error_list.append(err ** 2)
            print(np.sqrt(np.mean(error_list)))
        return P, Q

    def predict(self, uid, iid):
        # If uid or iid is not available, we use the average score of the whole play as the prediction result
        if uid not in self.users_ratings.index or iid not in self.items_ratings.index:
            return self.globalMean

        p_u = self.P[uid]
        q_i = self.Q[iid]

        return np.dot(p_u, q_i)

    def test(self,testset):
        '''Predictive test set data'''
        for uid, iid, real_rating in testset.itertuples(index=False):
            try:
                pred_rating = self.predict(uid, iid)
            except Exception as e:
                print(e)
            else:
                yield uid, iid, real_rating, pred_rating

if __name__ == '__main__':
    dtype = [("userId", np.int32), ("movieId", np.int32), ("rating", np.float32)]
    dataset = pd.read_csv("datasets/ml-latest-small/ratings.csv", usecols=range(3), dtype=dict(dtype))

    lfm = LFM(0.02, 0.01, 0.01, 10, 100, ["userId", "movieId", "rating"])
    lfm.fit(dataset)

    while True:
        uid = input("uid: ")
        iid = input("iid: ")
        print(lfm.predict(int(uid), int(iid)))

3, BiasSvd

BiasSvd actually adds Bias term (Bias) on the basis of the previously mentioned Funk SVD matrix decomposition, which is the factor to measure the goods and users themselves. Reason: after observation, most of the scoring data are produced by factors unrelated to the user or the item, that is, a large part of the factors are not related to the user's preference for the item, but only depend on the characteristics of the user or the item itself. These factors that are independent of users or items are called Bias parts.

3.1 BiasSvd thought

Funk SVD method predicts by learning the feature vectors of users and items, that is, the interactive information between users and items. The user's eigenvector represents the user's interest, the item's eigenvector represents the characteristics of the item, and each dimension corresponds to each other. The inner product of the two vectors represents the user's preference for the item. However, most of the scoring data we observed are the effects of factors unrelated to users or items, that is, a large number of factors are not related to users' preferences for items, but only depend on the characteristics of users or items themselves. For example, for optimistic users, their scoring behavior is generally high, while for critical users, their scoring record is generally low. Even if they score the same item, their preference for the item is different. Similarly, for items, taking films as an example, popular films generally get high scores, while some bad films generally get low scores. These factors are independent of users or products, and have nothing to do with users' preferences for products.

We call these factors independent of users or goods as bias part, and the interaction between users and goods, that is, the user's preference for goods, as personalization part.

In fact, in the matrix decomposition model, the role of the preference part in improving the accuracy of score prediction is much higher than that of the personalized part. Taking Netflix Prize recommended competition data set as an example, Yehuda Koren can reduce the score error by 32% only by using the offset part, while adding the personalized part can reduce 42%, that is, only 10% is the role of the personalized part, This also fully illustrates the importance of the offset part. Yehuda Koren will call the remaining 58% error the unexplainable part of the model, including factors such as data noise.

3.2 objective function

The offset part is mainly composed of three sub parts:

Global average of all scoring records in the training set μ， It represents the overall score of training data. For a fixed data set, it is a constant.
User bias B \ ({u} \), a factor independent of item characteristics, indicates the scoring habits of a specific user. For example, for critical users, they are harsh on their own scores and tend to give low scores; Optimistic users give conservative scores, and the overall score is high.
Item bias B \ ({i} \), which is specific to the factors of user interest, indicates the scoring of a specific item. Taking films as an example, the overall score of good films is high, while the score of bad films is generally low. This is the characteristic of article bias capture.

Then the offset part is represented as u + B \ ({u} \) + B \ ({I} \)

Use BiasSvd to predict the user's score on the item, \ (k \) represents the number of hidden features:

\[\begin{split} \hat {r}_{ui} &=\mu + b_u + b_i + \vec {p_{uk}}\cdot \vec {q_{ki}} \\&=\mu + b_u + b_i + {\sum_{k=1}}^k p_{uk}q_{ik} \end{split} \]

3.2 loss function

Similarly, for the score prediction, we use the square difference to construct the loss function:

\[\begin{split} Cost &= \sum_{u,i\in R} (r_{ui}-\hat{r}_{ui})^2 \\&=\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i -{\sum_{k=1}}^k p_{uk}q_{ik})^2 \end{split} \]

Add L2 regularization:

\[Cost = \sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})^2 + \lambda(\sum_U{b_u}^2+\sum_I{b_i}^2+\sum_U{p_{uk}}^2+\sum_I{q_{ik}}^2) \]

Partial derivative of loss function:

\[\begin{split} \cfrac {\partial}{\partial p_{uk}}Cost &= \cfrac {\partial}{\partial p_{uk}}[\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})^2 + \lambda(\sum_U{b_u}^2+\sum_I{b_i}^2+\sum_U{p_{uk}}^2+\sum_I{q_{ik}}^2)] \\&=2\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})(-q_{ik}) + 2\lambda p_{uk} \\\\ \cfrac {\partial}{\partial q_{ik}}Cost &= \cfrac {\partial}{\partial q_{ik}}[\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})^2 + \lambda(\sum_U{b_u}^2+\sum_I{b_i}^2+\sum_U{p_{uk}}^2+\sum_I{q_{ik}}^2)] \\&=2\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})(-p_{uk}) + 2\lambda q_{ik} \end{split} \]

\[\begin{split} \cfrac {\partial}{\partial b_u}Cost &= \cfrac {\partial}{\partial b_u}[\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})^2 + \lambda(\sum_U{b_u}^2+\sum_I{b_i}^2+\sum_U{p_{uk}}^2+\sum_I{q_{ik}}^2)] \\&=2\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})(-1) + 2\lambda b_u \\\\ \cfrac {\partial}{\partial b_i}Cost &= \cfrac {\partial}{\partial b_i}[\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})^2 + \lambda(\sum_U{b_u}^2+\sum_I{b_i}^2+\sum_U{p_{uk}}^2+\sum_I{q_{ik}}^2)] \\&=2\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})(-1) + 2\lambda b_i \end{split} \]

3.3 optimization of stochastic gradient descent method

Gradient descent update parameter \ (p#{uk} \):

\[\begin{split} p_{uk}&:=p_{uk} - \alpha\cfrac {\partial}{\partial p_{uk}}Cost \\&:=p_{uk}-\alpha [2\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})(-q_{ik}) + 2\lambda p_{uk}] \\&:=p_{uk}+\alpha [\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})q_{ik} - \lambda p_{uk}] \end{split} \]

Similarly:

\[\begin{split} q_{ik}&:=q_{ik} + \alpha[\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})p_{uk} - \lambda q_{ik}] \end{split} \]

\[b_u:=b_u + \alpha[\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik}) - \lambda b_u] \]

\[b_i:=b_i + \alpha[\sum_{u,i\in R} (r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik}) - \lambda b_i] \]

Random gradient descent:

\[\begin{split} &p_{uk}:=p_{uk}+\alpha [(r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})q_{ik} - \lambda_1 p_{uk}] \\&q_{ik}:=q_{ik} + \alpha[(r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik})p_{uk} - \lambda_2 q_{ik}] \end{split} \]

\[b_u:=b_u + \alpha[(r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik}) - \lambda_3 b_u] \]

\[b_i:=b_i + \alpha[(r_{ui}-\mu - b_u - b_i-{\sum_{k=1}}^k p_{uk}q_{ik}) - \lambda_4 b_i] \]