Preface

• Language: Java
• Environment: IntelliJ IDEA
• JDK Version: 1.8
• Source code: GitHub
• Reference article: https://www.cnblogs.com/xbinworld/p/4273506.html

What is Sparse Matrix

For example, the following matrix:

Because there are so many repetitive zeros in sparse matrices, it is necessary to compress them when storing sparse matrices. Here are some commonly used sparse matrix storage formats.

Storage format

COO format

COO (Coordinate): Store only rows, columns, and values of non-zero data Although this storage method is simple, there will be repeated rows or columns, and these duplicate values need to be compressed.

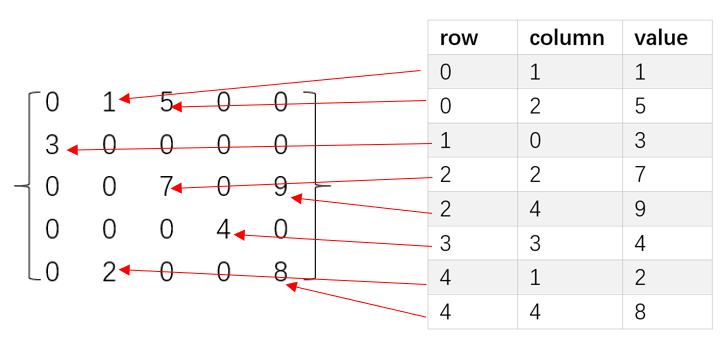
Coding process:

• compress
  1. Traversal matrix, get all non-zero data number
  2. Record the total number of rows, columns and non-zero data of the original matrix
  3. The number of compressed data rows initialized by the number of non-zero data acquired is 3, which are row, column and value, respectively.
  4. Traverse the matrix again to store the rows, columns and values of non-zero data
• decompression
  1. Initialize the original matrix with the total number of rows and columns recorded
  2. Row-by-row reduction matrix with number of non-zero data

public class COO {
    private int rows;   //Save the total number of rows of the original matrix
    private int columns;    //Preserving the total number of columns of the original matrix
    private int sum;    //Number of total valid data saved
    private int[][] data;   //Compressed data
    //Omitting get and set methods
}

public class COOUtils {
    /**
    * The original matrix is compressed by COO and the compressed data is returned.
    */
    public static COO process(int rows,int columns,int[][] source){
        COO coo = new COO();    //Data to be returned
        coo.setRows(rows);
        coo.setColumns(columns);
        int count = 0;
        for (int i = 0;i<rows;i++){ //Traverse to get the number of valid data
            for (int j = 0;j<columns;j++){
                if(source[i][j]!=0){
                    count++;
                }
             }
        }
        coo.setSum(count);
        int[][] data = new int[coo.getSum()][3];//Initialize compressed data
         int c = 0;  //Rows of mobile data
         for (int i = 0;i<rows;i++){
            for (int j = 0;j<columns;j++){
                if(source[i][j]!=0){
                    data[c][0] = i; //Assign values to row columns
                    data[c][1] = j; //Assign values to column
                    data[c][2] = source[i][j];  //Assign values to value columns
                    c++;
                }
            }
         }
        coo.setData(data);
        return coo;
     }

     /**
     * Decompress COO compressed data into original data
     */
     public static int[][] restore(COO coo){
        int[][] source = new int[coo.getRows()][coo.getColumns()];
        for (int[] row:coo.getData()){
            source[row[0]][row[1]] = row[2];
        }
        return source;
     }

     /**
     * Format and display of compressed COO data
     */
     public static String formitData(COO coo){
        int[][] data = coo.getData();
        String str = "row\tcolumn\tvalue\n";
         for (int[] row:data){
             str += row[0]+"\t"+row[1]+"\t"+row[2]+"\n";
        }
        return str;
     }

     /**
     * Format and display the original matrix
     */
     public static String formitSouce(int rows,int columns,int[][] source){
        String str = "";
        for (int i = 0;i<rows;i++){
            for (int j = 0;j<columns;j++){
                str += source[i][j]+"\t";
            }
            str += "\n";
        }
        return str;
     }
}

CSR/CSC format

CSR (Compressed Sparse Row): Columns, values, and row offsets that store only non-zero data. Row offset refers to the position of the first non-zero number of each row in the value.

CSC (Compressed Sparse Column): Only rows, values, and column offsets for non-zero data are stored. Column offset refers to the position of the first non-zero number of each column in the value.

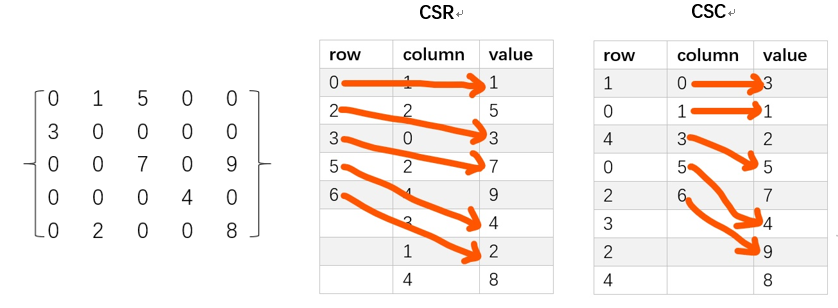
When using COO, CSR can be used to ignore rows if there are too many duplicate rows, and CSC can be used to ignore columns if there are too many duplicate columns.

Coding process:

• compress
  1. Traversal matrix, get all non-zero data number
  2. Record the total number of rows, columns and non-zero data of the original matrix
  3. Initialize the number of compressed data rows by the number of non-zero data acquired. The number of columns is 2, which are column and value, respectively.
  4. Traverse the matrix again to store the rows, columns and values of non-zero data
  5. Calculate row offset by value and store it
• decompression
  1. Initialize the original matrix with the total number of rows and columns recorded
  2. Using non-zero data number to restore the matrix row by row with the number of cycles, restoring the control rows by the recorded row offset at the same time

Row offset can be understood in decompression process as follows: ignoring the existence of rows, sequential restoring of data, the value of row offset is to wrap lines when it is looped to this value.

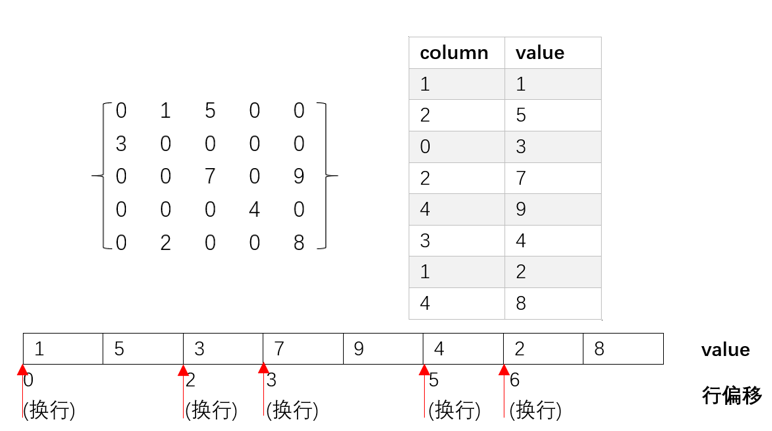
public class CSR {
    private int rows;   //Save the total number of rows of the original matrix
    private int columns;    //Preserving the total number of columns of the original matrix
    private int sum;    //Number of total valid data saved
    private int[] rowOffset;    //Preservation row migration
    private int[][] data;   //Save columns, values
    //get and set method ellipsis
}
public class CSRUtils {
    /**
    * The original matrix is compressed by CSR and the compressed data is returned.
    */
    public static CSR process(int rows,int columns,int[][] source){
        CSR csr = new CSR();    //Data to be returned
        csr.setRows(rows);
        csr.setColumns(columns);
        int count = 0;
        for (int i = 0;i<rows;i++){ //Traverse to get the number of valid data
            for (int j = 0;j<columns;j++){
                if(source[i][j]!=0){
                count++;
                }
            }
        }
        csr.setSum(count);
        int[] rowOffset = new int[csr.getRows()];//Storage row offset
        int[][] data = new int[csr.getSum()][2];//Initialize compressed data
        boolean isFirst = false;    //Mark each first number
        int f = 0;  //Index of Mobile first Array
        int[] first = new int[csr.getRows()];   //Store the first value of each row
        int[] valueOrder = new int[csr.getSum()];   //Sequential values that store all valid data
        int c = 0;  //Rows of mobile data
        for (int i = 0;i<rows;i++){
            for (int j = 0;j<columns;j++){
                if(source[i][j]!=0){
                    data[c][0] = j; //Assign values to column
                    data[c][1] = source[i][j];  //Assign values to value columns
                    valueOrder[c] = source[i][j];
                    c++;
                    if(!isFirst){   //Assign a value to the first number in each row
                        first[f] = source[i][j];
                        isFirst = true;
                    }
                }
            }
            f++;
            isFirst = false;
        }
        for (int i = 0;i<csr.getRows();i++){    //Computing row migration
            rowOffset[i] = getFirstIndex(first[i],valueOrder);
            valueOrder[rowOffset[i]] = 0;
        }
        csr.setData(data);
        csr.setRowOffset(rowOffset);
        return csr;
    }

    /**
    * Decompress the compressed CSR data into the original data
    */
    public static int[][] restore(CSR csr){
        int[][] source = new int[csr.getRows()][csr.getColumns()];
        int[][] data = csr.getData();
        int row = -1;   //Mark the current row
        int j = 0;  //Moving row offset array
        int[] rowOffset = csr.getRowOffset();
        int nowOffset = rowOffset[j];   //Get the current row offset
        for(int i = 0;i<csr.getSum();i++){
            if(nowOffset == i){ //When the row offset is equal to the position of a non-zero value in value
                if(j!=csr.getRows()-1){ //And the row offset array index cannot exceed the total number of rows
                    j++;
                    nowOffset = rowOffset[j];   //Increased current offset
                }
                row++;  //Current row increase
            }
            source[row][data[i][0]] = data[i][1];
        }
        return source;
    }

    /**
    * Format Display of Compressed CSR Data
    */
    public static String formitData(CSR csr){
        int[][] data = csr.getData();
        int [] rowOffset =csr.getRowOffset();
        String str = "row\tcolumn\tvalue\n";
        for (int i = 0;i<csr.getSum();i++){
            if(i<rowOffset.length){
                str += rowOffset[i]+"\t";
            }else{
                str += "\t";
            }
            str += data[i][0]+"\t"+data[i][1]+"\n";
        }
        return str;
    }

    /**
    * Format and display the original matrix
    */
    public static String formitSouce(int rows,int columns,int[][] source){
        String str = "";
        for (int i = 0;i<rows;i++){
            for (int j = 0;j<columns;j++){
                str += source[i][j]+"\t";
            } 
            str += "\n";
        }
        return str;
    }

    /**
    * Find the location of target in the first occurrence of array arr
    */
    private static int getFirstIndex(int target,int[] arr){
        for (int i = 0;i<arr.length;i++){
            if (target == arr[i]){
                return i;
            }
        }
        return -1;
    }
}