From: https://blog.csdn.net/liyuanbhu/article/details/38849897
-------------------------------------------
A recently written program requires an IIR filter, and the coefficients of the IIR filter need to be dynamically adjusted.Therefore, it took some time to study the implementation of IIR filters.
Previously used IIR filter parameters are pre-determined, there is a website, as long as the filter parameter characteristics are entered, you can directly generate the required C code.
http://www-users.cs.york.ac.uk/~fisher/mkfilter/trad.html
I've been lazy about using the results of this website directly, so I haven't accumulated any useful code.This time you need to start from scratch.
I have two problems:
1. Based on the filter parameters (filter type, cutoff frequency, filter order, etc.), the coefficients of the difference equation corresponding to the filter are calculated.
2. A working filter is constructed using the coefficients of the difference equation.
The first one is that for different types of filters, such as Butterworth and Bessel, the calculation methods of filter coefficients are different.I haven't done all this yet, so I'll write another article until I have implemented the coefficient calculation methods for several common filter types.
Write the second question first.The difference equation for the IIR filter is:
The corresponding system functions are:
The default here is a[0] = 1.In fact, you can always make a[0] = 1 by adjusting the values of a[k] and b[k], so this condition is always met.
As described above in Oppenheimer's Discrete Time Signal Processing, IIR filters have two basic implementations, Direct I and Direct II.I wrote two classes to implement both forms.
Direct Type I
class IIR_I
{
private:
double *m_pNum;
double *m_pDen;
double *m_px;
double *m_py;
int m_num_order;
int m_den_order;
public:
IIR_I();
void reset();
void setPara(double num[], int num_order, double den[], int den_order);
void resp(double data_in[], int m, double data_out[], int n);
double filter(double data);
void filter(double data[], int len);
void filter(double data_in[], double data_out[], int len);
};Where m_px stores the value of x[n-k] (m_px[0] stores x[n-0], m_px[1] stores x[n-1], and so on), m_py stores the value of y[n-k] (m_py[0] stores y[n-0], m_py[1] stores y[n-1], and so on).
Three filter functions are used to do the actual filtering.Before that, the setPara function is needed to initialize the filter's coefficients.
The following is the implementation code:
/** \brief Zero the internal state of the filter and preserve the coefficients of the filter
* \return
*/
void IIR_I::reset()
{
for(int i = 0; i <= m_num_order; i++)
{
m_pNum[i] = 0.0;
}
for(int i = 0; i <= m_den_order; i++)
{
m_pDen[i] = 0.0;
}
}
IIR_I::IIR_I()
{
m_pNum = NULL;
m_pDen = NULL;
m_px = NULL;
m_py = NULL;
m_num_order = -1;
m_den_order = -1;
};
/** \brief
*
* \param num Coefficient of molecule polynomial, ascending order, num[0] is a constant term
* \param m Order of Molecular Polynomial
* \param den Denominator polynomial coefficients, ascending order, den[0] is a constant term
* \param m Order of denominator polynomial
* \return
*/
void IIR_I::setPara(double num[], int num_order, double den[], int den_order)
{
delete[] m_pNum;
delete[] m_pDen;
delete[] m_px;
delete[] m_py;
m_pNum = new double[num_order + 1];
m_pDen = new double[den_order + 1];
m_num_order = num_order;
m_den_order = den_order;
m_px = new double[num_order + 1];
m_py = new double[den_order + 1];
for(int i = 0; i <= m_num_order; i++)
{
m_pNum[i] = num[i];
m_px[i] = 0.0;
}
for(int i = 0; i <= m_den_order; i++)
{
m_pDen[i] = den[i];
m_py[i] = 0.0;
}
}
/** \brief Filter function, using direct type I structure
*
* \param data Incoming Input Data
* \return Filtered results
*/
double IIR_I::filter(double data)
{
m_py[0] = 0.0; // Store filtered results
m_px[0] = data;
for(int i = 0; i <= m_num_order; i++)
{
m_py[0] = m_py[0] + m_pNum[i] * m_px[i];
}
for(int i = 1; i <= m_den_order; i++)
{
m_py[0] = m_py[0] - m_pDen[i] * m_py[i];
}
for(int i = m_num_order; i >= 1; i--)
{
m_px[i] = m_px[i-1];
}
for(int i = m_den_order; i >= 1; i--)
{
m_py[i] = m_py[i-1];
}
return m_py[0];
}
/** \brief Filter function, using direct type I structure
*
* \param data[] Input data, returned with filtered results
* \param len data[] The length of the array
* \return
*/
void IIR_I::filter(double data[], int len)
{
int i, k;
for(k = 0; k < len; k++)
{
m_px[0] = data[k];
data[k] = 0.0;
for(i = 0; i <= m_num_order; i++)
{
data[k] = data[k] + m_pNum[i] * m_px[i];
}
for(i = 1; i <= m_den_order; i++)
{
data[k] = data[k] - m_pDen[i] * m_py[i];
}
// we get the y value now
m_py[0] = data[k];
for(i = m_num_order; i >= 1; i--)
{
m_px[i] = m_px[i-1];
}
for(i = m_den_order; i >= 1; i--)
{
m_py[i] = m_py[i-1];
}
}
}
/** \brief Filter function, using direct type I structure
*
* \param data_in[] Input data
* \param data_out[] Save filtered data
* \param len The length of the array
* \return
*/
void IIR_I::filter(double data_in[], double data_out[], int len)
{
int i, k;
for(k = 0; k < len; k++)
{
m_px[0] = data_in[k];
m_py[0] = 0.0;
for(i = 0; i <= m_num_order; i++)
{
m_py[0] = m_py[0] + m_pNum[i] * m_px[i];
}
for(i = 1; i <= m_den_order; i++)
{
m_py[0] = m_py[0] - m_pDen[i] * m_py[i];
}
for(i = m_num_order; i >= 1; i--)
{
m_px[i] = m_px[i-1];
}
for(i = m_den_order; i >= 1; i--)
{
m_py[i] = m_py[i-1];
}
data_out[k] = m_py[0];
}
}
In addition, a resp function is provided, which calculates the time domain response of the filter.It is also not required that data_in and data_out have the same array length.The data before default data_in[0] is all zero, and the number after data_in[M-1] is all data_in[M-1].Therefore, only one data point is needed to calculate the step response input data with this function.And this function does not change the internal state of the filter.
/** \brief Calculates the time domain response of the IIR filter without affecting the internal state of the filter
* \param data_in For filter input, input before 0 minutes defaults to 0, data_in[M] and after defaults to data_in[M-1]
* \param data_out Output of filter
* \param M Length of input data
* \param N Length of output data
* \return
*/
void IIR_I::resp(double data_in[], int M, double data_out[], int N)
{
int i, k, il;
for(k = 0; k < N; k++)
{
data_out[k] = 0.0;
for(i = 0; i <= m_num_order; i++)
{
if( k - i >= 0)
{
il = ((k - i) < M) ? (k - i) : (M - 1);
data_out[k] = data_out[k] + m_pNum[i] * data_in[il];
}
}
for(i = 1; i <= m_den_order; i++)
{
if( k - i >= 0)
{
data_out[k] = data_out[k] - m_pDen[i] * data_out[k - i];
}
}
}
}
Direct Type II
/**< IIR Filter Direct Type II Implementation */
class IIR_II
{
public:
IIR_II();
void reset();
void setPara(double num[], int num_order, double den[], int den_order);
void resp(double data_in[], int m, double data_out[], int n);
double filter(double data);
void filter(double data[], int len);
void filter(double data_in[], double data_out[], int len);
protected:
private:
double *m_pNum;
double *m_pDen;
double *m_pW;
int m_num_order;
int m_den_order;
int m_N;
};
class IIR_BODE
{
private:
double *m_pNum;
double *m_pDen;
int m_num_order;
int m_den_order;
complex<double> poly_val(double p[], int order, double omega);
public:
IIR_BODE();
void setPara(double num[], int num_order, double den[], int den_order);
complex<double> bode(double omega);
void bode(double omega[], int n, complex<double> resp[]);
};The direct type II implementation requires much fewer storage units.In addition, the external interfaces for both implementations are identical.
IIR_II::IIR_II()
{
//ctor
m_pNum = NULL;
m_pDen = NULL;
m_pW = NULL;
m_num_order = -1;
m_den_order = -1;
m_N = 0;
};
/** \brief Zero the internal state of the filter and preserve the coefficients of the filter
* \return
*/
void IIR_II::reset()
{
for(int i = 0; i < m_N; i++)
{
m_pW[i] = 0.0;
}
}
/** \brief
*
* \param num Coefficient of molecule polynomial, ascending order, num[0] is a constant term
* \param m Order of Molecular Polynomial
* \param den Denominator polynomial coefficients, ascending order, den[0] is a constant term
* \param m Order of denominator polynomial
* \return
*/
void IIR_II::setPara(double num[], int num_order, double den[], int den_order)
{
delete[] m_pNum;
delete[] m_pDen;
delete[] m_pW;
m_num_order = num_order;
m_den_order = den_order;
m_N = max(num_order, den_order) + 1;
m_pNum = new double[m_N];
m_pDen = new double[m_N];
m_pW = new double[m_N];
for(int i = 0; i < m_N; i++)
{
m_pNum[i] = 0.0;
m_pDen[i] = 0.0;
m_pW[i] = 0.0;
}
for(int i = 0; i <= num_order; i++)
{
m_pNum[i] = num[i];
}
for(int i = 0; i <= den_order; i++)
{
m_pDen[i] = den[i];
}
}
/** \brief Calculates the time domain response of the IIR filter without affecting the internal state of the filter
* \param data_in For filter input, input before 0 minutes defaults to 0, data_in[M] and after defaults to data_in[M-1]
* \param data_out Output of filter
* \param M Length of input data
* \param N Length of output data
* \return
*/
void IIR_II::resp(double data_in[], int M, double data_out[], int N)
{
int i, k, il;
for(k = 0; k < N; k++)
{
data_out[k] = 0.0;
for(i = 0; i <= m_num_order; i++)
{
if( k - i >= 0)
{
il = ((k - i) < M) ? (k - i) : (M - 1);
data_out[k] = data_out[k] + m_pNum[i] * data_in[il];
}
}
for(i = 1; i <= m_den_order; i++)
{
if( k - i >= 0)
{
data_out[k] = data_out[k] - m_pDen[i] * data_out[k - i];
}
}
}
}
/** \brief Filter function with direct type II structure
*
* \param data Input data
* \return Filtered results
*/
double IIR_II::filter(double data)
{
m_pW[0] = data;
for(int i = 1; i <= m_den_order; i++) // Update the status of w[n] first
{
m_pW[0] = m_pW[0] - m_pDen[i] * m_pW[i];
}
data = 0.0;
for(int i = 0; i <= m_num_order; i++)
{
data = data + m_pNum[i] * m_pW[i];
}
for(int i = m_N - 1; i >= 1; i--)
{
m_pW[i] = m_pW[i-1];
}
return data;
}
/** \brief Filter function with direct type II structure
*
* \param data[] Input data, returned with filtered results
* \param len data[] The length of the array
* \return
*/
void IIR_II::filter(double data[], int len)
{
int i, k;
for(k = 0; k < len; k++)
{
m_pW[0] = data[k];
for(i = 1; i <= m_den_order; i++) // Update the status of w[n] first
{
m_pW[0] = m_pW[0] - m_pDen[i] * m_pW[i];
}
data[k] = 0.0;
for(i = 0; i <= m_num_order; i++)
{
data[k] = data[k] + m_pNum[i] * m_pW[i];
}
for(i = m_N - 1; i >= 1; i--)
{
m_pW[i] = m_pW[i-1];
}
}
}
/** \brief Filter function with direct type II structure
*
* \param data_in[] Input data
* \param data_out[] Save filtered data
* \param len The length of the array
* \return
*/
void IIR_II::filter(double data_in[], double data_out[], int len)
{
int i, k;
for(k = 0; k < len; k++)
{
m_pW[0] = data_in[k];
for(i = 1; i <= m_den_order; i++) // Update the status of w[n] first
{
m_pW[0] = m_pW[0] - m_pDen[i] * m_pW[i];
}
data_out[k] = 0.0;
for(i = 0; i <= m_num_order; i++)
{
data_out[k] = data_out[k] + m_pNum[i] * m_pW[i];
}
for(i = m_N - 1; i >= 1; i--)
{
m_pW[i] = m_pW[i-1];
}
}
}
test
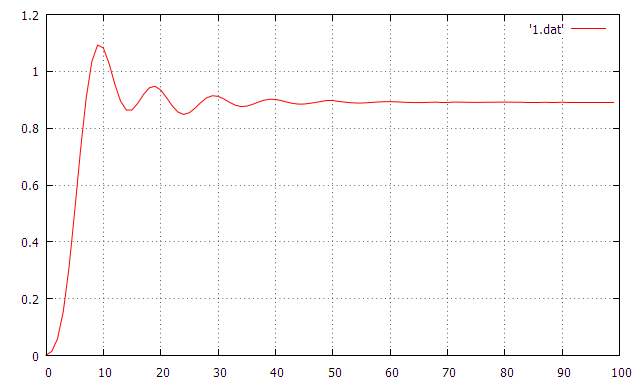
The following are some test examples. First, the step response of a fourth-order Chebyshev low-pass filter is calculated.
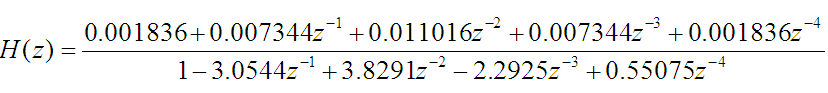
void resp_test(void)
{
double b[5] = {0.001836, 0.007344, 0.011016, 0.007344, 0.001836};
double a[5] = {1.0, -3.0544, 3.8291, -2.2925, 0.55075};
double x[2] = {1.0, 1.0};
double y[100];
IIR_II filter;
filter.setPara(b, 4, a, 4);
filter.resp(x, 2, y, 100);
for(int i= 0; i< 100; i++)
{
cout << y[i] << endl;
}
}The results are as follows:
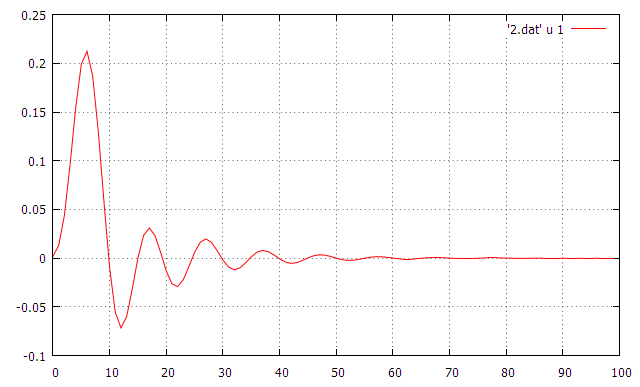
This same filter calculates the result when the input signal is a delta function.
void filter_test(void)
{
double b[5] = {0.001836, 0.007344, 0.011016, 0.007344, 0.001836};
double a[5] = {1.0, -3.0544, 3.8291, -2.2925, 0.55075};
double x[100], y[100];
int len = 100;
IIR_I filter;
//IIR_II filter;
filter.setPara(b, 4, a, 4);
for (int i = 0; i < len; i++)
{
x[i] = 0.0;
y[i] = 0.0;
}
x[0] = 1.0;
filter.filter(x, y, 100);
filter.reset();
filter.filter(x, 100);
for (int i = 0; i < len; i++)
{
cout << x[i] <<", " << y[i]<< endl;
}
}
The results are as follows:
---------------------
Author: liyuanbhu
Source: CSDN
Original: https://blog.csdn.net/liyuanbhu/article/details/38849897
Copyright Statement: This is an original article of the blogger. Please attach a link to the blog post to reproduce it!