1, Algorithm principle
1. Reference papers
Sweet rain, Yang Yu Improved Patchwork watermarking algorithm based on transform domain [J] Journal of Chengdu University of information engineering, 2017,32 (06): 623-627
2. Theoretical basis
(1) Discrete cosine transform
In the watermarking algorithm, the transform domain of the image is introduced to embed the watermark, so as to enhance the transparency of the watermark.
(2) Characteristics of human visual system
The human visual system is sensitive to different colors. According to the brightness equation y = 0.299r + 0.587G+0.144B, human eyes are most sensitive to green light, followed by red light, and least sensitive to blue light. The sum of the sensitivity of human eyes to red light and blue light is close to that to green light. In this paper, the red and blue light parts are used as the A set of Pacthwork algorithm and the green light is used as the B set. The two sets use the opposite operation when embedding information, which can offset the visual changes of the image caused by the embedded information to A certain extent and improve the transparency of the watermark.
3. Specific algorithm
(1) Watermark embedding
1) Image preprocessing
The carrier image I and watermark image w select a square R GB image, and meet the requirement that the side length of the carrier image is a multiple of 8, and the side length of the carrier image is 8 times that of the watermark image. Separate the three color channels of the carrier image I to obtain three color components: IR, IG and IB; The three color channels of the watermark image W are separated to obtain three color components WR, WG and WB.
2) Arnold permutation of watermark
Arnold transform the three color components of WR, WG and WB. The transformation process can be regarded as the process of stretching, compression, folding and splicing. After transformation, WRA, WGA and WBA are obtained. Arnold transformation process is as follows:
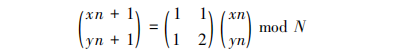
Where (x,y) is the point coordinate on the image.
3) DCT transform the carrier image and extract the DC component.
Each component of the carrier image is represented by 8 × The size of 8 is a unit and divided into several sub blocks. Treat the sub block as a whole. The position coordinates of the sub block in the top left corner are (1,1), and the position coordinates of the adjacent sub block on the right are (1,2), and so on. Apply DCT transformation to each sub block respectively, and then take out the DC component in the upper left corner of each sub block after transformation to form a new matrix. The DC component of the sub block with position coordinate (1,1) is used as the element of the position of the new matrix (1,1), and the DC component of the sub block with position coordinate (1,2) is used as the element of the position of the new matrix (1,2), and so on. The resulting matrix is called DC component matrix IRD, IBD and IGD.
4) Embedding watermark in DC component matrix
The watermark is embedded in the DC component matrix by adding / subtracting the brightness of the scrambled watermark image component k times. The component extraction formula is as follows:
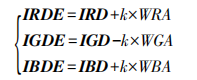
The green component uses the subtraction operation in brightness processing, and the red component and blue component use the addition operation. According to the characteristics of human visual system, these two inverse operations can offset the visual changes of the image caused by the embedded information to a certain extent, and improve the transparency of the watermark.
5) Composite embedded watermark image
After embedding the watermark, the DC component matrices IRDE, IBDE and IGDE replace the DC component of each sub block according to the corresponding position, and then apply the inverse DCT transform to each sub block to complete the watermark embedding of each color component.
Finally, the three components are synthesized into a watermark image.
(2) Watermark extraction
1) Pretreatment
Separate the three color channels of the carrier image P containing digital watermark to obtain three color components: PR, PG and Pb; The three color channels of the original carrier image I are separated to obtain three color components: IR, IG and IB.
2) Block DCT transform the image containing watermark and extract the DC component
For the carrier image P with watermark, the same DC component extraction method as that during watermark embedding is used to obtain PRD, PBD and PGD.
3) Extracting scrambled watermark from DC component matrix
The extraction method is as follows:
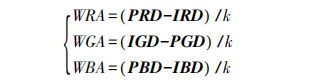
The three components are combined into the extracted watermark after inverse Arnold transform.
2, Algorithm implementation
1. Code display (matlab 2018)
%% initialization
clc;
clear ;
figure(1); %open windows
%% Load data
I=imread("I.png");
%I=imresize(I,[512,512],'nearest');
subplot( 2,2,1) ,imshow(I),title('Carrier image');
W=imread("W.png");
%W=imresize(W,[64,64],'nearest');
subplot(2,2,2),imshow(W),title('Watermark image');
[row,col,t] = size(W);
%% Embedded watermark part
%separate R,G,B passageway
IR=I(:,:,1);
IG=I(:,:,2);
IB=I(:,:,3);
WR=W(:,:,1);
WG=W(:,:,2);
WB=W(:,:,3);
%set up k,Different pictures k Different values
k=0.162;
%% use Arnold Transform scrambling watermark
WRA=arnold(WR,1,1,1);
WRA=double(WRA);
WGA=arnold(WG,1,1,1);
WGA=double(WGA);
WBA=arnold(WB,1,1,1);
WBA=double(WBA);
%%
% The carrier image is 8*8 Block processing, and then separate each block DCT change
IRD=blkproc(IR,[8,8],'dct2');
IGD=blkproc(IG,[8,8],'dct2');
IBD=blkproc(IB,[8,8],'dct2');
IRDE=IRD;
IGDE=IGD;
IBDE=IBD;
%% Extract DC component,The watermark is embedded into the matrix
for i=0:(row-1)
for j=0:(col-1)
x=i*8;
y=j*8;
IRDE(x+1,y+1)=IRD(x+1,y+1)+k*WRA(i+1,j+1);
IBDE(x+1,y+1)=IBD(x+1,y+1)+k*WBA(i+1,j+1);
IGDE(x+1,y+1)=IGD(x+1,y+1)-k*WGA(i+1,j+1);
end
end
%% Block inversion of carrier image DCT Transform
IR2=blkproc(IRDE,[8,8],'idct2');
IG2=blkproc(IGDE,[8,8],'idct2');
IB2=blkproc(IBDE,[8,8],'idct2');
IR2=uint8(IR2);
IG2=uint8(IG2);
IB2=uint8(IB2);
%% synthesis
I_embed = I;
I_embed(:,:,1) = IR2;
I_embed(:,:,2) = IG2;
I_embed(:,:,3) = IB2;
subplot( 223) ,imshow(I_embed),title('Carrier image after embedding watermark');
%% Extracting watermark
%% Separation channel
P=I_embed;
PR=P(:,:,1);
PG=P(:,:,2);
PB=P(:,:,3);
%% The watermarked image is processed DCT Transform
PRD=blkproc(PR,[8,8],'dct2');
PGD=blkproc(PG,[8,8],'dct2');
PBD=blkproc(PB,[8,8],'dct2');
WR2=WR;
WB2=WB;
WG2=WG;
%% Watermark extraction
for i=0:(row-1)
for j=0:(col-1)
x=i*8;
y=j*8;
WR2(i+1,j+1)=(PRD(x+1,y+1)-IRD(x+1,y+1))/k;
WB2(i+1,j+1)=(PBD(x+1,y+1)-IBD(x+1,y+1))/k;
WG2(i+1,j+1)=(IGD(x+1,y+1)-PGD(x+1,y+1))/k;
end
end
%% inverse arnold
WR2=uint8(WR2);
WG2=uint8(WG2);
WB2=uint8(WB2);
WR2=rearnold(WR2,1,1,1);
WG2=rearnold(WG2,1,1,1);
WB2=rearnold(WB2,1,1,1);
%% Synthetic watermark
W2=W;
W2(:,:,1)=WR2;
W2(:,:,2)=WG2;
W2(:,:,3)=WB2;
subplot( 224) ,imshow(W2),title('Extracted watermark');
imwrite(I_embed,'I_embed.png');
imwrite(W2,'W2.png');
%% arnold Transform
function arnoldImg = arnold(img,a,b,n)
[h,w] = size(img);
N=h;
arnoldImg = zeros(h,w);
for i=1:n
for y=1:h
for x=1:w
%To prevent errors in the remainder taking process, first transform the coordinate system from 0 to N-1
xx=mod((x-1)+b*(y-1),N)+1;
yy=mod(a*(x-1)+(a*b+1)*(y-1),N)+1;
arnoldImg(yy,xx)=img(y,x);
end
end
img=arnoldImg;
end
arnoldImg = uint8(arnoldImg);
end
function img = rearnold(arnoldImg,a,b,n)
[h,w] = size(arnoldImg);
img = zeros(h,w);
N = h;
for i=1:n
for y=1:h
for x=1:w
xx=mod((a*b+1)*(x-1)-b*(y-1),N)+1;
yy=mod(-a*(x-1)+(y-1),N)+1 ;
img(yy,xx)=arnoldImg(y,x);
end
end
arnoldImg=img;
end
img = uint8(img);
end
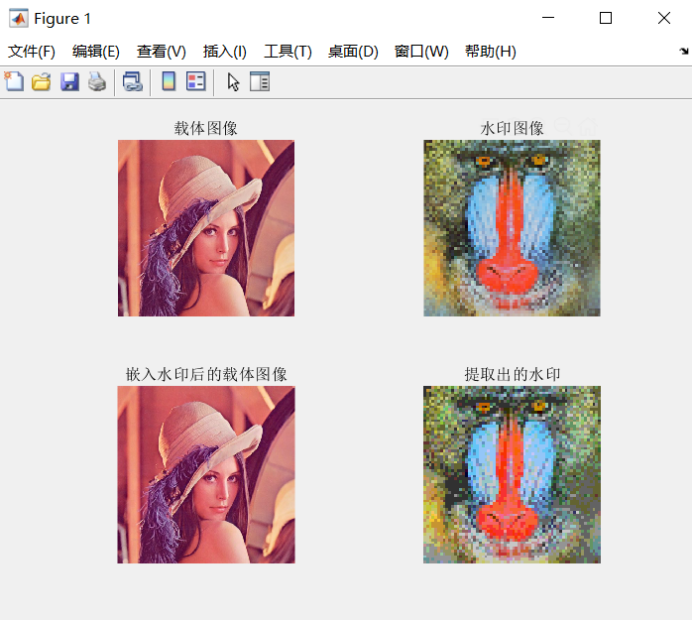
2. Realization effect
The effect of the algorithm is as follows:
3. Algorithm evaluation
(1) Concealment
Intuitively, it can be found that the difference between the images embedded in the carrier and before the carrier cannot be distinguished by the naked eye, but there is a certain distortion between the extracted watermark image and the raw water seal.
After calculation, the peak signal-to-noise ratio of the image after embedding the carrier and the image before embedding the carrier is 50.454, the correlation number is 0.9919, and the correlation number between the extracted watermark image and the original image is 0.9944.
(2) Capacity
In terms of capacity, assuming that the carrier image size of the algorithm is mm, the watermark image can be (m/8)(m/8).
(3) Robustness
1) jpeg compression attack
The compressed image and the extracted watermark are as follows:

The correlation number between the watermark extracted after the attack and the raw water seal is 0.913
2) Amplification attack
The attack first enlarges the image by 2x and then shrinks it by 2x
Watermark image extracted after attack

The correlation number between the watermark extracted after the attack and the raw water seal is 0.9836
3) Shrink attack
The attack reduces the image by 2x and then enlarges it by 2x
Watermark image extracted after attack

The correlation number between the watermark extracted after the attack and the raw water seal is 0.8195
4) Clipping attack
Cut out 25% of the area in the center of the picture.
The carrier image after attack and the extracted watermark image are as follows

The correlation number between the watermark extracted after the attack and the raw water seal is 0.8547
5) Gaussian filtering attack
Gaussian filtering for carrier image

The correlation number between the watermark extracted after the attack and the raw water seal is 0.9434
From the above experimental results, it can be seen that the algorithm has certain robustness.
3, Steganalysis
1. Attack premise
The attacker only has the watermark image, but the attacker knows that the steganography method is patchwork class and its extension
2. Analytical method
The gray image of each component of the picture is extracted and classified. Because the three channels of the normal picture have not been transformed, it is different from the picture after loading the watermark