The following describes the implementation of knapsack, queue and stack (based on array), which is a partial summary of section 1.3 of algorithm (Fourth Edition).

API is the starting point of development, so the API is given first:

Table 1 API of generic iteratable base set data type

The general idea is to give a simple and classic implementation, then discuss its improvement, and get all the implementations of the API in Table 1.

Constant volume stack

To start with, we first implement an abstract data type that represents a fixed capacity string stack, as shown in Table 2.

Its API is different from Stack's API: it can only handle String values. It requires the use case to specify a capacity and does not support iteration. The first step in implementing an API is to select the representation of data. For FixedCapacityStackOfStrings, we can obviously choose a String array. From this, we can get the implementation at the bottom of Table 2.

Table 2 an abstract data type representing constant volume string stack Table 3 track of test cases of fixedcapacitystackofstrings

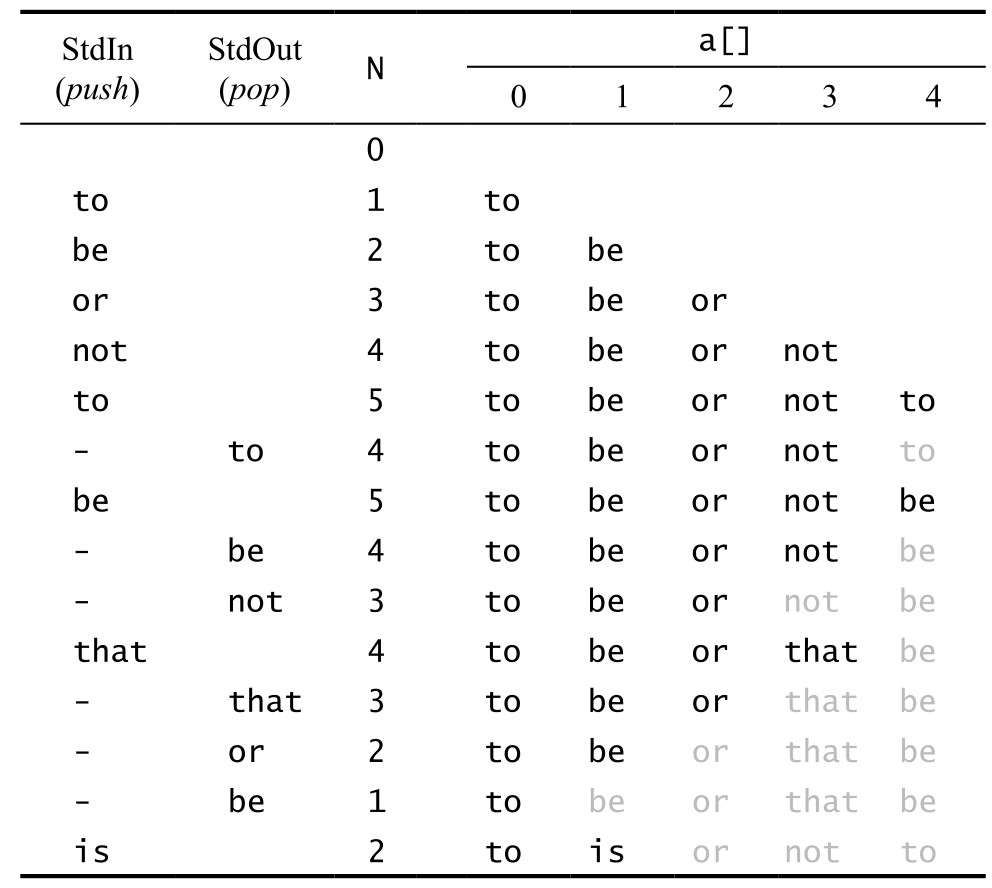
The main performance feature of this implementation is that the time required for push and pop operations is independent of the length of the stack. Many applications choose it because of its simplicity. However, several shortcomings limit its potential as a general tool. Let's try to improve it.

Generic constant volume stack

The first disadvantage of FixedCapacityStackOfStrings is that it can only handle String objects. In this regard, we can introduce generics into our code (for an introduction to generics, see Take a quick look at Java generics ). The code in Table 4 shows the details of the implementation.

Table 4 an abstract data type representing generic constant volume stack

Resize array

In Java, once the array is created, its size cannot be changed, so the space used by the stack can only be part of the maximum capacity. Creating a large stack wastes a lot of memory when the stack is empty or almost empty. The stack with small capacity may not meet the requirements of saving a large amount of data.

Therefore, it is better for FixedCapacityStack to support dynamic resizing of the array, so that it is enough to save all elements without wasting too much space.

To do this, we can add a resize(int) method.

private void resize(int max)
{	// Move the stack with size n < = max to a new array with size max
	Item[] temp = (Item[]) new Object[max];
	for (int i = 0; i < N; i++)
		temp[i] = a[i];
	a = temp;
}

Then in push(), check whether the array is too small. If it is too small, increase the length of the array.

public void push(Item item)
{	// Push elements into the top of the stack
	if (N == a.length) resize(2*a.length);
	a[N++] = item;
}

Similarly, in pop(), the element at the top of the stack is deleted first, and then if the array is too large, we will halve its length.

public Item pop()
{	// Delete element from top of stack
	Item item = a[--N];
	a[N] = null;  // Avoid object drift
	if (N > 0 && N == a.length/4) resize(a.length/2);
	return item;
}

The track of array size adjustment in push() and pop() operations is shown in Table 5.

Table 5 track of array sizing in a series of push() and pop() operations

iteration

One of the basic operations of a collection class data type is the ability to iterate through and process each element in the collection using Java's foreach statement. For methods of adding iterations to your code, see Java iteratable data types.

Implementation of stack

With the previous preparation, we can write the implementation of pressing down the stack and dynamically adjusting the size of the array.

Implementation of stack (based on array)

import java.util.Iterator;
public class ResizingArrayStack<Item> implements Iterable<Item>
{
	private Item[] a = (Item[]) new Object[1];  // Stack element
	private int N = 0;                          // Number of elements
	public boolean isEmpty()  {  return N == 0; }
	public int size()         {  return N;      }
	private void resize(int max)
	{	// Move the stack to a new array of size max
		Item[] temp = (Item[]) new Object[max];
		for (int i = 0; i < N; i++)
			temp[i] = a[i];
		a = temp;
	}
	public void push(Item item)
	{	// Add element to top of stack
		if (N == a.length) resize(2*a.length);
		a[N++] = item;
	}
	public Item pop()
	{	// Delete element from top of stack
		Item item = a[--N];
		a[N] = null;  // Avoid object dissociation (see section 1.3.2.4)
		if (N > 0 && N == a.length/4) resize(a.length/2);
		return item;
	}
	public Iterator<Item> iterator()
	{  return new ReverseArrayIterator();  }
	private class ReverseArrayIterator implements Iterator<Item>
	{	// Last in first out iterations are supported
		private int i = N;
		public boolean hasNext() {  return i > 0;    }
		public    Item next()    {  return a[--i];   }
		public    void remove()  {                   }
	}
}

Implementation of knapsack and queue

Inspired by the implementation process of the above stack, we can write the implementation of knapsack and queue.

For the knapsack, change the method name of the push(Item) method in the stack implementation to add and delete the method of adding elements.

Implementation of knapsack (based on array)

import java.util.Iterator;
public class ResizingArrayBag<Item> implements Iterable<Item>
{
	private Item[] a = (Item[]) new Object[1];  // Backpack element
	private int N = 0;                          // Number of elements
	public boolean isEmpty()  {  return N == 0; }
	public int size()         {  return N;      }
	private void resize(int max)
	{	// Move the stack to a new array of size max
		Item[] temp = (Item[]) new Object[max];
		for (int i = 0; i < N; i++)
			temp[i] = a[i];
		a = temp;
	}
	public void add(Item item)
	{	// Add element to backpack
		if (N == a.length) resize(2*a.length);
		a[N++] = item;
	}
	public Iterator<Item> iterator()
	{  return new ReverseArrayIterator();  }
	private class ReverseArrayIterator implements Iterator<Item>
	{	// Support LIFO iteration
		private int i = N;
		public boolean hasNext() {  return i > 0;    }
		public    Item next()    {  return a[--i];   }
		public    void remove()  {                   }
	}
}

For queues, two instance variables can be used as indexes. One variable head points to the beginning of the queue and the other variable tail points to the end of the queue, as shown in Table 6. When deleting an element, use head to access it and add 1 to head; When inserting an element, use tail to save it and add 1 to tail. If an index crosses the boundary of the array after increasing, it is reset to 0.

Table 6 track of test cases of resizingarrayqueue

The following is the implementation of ResizingArrayQueue.

Implementation of queue (based on array)

import java.util.Iterator;
public class ResizingArrayQueue<Item> implements Iterable<Item> {
	private static final int INIT_CAPACITY = 8;
	private Item[] a = (Item[]) new Object[INIT_CAPACITY];
	private int N = 0;
	private int head = 0;
	private int tail = 0;
	public boolean isEmpty() { return N == 0; }
	public int size() { return N; }
	private void resize(int max) {
		Item[] temp = (Item[]) new Object[max];
		for (int i = 0; i < N; i++) temp[i] = a[(head + i) % a.length];
		a = temp;
		head = 0;
		tail = N;
	}
	public void enqueue(Item item) {
		if (N == a.length) resize(2 * a.length);
		a[tail++] = item;
		if (tail == a.length) tail = 0;
		N++;
	}
	public Item dequeue() {
		Item item = a[head];
		a[head++] = null;
		if (head == a.length) head = 0;
		N--;
		if (N > 0 && N == a.length / 4) resize(a.length / 2);
		return item;
	}
	public Iterator<Item> iterator() {
		return new ResizingArrayQueueIterator();
	}
	private class ResizingArrayQueueIterator
			implements Iterator<Item> {
		private int i = 0;
		public boolean hasNext() { return i < N; }
		public Item next() {
			Item item = a[(i + head) % a.length];
			i++;
			return item;
		}
	}
}