Implementation of Koch fractal snowflake based on OpenGL

I took a course in computer graphics this semester. I wanted to study hard, but... I always feel that the teacher's teaching level is limited. I didn't learn anything in a semester. At most, I was familiar with the realization of some effects in several practical assignments. Only a little bit harvest is the first assignment, the teacher asked to achieve a fractal graphics, the best is snow. It's also the first small function that I didn't realize with the tutorial after I started to learn graphics. It's realized through my own understanding and attempt of API. Although it's very simple, it's also a little progress on the way to study. Record it here (by the way, put the code up to save the hard disk of the computer, and the code itself is not much, and I don't want to put it on GitHub)

What is fractal

I wanted to write a definition carefully, but it seems that the strict definition is a little complicated... I'm lazy, so I won't write. In short, the fractal graph is based on a "parent graph" and derives a "child graph" from the "parent graph" according to a certain rule, and continues to cycle on this basis. Put a simple legend to know (Baidu directly looks for, invades and deletes):

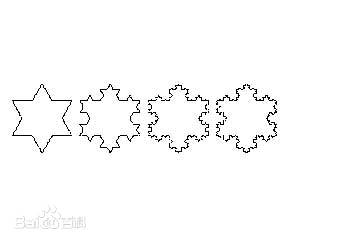
This graph should be able to better show the concept of fractal snowflake.

Implementation ideas

From the evolution of graphics, we can easily think of the idea of using recursion. Now we should consider the construction of recursion function - what is the recursion parameter? How to call the next recursion?

Obviously, if we directly take "snowflake" as the recursive object, this recursive function is difficult to realize. Through observation, we can find that in fact, the so-called "snowflake fractal" is also the fractal of line segments in essence, that is, the following figure:

Each level of fractal "snowflake" is composed of a corresponding number of "line segments", and "Fractal" is actually the fractal of all line segments once, so we only need to implement (1) - > (2) in the figure above recursively every time, the basic structure of our recursive function is: the input parameters are two endpoints (positions) of a line segment, and the internal calculation of the function needs to generate There are three endpoints (location), i.e. the endpoint at 1 / 3 of the segment, the endpoint at 2 / 3 of the segment, and the triangle vertex calculated by the two points. The implementation code of the algorithm is as follows:

aPoint v1 = mix(a, b, 1.0f / 3.0f);
aPoint v3 = mix(a, b, 2.0f / 3.0f);
aPoint v2 = caculatev2(v1, v3);

aPoint mix(aPoint a, aPoint b, float length)
{
	aPoint v;
	v.x = a.x + (b.x - a.x) * length;
	v.y = a.y + (b.y - a.y) * length;
	v.z = 0.0f;
	return v;
}

aPoint caculatev2(aPoint a, aPoint b)
{
	aPoint v;
	v.x = b.x - a.x;
	v.y = b.y - a.y;
	v.z = 0.0f;
	aPoint v2;
	v2.x = v.x * cos(glm::radians(60.0f)) - v.y * sin(glm::radians(60.0f));
	v2.y = v.x * sin(glm::radians(60.0f)) + v.y * cos(glm::radians(60.0f));
	v2.x += a.x;
	v2.y += a.y;
	v2.z = 0.0f;
	return v2;
}

A point is a structure I wrote by myself. v1 is the point 1 / 3 on the left, v2 is the prominent vertex, and v3 is the point 1 / 3 on the right. The left and right 1 / 3 points are easy to calculate, and the middle salient point is a bit troublesome. However, as long as we can push the sin/cos trigonometric functions, we will not go into details here.

Now, the calculated three points and the two endpoints of the original line segment have a total of five points, forming a new set of recursive call parameters. According to the line segment route, we take any two adjacent points in the five points as new recursive parameters (a total of four calls to the next level of recursion), as follows:

void dividLine(aPoint a, aPoint b, int Depth)
{
	if (Depth == 0)
	{
		//End recursion
	}
	else
	{
		aPoint v1 = mix(a, b, 1.0f / 3.0f);
		aPoint v3 = mix(a, b, 2.0f / 3.0f);
		aPoint v2 = caculatev2(v1, v3);
		dividLine(a, v1, Depth - 1);
		dividLine(v1, v2, Depth - 1);
		dividLine(v2, v3, Depth - 1);
		dividLine(v3, b, Depth - 1);
	}
}

When the recursion is over, we get all the vertices of Koch fractal snowflake at the corresponding recursion level. Next, we can transfer the vertices to vertex shaders and draw our snowflake by calling OpenGL functions such as glBufferData()

A difficult point

But there is a problem in the above implementation process: when OpenGL vertex shader processes vertices, it is sequential execution, which means that the vertices generated in the fractal process must be inserted into the array to be passed in order, so we can not determine the size of the array, and it is also very troublesome to insert data into the array (although vector can be used, it is also difficult to It's troublesome), and I pass all the vertices to GPU at one go. I don't know how to set the glDrawArrays() function to draw the snowflake correctly (it's not right to set the function to GL? Triangle, GL? Lines. If you are interested, you can try it). At that time, I was stuck in this place in the process of implementation. Later, I thought carefully that I could make use of recursion, because every time I recurse to the deepest level (i.e. Depth == 0), it means that the line segment composed of the two endpoints of the current input parameters will not continue to fractal, but will be drawn directly on the screen. Instead of drawing the whole snowflake in one breath, it's better to When the Depth is determined to be equal to 0, draw a line segment, so that when the whole recursion ends, the whole snowflake will be drawn automatically. In the process of querying the API, I found that before glBufferData transfers the output to the video memory, it will first clear the video memory content, and only retain the data to be transferred from the current glBufferData. With this feature, each time (Depth == 0), we can pass the positions of the current two endpoints into the display memory, and directly call the glDrawArrays() function (set to GL? Lines) to draw the line segments, so our recursive function becomes as follows:

void dividLine(aPoint a, aPoint b, int Depth)
{
	if (Depth == 0)
	{
		float vertices[] = {
			a.x, a.y, a.z, 1.0f, 1.0f, 1.0f,
			b.x, b.y, b.z, 0.0f, 0.0f, 0.0f,
		};
		glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), &vertices, GL_DYNAMIC_DRAW);
		glDrawArrays(GL_LINES, 0, 2);
	}
	else
	{
		aPoint v1 = mix(a, b, 1.0f / 3.0f);
		aPoint v3 = mix(a, b, 2.0f / 3.0f);
		aPoint v2 = caculatev2(v1, v3);
		dividLine(a, v1, Depth - 1);
		dividLine(v1, v2, Depth - 1);
		dividLine(v2, v3, Depth - 1);
		dividLine(v3, b, Depth - 1);
	}
}

experimental result

The final generation result is shown in the figure below

When the initial Depth = 1:

When the initial Depth = 2: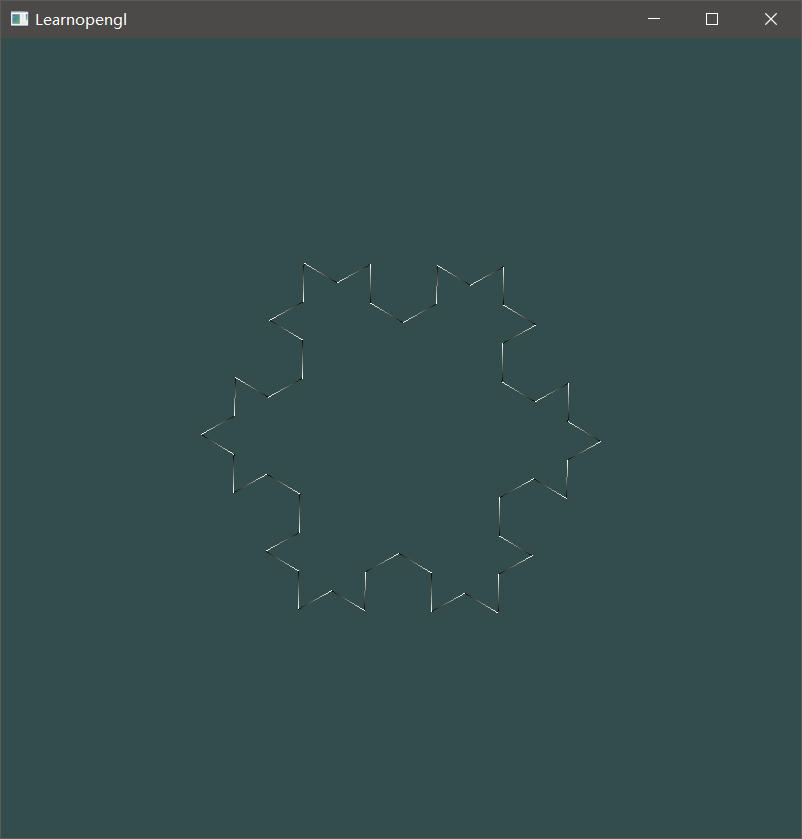

When the initial Depth = 3: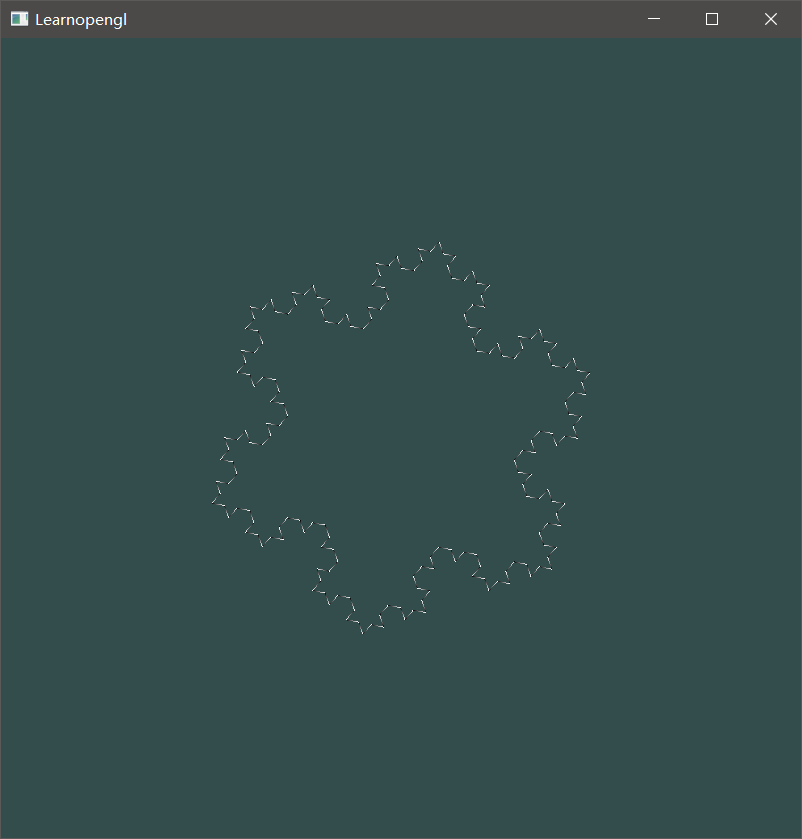

The position and direction of snowflakes in the above figure are different because our operation requirements also include the rotation and displacement of snowflakes. The complete code is as follows (including shaders):

#include <glad/glad.h>
#include <Glfw/glfw3.h>
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

#include <iostream>
#include <cmath>

const char* vertexShaderSource = "#version 330 core\n"
"layout (location = 0) in vec3 aPos;\n"
"layout (location = 1) in vec3 aColor;\n"
"out vec3 ourColor;\n"
"uniform mat4 transform;\n"
"void main()\n"
"{\n"
"	gl_Position = transform * vec4(aPos, 1.0f);\n"
"	ourColor = aColor;\n"
"}\0";

const char* fragmentShaderSource = "#version 330 core\n"
"out vec4 FragColor;\n"
"in vec3 ourColor;\n"
"void main()\n"
"{\n"
"	FragColor = vec4(ourColor, 1.0f);\n"
"}\n\0";

const int WIDTH = 800;
const int HEIGH = 800;

int direction = 1;
float speed = 1.0f;
int depth = 1;
bool leftkeytable = false;
bool rightkeytable = false;
bool leftButtonMouse = false;
double Xtranslate = 0.0f;
double Ytranslate = 0.0f;

typedef struct Point {
	float x;
	float y;
	float z;
}aPoint;

void framebuffer_size_callback(GLFWwindow* window, int width, int heigh)
{
	glViewport(0, 0, 800, 800);
}

void processInput(GLFWwindow* window)
{
	if (glfwGetKey(window, GLFW_KEY_ESCAPE) == GLFW_PRESS)
		glfwSetWindowShouldClose(window, true);
	if (glfwGetKey(window, GLFW_KEY_LEFT) == GLFW_PRESS)
	{
		leftkeytable = true;
	}
	if (glfwGetKey(window, GLFW_KEY_LEFT) != GLFW_PRESS && leftkeytable)
	{
		leftkeytable = false;
		depth--;
		if (depth < 0)
			depth = 0;
	}
	if (glfwGetKey(window, GLFW_KEY_RIGHT) == GLFW_PRESS)
	{
		rightkeytable = true;
	}
	if (glfwGetKey(window, GLFW_KEY_RIGHT) != GLFW_PRESS && rightkeytable)
	{
		rightkeytable = false;
		depth++;
		if (depth > 5)
			depth = 5;
	}
	if (glfwGetKey(window, GLFW_KEY_A) == GLFW_PRESS)
	{
		direction = 1;
	}
	if (glfwGetKey(window, GLFW_KEY_D) == GLFW_PRESS)
	{
		direction = -1;
	}
	if (glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS)
	{
		speed += 0.1f;
		if (speed > 3.0f)
			speed = 3.0f;
	}
	if (glfwGetKey(window, GLFW_KEY_S) == GLFW_PRESS)
	{
		speed -= 0.1f;
		if (speed < 0.5f)
			speed = 0.5f;
	}
	if (glfwGetMouseButton(window, GLFW_MOUSE_BUTTON_LEFT) == GLFW_PRESS)
	{
		double X, Y;
		glfwGetCursorPos(window, &X, &Y);
		Xtranslate = (X - WIDTH / 2.0) / 800.0;
		Ytranslate = (HEIGH / 2.0 - Y) / 800.0;
	}
}

aPoint mix(aPoint a, aPoint b, float length)
{
	aPoint v;
	v.x = a.x + (b.x - a.x) * length;
	v.y = a.y + (b.y - a.y) * length;
	v.z = 0.0f;
	return v;
}

aPoint caculatev2(aPoint a, aPoint b)
{
	aPoint v;
	v.x = b.x - a.x;
	v.y = b.y - a.y;
	v.z = 0.0f;
	aPoint v2;
	v2.x = v.x * cos(glm::radians(60.0f)) - v.y * sin(glm::radians(60.0f));
	v2.y = v.x * sin(glm::radians(60.0f)) + v.y * cos(glm::radians(60.0f));
	v2.x += a.x;
	v2.y += a.y;
	v2.z = 0.0f;
	return v2;
}

void dividLine(aPoint a, aPoint b, int Depth)
{
	if (Depth == 0)
	{
		float vertices[] = {
			a.x, a.y, a.z, 1.0f, 1.0f, 1.0f,
			b.x, b.y, b.z, 0.0f, 0.0f, 0.0f,
		};
		glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), &vertices, GL_DYNAMIC_DRAW);
		glDrawArrays(GL_LINES, 0, 2);
	}
	else
	{
		aPoint v1 = mix(a, b, 1.0f / 3.0f);
		aPoint v3 = mix(a, b, 2.0f / 3.0f);
		aPoint v2 = caculatev2(v1, v3);
		dividLine(a, v1, Depth - 1);
		dividLine(v1, v2, Depth - 1);
		dividLine(v2, v3, Depth - 1);
		dividLine(v3, b, Depth - 1);
	}
}

int main()
{
	glfwInit();
	glfwWindowHint(GLFW_CONTEXT_VERSION_MAJOR, 3);
	glfwWindowHint(GLFW_CONTEXT_VERSION_MINOR, 3);
	glfwWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_CORE_PROFILE);

	GLFWwindow* window = glfwCreateWindow(800, 800, "Learnopengl", nullptr, nullptr);
	if (window == nullptr)
	{
		std::cout << "Failed to create window!" << std::endl;
		glfwTerminate();
		return -1;
	}
	glfwMakeContextCurrent(window);

	if (!gladLoadGLLoader((GLADloadproc)glfwGetProcAddress))
	{
		std::cout << "Failed to initialize GLAD" << std::endl;
		return -1;
	}

	glfwSetFramebufferSizeCallback(window, framebuffer_size_callback);

	unsigned int vertexShader = glCreateShader(GL_VERTEX_SHADER);
	glShaderSource(vertexShader, 1, &vertexShaderSource, NULL);
	glCompileShader(vertexShader);

	int success;
	char infoLog[512];
	glGetShaderiv(vertexShader, GL_COMPILE_STATUS, &success);
	if (!success)
	{
		glGetShaderInfoLog(vertexShader, 512, NULL, infoLog);
		std::cout << "ERROR::SHADER::VERTEX::COMPILATION_FAILED\n" << infoLog << std::endl;
	}

	unsigned int fragmentShader = glCreateShader(GL_FRAGMENT_SHADER);
	glShaderSource(fragmentShader, 1, &fragmentShaderSource, NULL);
	glCompileShader(fragmentShader);

	glGetShaderiv(fragmentShader, GL_COMPILE_STATUS, &success);
	if (!success)
	{
		glGetShaderInfoLog(fragmentShader, 512, NULL, infoLog);
		std::cout << "ERROR::SHADER::FRAGMENT::COMPILATION_FAILED\n" << infoLog << std::endl;
	}

	unsigned int shaderProgram = glCreateProgram();
	glAttachShader(shaderProgram, vertexShader);
	glAttachShader(shaderProgram, fragmentShader);
	glLinkProgram(shaderProgram);

	glGetProgramiv(shaderProgram, GL_LINK_STATUS, &success);
	if (!success)
	{
		glGetProgramInfoLog(shaderProgram, 512, NULL, infoLog);
		std::cout << "ERROR::SHADER::PROGRAM::LINKING_FAILED\n" << infoLog << std::endl;
	}

	glDeleteShader(vertexShader);
	glDeleteShader(fragmentShader);

	aPoint a;
	a.x = -0.433f;
	a.y = -0.25f;
	a.z = 0.0f;
	aPoint b;
	b.x = 0.0f;
	b.y = 0.5f;
	b.z = 0.0f;
	aPoint c;
	c.x = 0.433f;
	c.y = -0.25f;
	c.z = 0.0f;
	

	unsigned int VAO, VBO;
	glGenVertexArrays(1, &VAO);
	glGenBuffers(1, &VBO);

	glBindVertexArray(VAO);

	glBindBuffer(GL_ARRAY_BUFFER, VBO);

	glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(float), (void*)0);
	glEnableVertexAttribArray(0);
	glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(float), (void*)(3 * sizeof(float)));
	glEnableVertexAttribArray(1);

	float angle = 0.0f;

	while (!glfwWindowShouldClose(window))
	{
		processInput(window);

		glClearColor(0.2f, 0.3f, 0.3f, 1.0f);
		glClear(GL_COLOR_BUFFER_BIT);

		glm::mat4 trans = glm::mat4(1.0f);
		trans = glm::translate(trans, glm::vec3(Xtranslate, Ytranslate, 0.0));
		trans = glm::rotate(trans, glm::radians(angle), glm::vec3(0.0f, 0.0f, 1.0f));

		angle += direction * (speed);

		glUseProgram(shaderProgram);
		unsigned int transformLoc = glGetUniformLocation(shaderProgram, "transform");
		glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));
		
		dividLine(a, b, depth);
		dividLine(b, c, depth);
		dividLine(c, a, depth);

		glfwSwapBuffers(window);
		glfwPollEvents();
	}

	glDeleteVertexArrays(1, &VAO);
	glDeleteBuffers(1, &VBO);

	glfwTerminate();
	return 0;
}

Thank you for watching it. By the way, Koch snowflakes on the Internet were implemented a few years ago. The interface of OpenGL has been changed.