1. Concept of red black tree
Red Black tree is a binary search tree, but a storage bit is added on each node to represent the color of the node, which can be red or Black. By limiting the coloring mode of each node on any path from root to leaf, the red Black tree ensures that no path will be twice longer than other paths, so it is close to balance.
In practice, red and black trees are generally used for search, which is not a qualitative change compared with AVL trees.
So what's the difference between AVL tree and red black tree?
AVLTREE:
- Binary search tree
- The left and right height of each subtree shall not exceed 1
AVLTREE is strictly balanced.
Red black tree: the longest path is up to twice the shortest path.
The approximate balance of red trees is black.
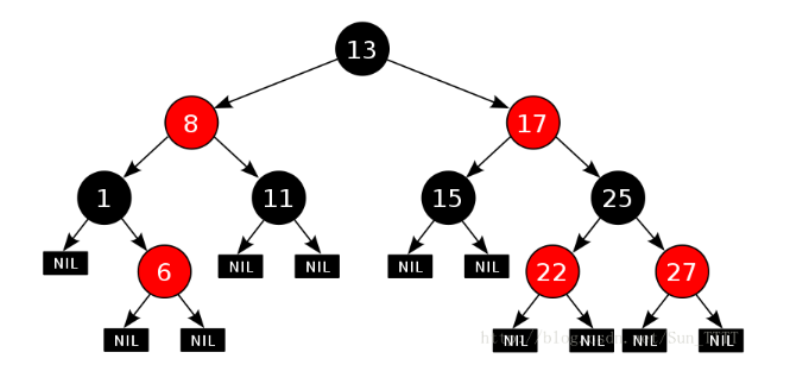
Then why is approximate equilibrium better than strict equilibrium?
Considering the worst case, AVLTREE finds l o g ( N ) log(N) log(N) times, and red black tree search 2 ∗ l o g ( N ) 2*log(N) 2 * log(N) times. In this case, there is no efficiency difference, and AVLTREE constructs more rotations than red and black trees. In general, the efficiency of red black tree is not worse than AVLTREE tree, but the rotation is less than AVLTREE.
2. Properties and principles of red black tree
- Each node is either red or black
- The root node is black
- If a node is red, its two child nodes are black
- For each node, the simple path from this node to all its descendant leaf nodes contains the same number of black nodes
- Each leaf node is black (the leaf node here refers to the empty node)
Why can the red black tree ensure that the number of nodes in its longest path will not exceed twice the number of nodes in its shortest path? (strictly speaking, the main rules are rule 3 and rule 4)
If a node is red, its two child nodes are black - > there are no continuous red nodes in the tree (red and black or continuous black)
For each node, the simple path from the node to all its descendant leaf nodes contains the same number of black nodes - > each path contains the same number of black nodes
Shortest path: all composed of black nodes.
Since the fourth point says that for each node, the simple path from the node to all its descendant leaf nodes contains the same number of black nodes. We can first extract all the black nodes on each path to form a tree. At this time, it must be a full binary tree. At this time, black nodes cannot be added, and only red nodes can be added. If red nodes are not added, the path is the shortest.
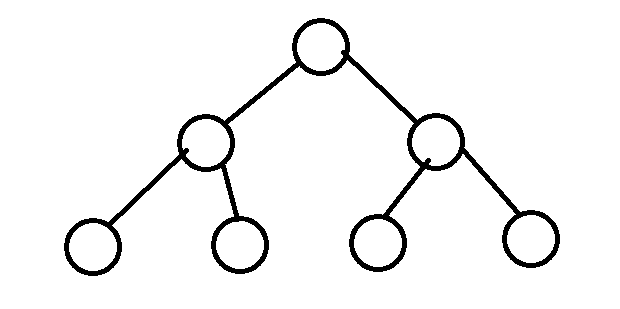
Longest path: add red nodes to the tree composed of all black nodes to construct the longest path.
Since red cannot be continuous, it can only be separated. The longest path constructed is in the state of one black and one red, and the number of black of the longest path is the same as that of the shortest path, so it is up to twice the state.
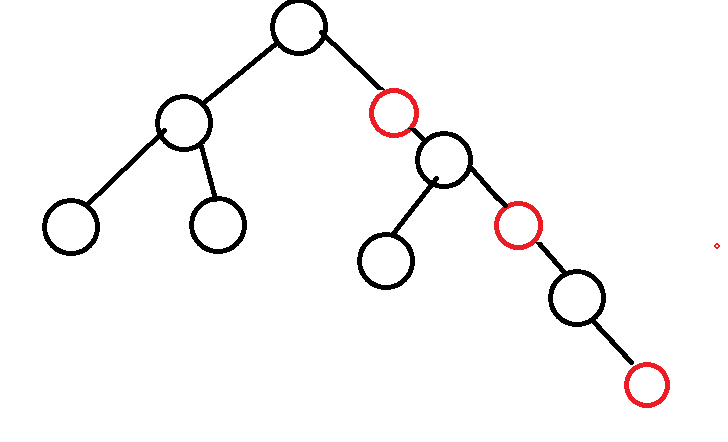
Therefore, assuming that there are N black nodes, the shortest path length is O ( l o g N ) O(logN) O(logN), the longest path length is 2 ∗ O ( l o g N ) 2*O(logN) 2∗O(logN).
So how do you understand the fifth point? It is aimed at meeting the condition of the fourth point in this case.
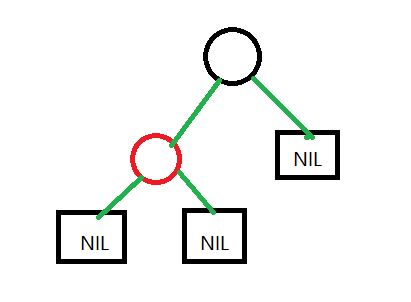
Tips: in a normal red black tree, there may not be the shortest path of all black and the longest path of one black and one red
3. Definition of red black tree node
enum Color
{
RED,
BLACK
};
template<class K, class V>
struct RBTreeNode
{
RBTreeNode(const pair<K,V>& kv)
:_left(nullptr),
_right(nullptr),
_parent(nullptr),
_kv(key_value),
_col(RED)
{}
RBTreeNode<K,V>* _left;
RBTreeNode<K,V>* _right;
RBTreeNode<K,V>* _parent;
pair<K,V> _kv;
Color _col;
};
template<class K,class V>
class RBTree
{
typedef RBTreeNode<K,V> Node;
public:
RBTree()
:_root(nullptr)
{ }
pair<Node*,bool> Insert(const pair<K,V>& kv)
{
}
private:
Node* _root;
}
4. Insertion of red black tree
As long as you control these four rules
- Each node is either red or black
- The root node is black
- If a node is red, its two child nodes are black
- For each node, the simple path from this node to all its descendant leaf nodes contains the same number of black nodes
Can control the approximate balance of red and black trees.
- Is the color of the inserted new node black or red?
Insert red break rule 3 and black break Rule 4.
Insert a red node, because the red node may break rule 3 and has little impact.
Inserting a black node will destroy Rule 4 and affect other paths, with a large influence surface.
For example, inserting a black node into a path will conflict with the rest of the path. Breaking rule three breaks only one fork.
Therefore, when inserting a new node, insert a red node.
Discuss the insertion:
- The parent color is black and does not need to be adjusted. The insertion is completed. (over)
- The parent color is red, which violates rule 3 and needs to be handled. (the key is uncle)
If the parent is red, the grandfather must be black. Look at uncle at this time.
Discuss violations of rule 3:
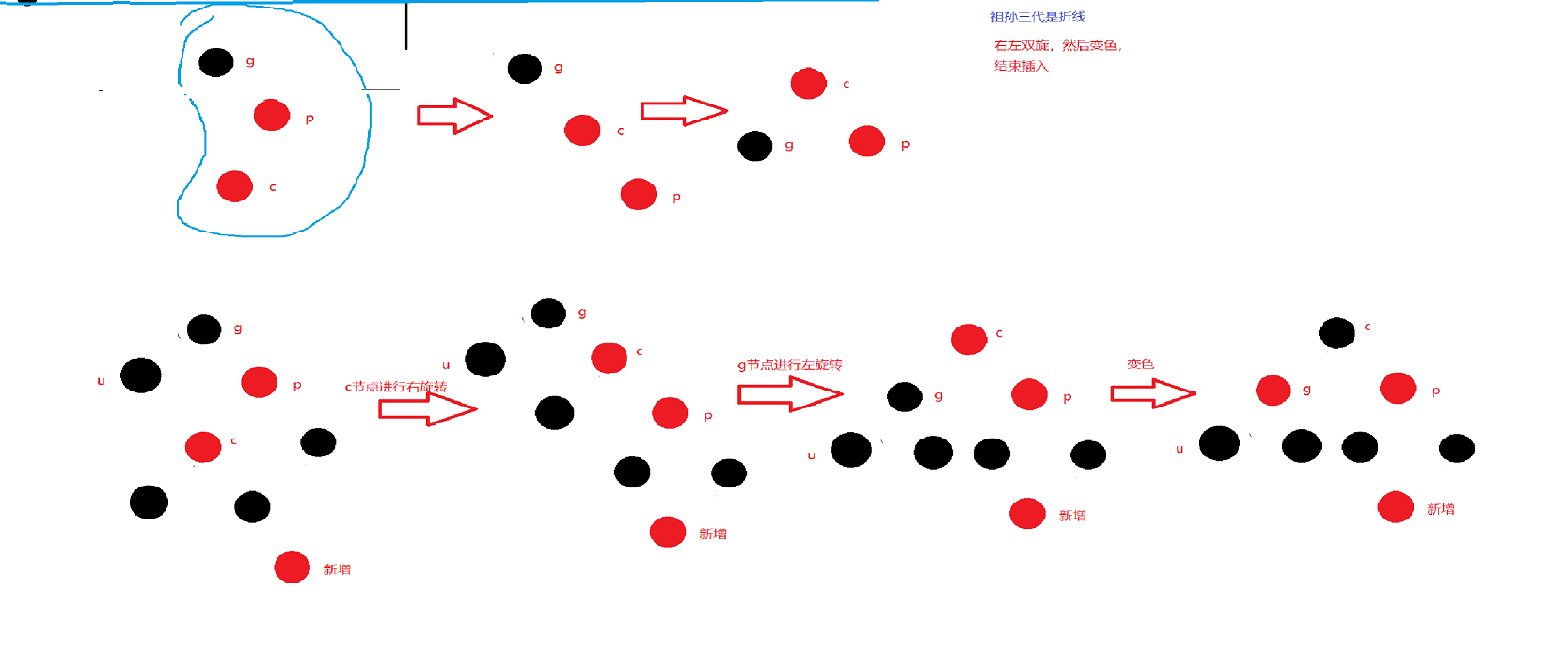
Note: the following figure may be a complete tree or a subtree
4.1 situation I
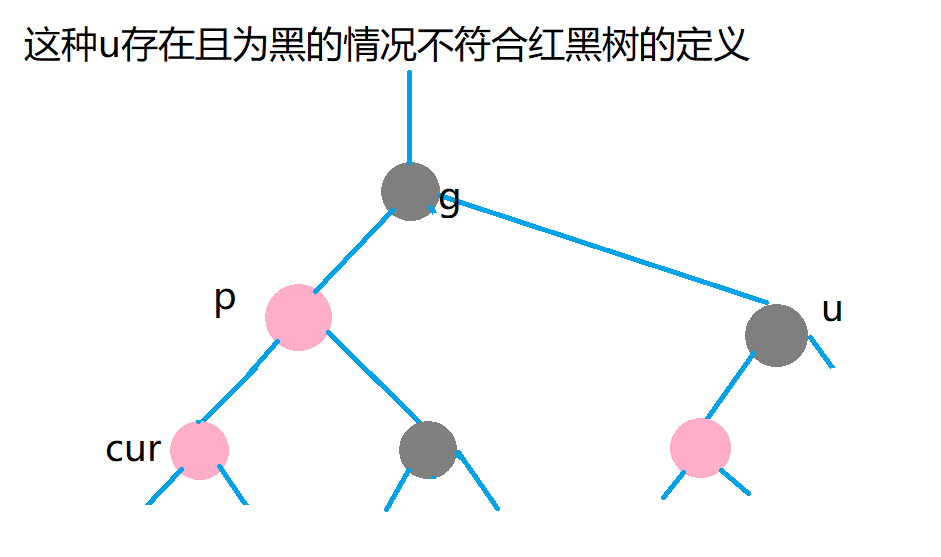
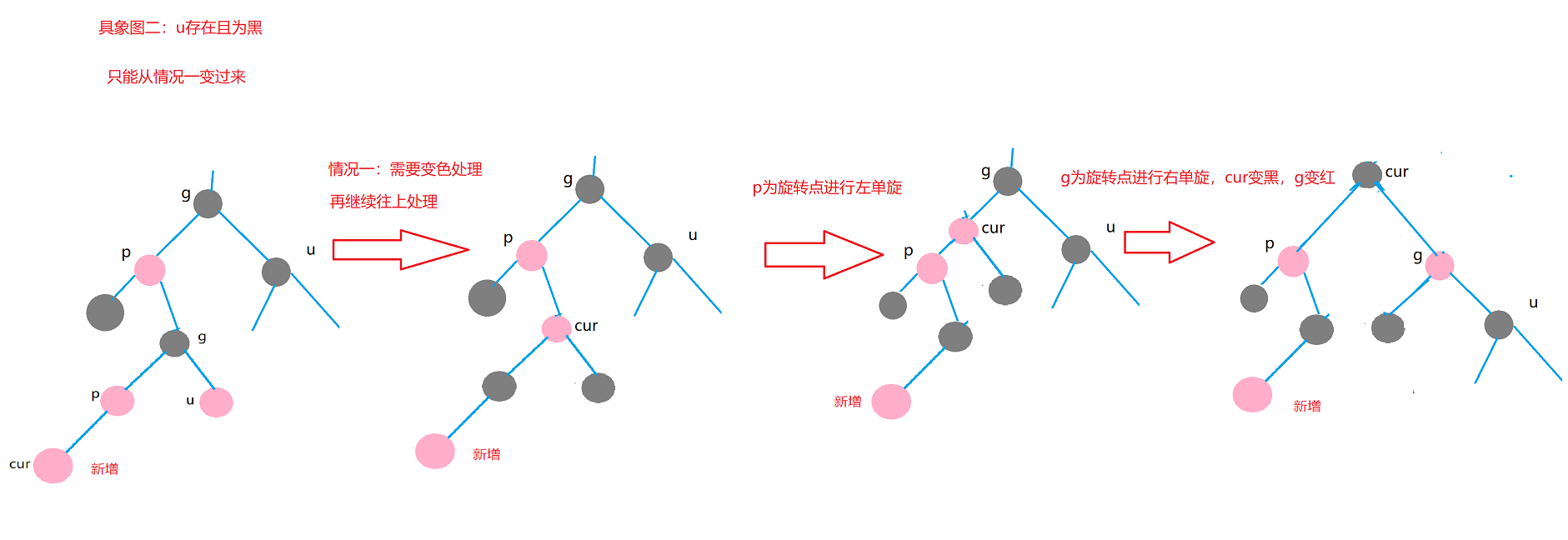
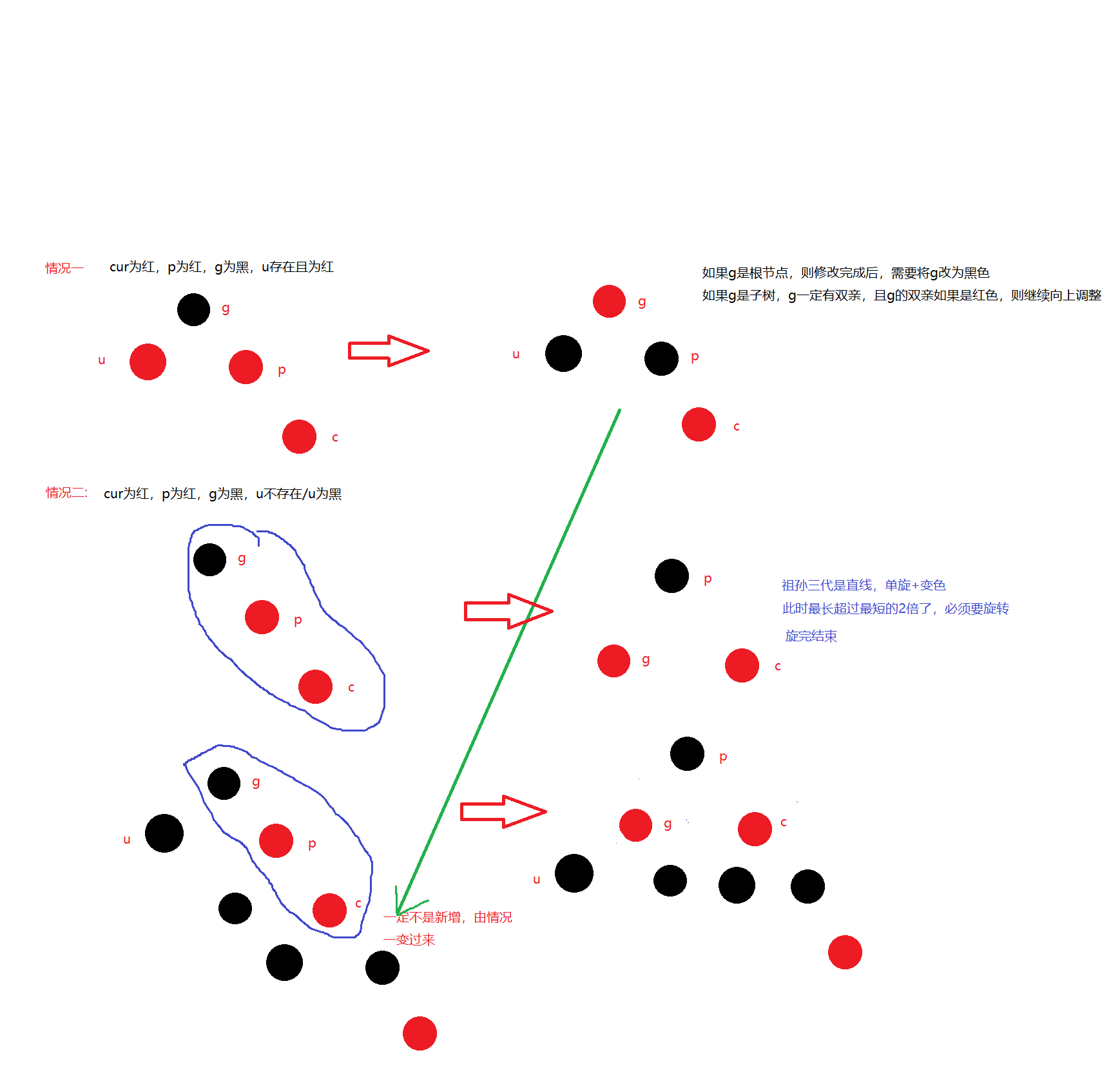
Case 1: cur is red, p is red, g is black, and u exists and is red.
The discussion of a pair of uncles is that uncles exist and are red.
Treatment scheme: p and u turn black and g turns red. After processing, if g is root, it turns black and the processing ends. - > If g's father is red, go ahead
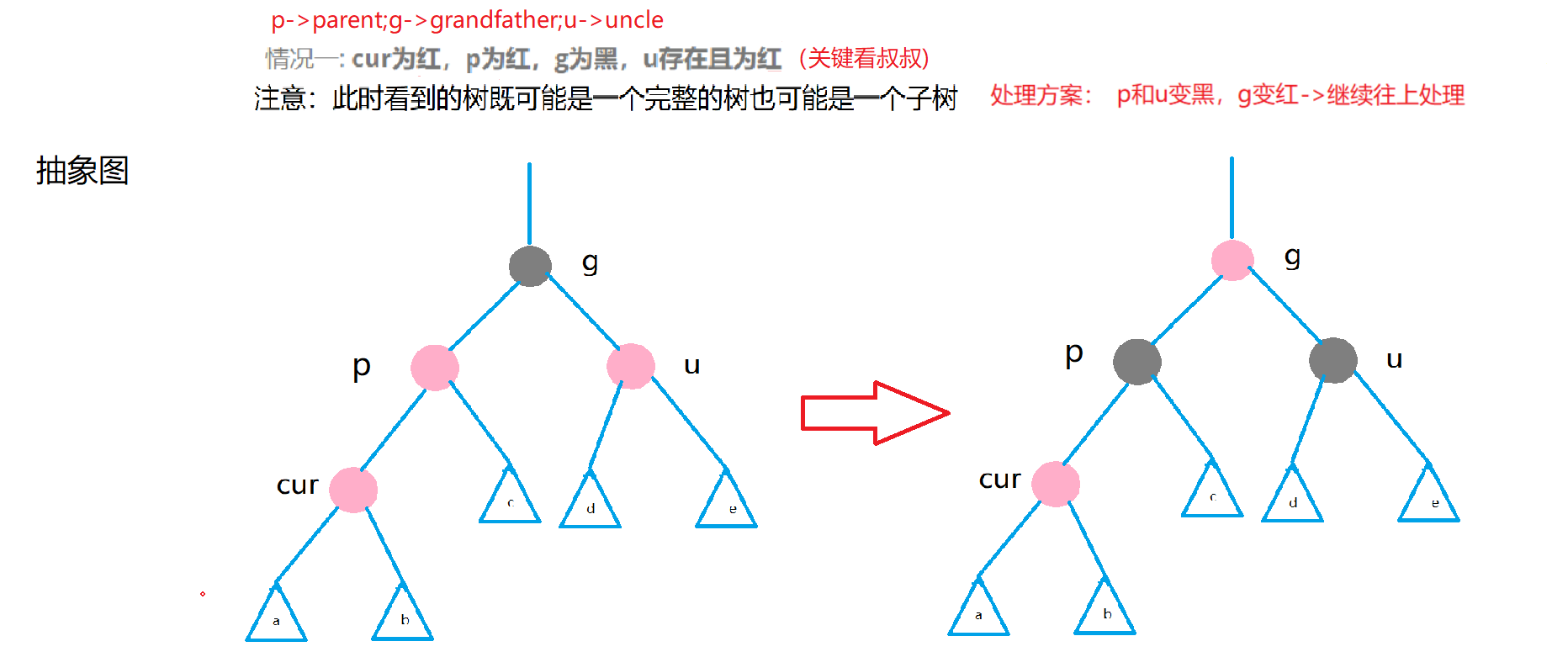
Reason why g turns red: because the current part may be in the subtree. For example, in this case, if G is not red, the two paths of the subtree will have one more black, which conflicts with the path outside the subtree.
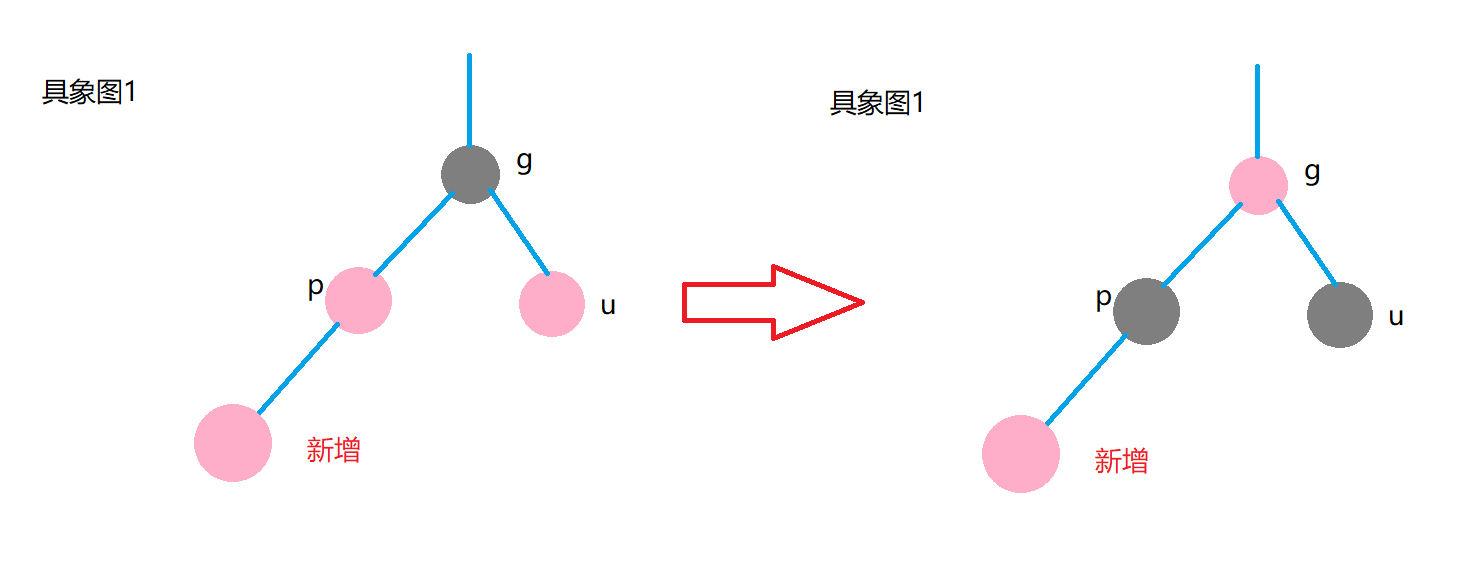
At this time, we should consider that if g's father is black, there will be no problem.
Otherwise, if g's father is red, there will be two red ones at this time. Continue to deal with them.
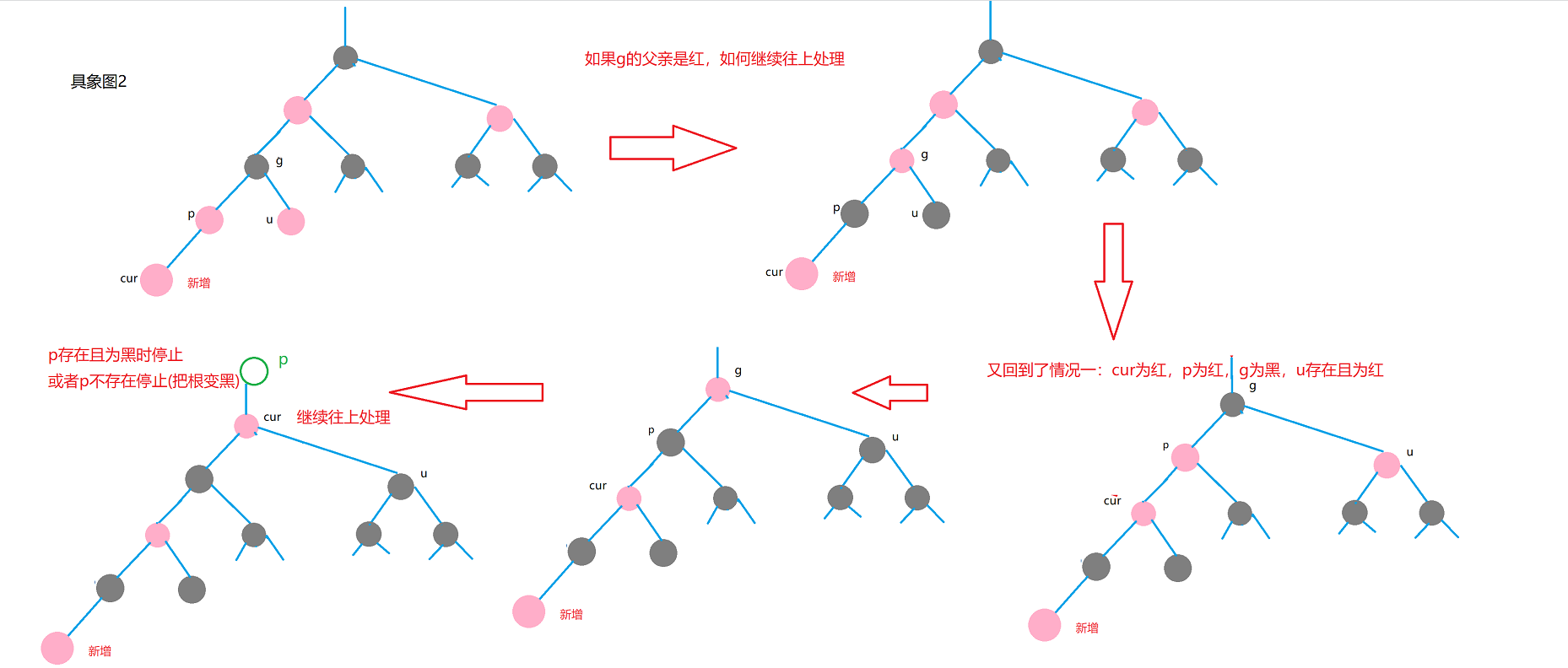
For case 1, the discoloration process can still be completed even if the direction is changed.
4.2 situation II
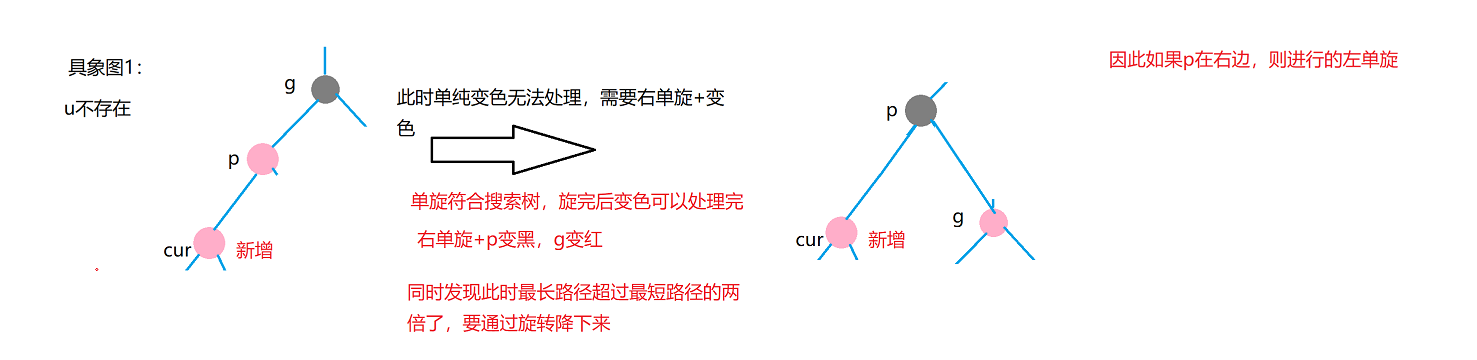
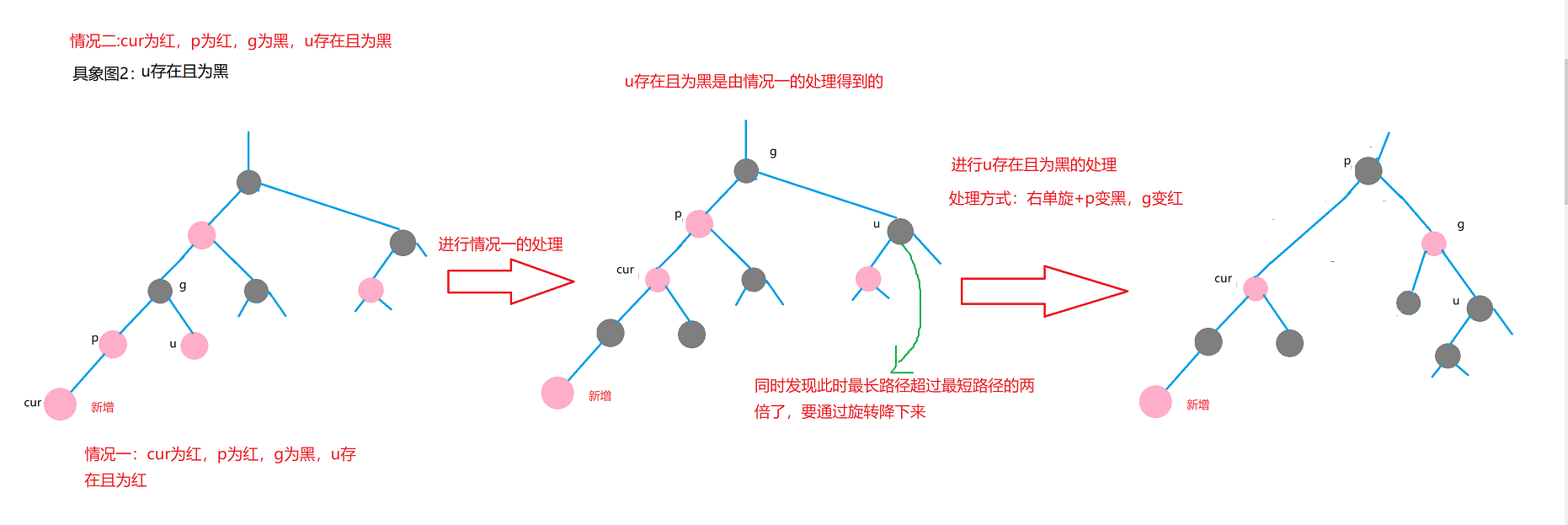
Case 2: cur is red, p is red, g is black, u does not exist / u exists and is black
Treatment method: single rotation + discoloration
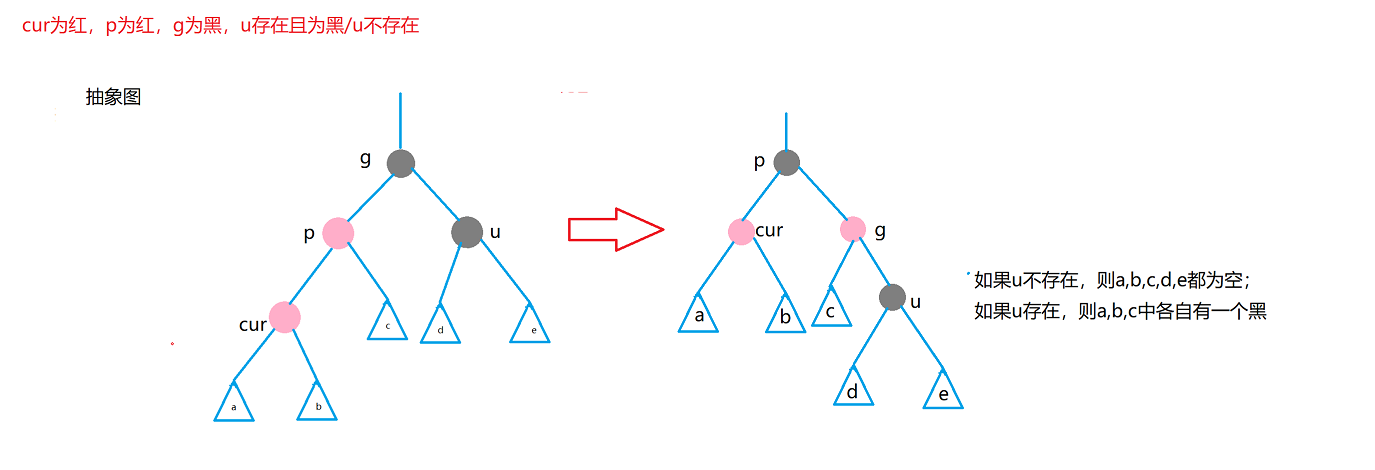
The existence and black of u in case 2 is theoretically obtained from the change after the treatment of case 1.
Therefore, u exists and is black, which needs to be based on the one-time processing of case 1.
- u does not exist
In the red black tree, whenever a rotation is triggered, the longest path must exceed twice the shortest path
- u exists and is black
In case 2, another single rotation + discoloration is carried out in the opposite direction.
4.3 situation III
In the red black tree, whenever a rotation is triggered, the longest path must exceed twice the shortest path
Case 3 is the deformation of case 2. The difference is that case 2 is a straight line and a single rotation; The third case is the curve, which is double rotation.
In case the three directions are reversed, another double rotation + discoloration is carried out.
Case 3: cur is red, p is red, g is black, u does not exist / u exists and is black
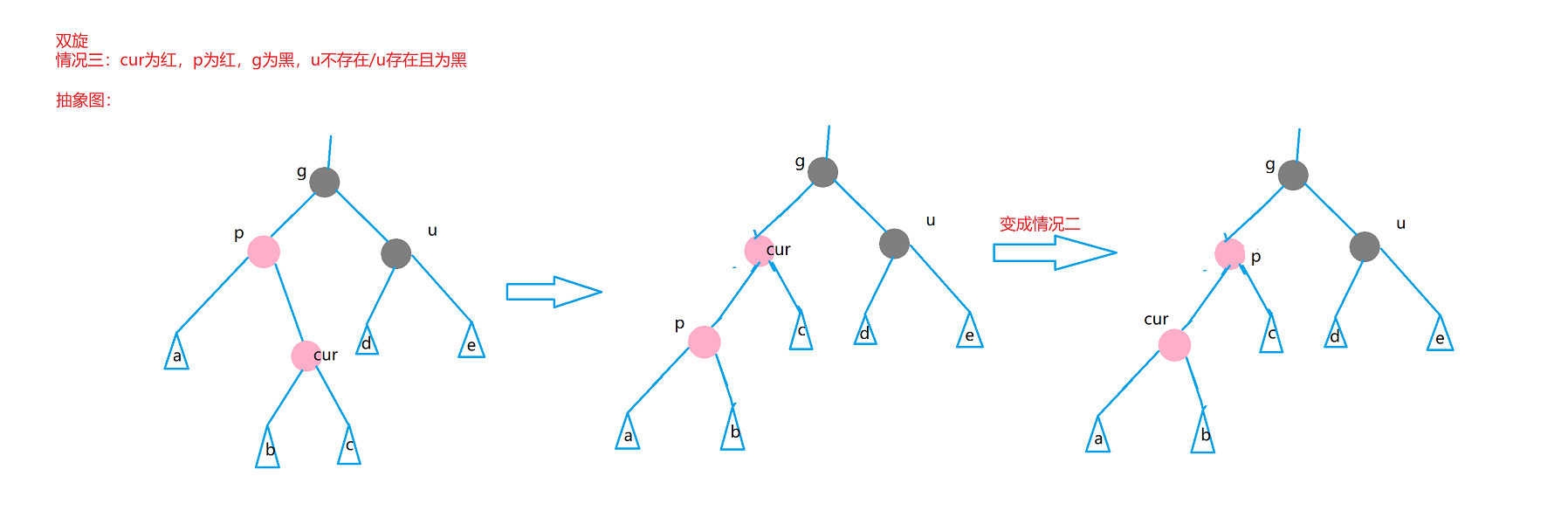
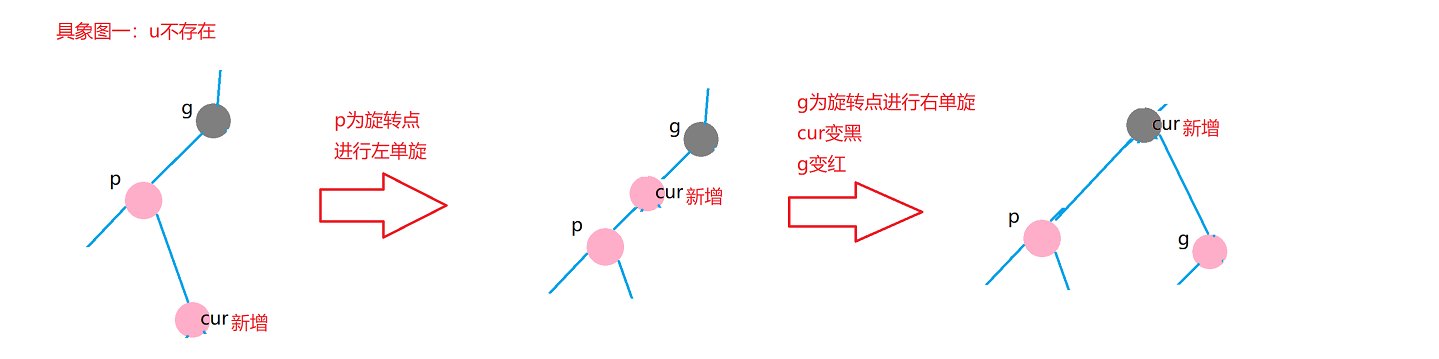
Note that the black nodes at the left end of the following figure p must exist, otherwise the rule of the same number of black nodes in each path cannot be met
4.4 code implementation
For the above three cases, the reverse rotation diagram. See summary
template<class K,class V>
class RBTree
{
typedef RBTreeNode<K,V> Node;
public:
RBTree()
:_root(nullptr)
{ }
void Destroy(Node* root)
{
if(root == nullptr ) return ;
Destroy(root -> _left );
Destroy(root -> _right);
delete root;
}
~RBTree()
{
Destroy(root);
_root = nullptr;
}
//Copy construction and operator [] assignment
Node* Find(const K& key)
{
Node* cur = _root;
while( cur )
{
if( cur -> _kv.first > key)
{
cur = cur -> _left;
}
else if( cur -> _kv.first < key)
{
cur = cur -> _right;
}
else{
return cur;
}
}
return nullptr;
}
void RotateR(Node* parent)
{
Node* subL = parent -> _left;
Node* subLR = subL -> _right;
parent -> _left = subLR;
if( subLR ) subLR -> _parent = parent;
subL -> _right = parent ;
Node* grandParent = parent -> _parent;
parent -> _parent = subL;
if( parent == _root )
{
_root = subL;
_root -> _father = nullptr;
}
else{
if( grandParent -> _left == parent )
{
grandParent -> _left = subL;
}
else{
grandParent -> _right =subL;
}
subL -> _father = grandParent;
}
}
void RotateL(Node* parent)
{
Node* subR = parent -> _right;
Node* subRL = subR -> _left;
parent -> _right = subRL;
if( subRL != nullptr ) {
subRL -> _parent =parent ;
}
subR -> _left = parent;
Node* grandparent = parent -> _parent;
parent -> _parent = subR;
if( parent == _root )
{
_root = subR;
_root -> _parent = nullptr;
}
else{
if(grandparent -> _left == parent)
{
grandparent -> _left = subR;
}
else{
grandparent -> _right = subR;
}
subR -> _parent = grandparent;
}
subR -> _bf = parent -> _bf =0;
}
pair<Node*,bool> Insert(const pair<K,V>& kv)
{
if(_root == nullptr)
{
_root = new Node(kv);
_root = BLACK;
return make_pair(_root,true);
}
Node* parent = nullptr;
Node* cur = _root;
while(cur)
{
if( cur -> _kv.first < kv.first)//If you implement a Mu lt imap, here you use<=
{
parent = cur ;
cur = cur -> _right;
}
else if( cur -> _kv.first > kv.first)
{
parent =cur ;
cur = cur -> _left;
}
else{
return make_pair(cur ,false);
}
}
Node* newnode = new Node(kv);
newnode -> _col = RED;
if( parent -> _kv.first < kv.first)
{
parent -> _right = newnode;
newnode -> _parent = parent;
}
else{
parent -> _left = newnode ;
newnode -> _parent = parent;
}
cur = newnode;
//If the father exists and the color is red, it needs to be handled
while( parent && parent -> _col ==RED)
{
//The key is to see uncle
Node* grandfather = parent -> _parent ; //In the current logical case, grandfather must exist, because the root cannot be red
if(parent == grandfather -> _left)
{
Node* uncle = grandfather -> _right;
//Case 1: uncle exists and is red
if( uncle && uncle -> _col ==RED)
{
parent -> _col = uncle -> _col = BLACK;
grandfather -> _col = RED;
//Continue to process upward
cur = grandfather;
parent = cur -> _parent;
}
else{ //Case 2 + 3 uncle does not exist / uncle exists and is black
if( cur == parent -> _left ) // Case 2: single rotation
{
RotateR(grandfather);
grandfather -> _col = RED;
parent -> _col = BLACK;
}
else{ //Case 3: double rotation
RotateL(parent);
RotateR(grandfather);
cur -> _col = BLACK;
grandfather -> _col = RED;
}
break;//After the rotation, the whole tree becomes a red and black tree
}
}
else// parent == grandfather -> _right;
{
Node* uncle = grandfather -> _left;
if(uncle && uncle -> _col == RED)//Case 1: Uncle exists and is red
{
uncle -> _col = BLACK;
parent -> _col = BLACK;
grandfather -> _col =RED;
cur = grandfather ;
parent = cur -> _father;
}
else{//Case 2 + 3: Uncle exists and is black or does not exist
if( cur == parent -> _right )//Case 2: single rotation + discoloration
{
RotateL(grandfather);
grandfather -> _col =RED;
parent -> _col =BLACK;
}
else{
RotateR(parent);
RotateL(grandfather);
cur -> _col = BLACK;
grandfater -> _col = RED;
}
break;//It must be done after rotation
}
}
}
_root -> _col = BLACK;
return make_pair(newnode ,true);
}
private:
Node* _root;
}
4.5 summary
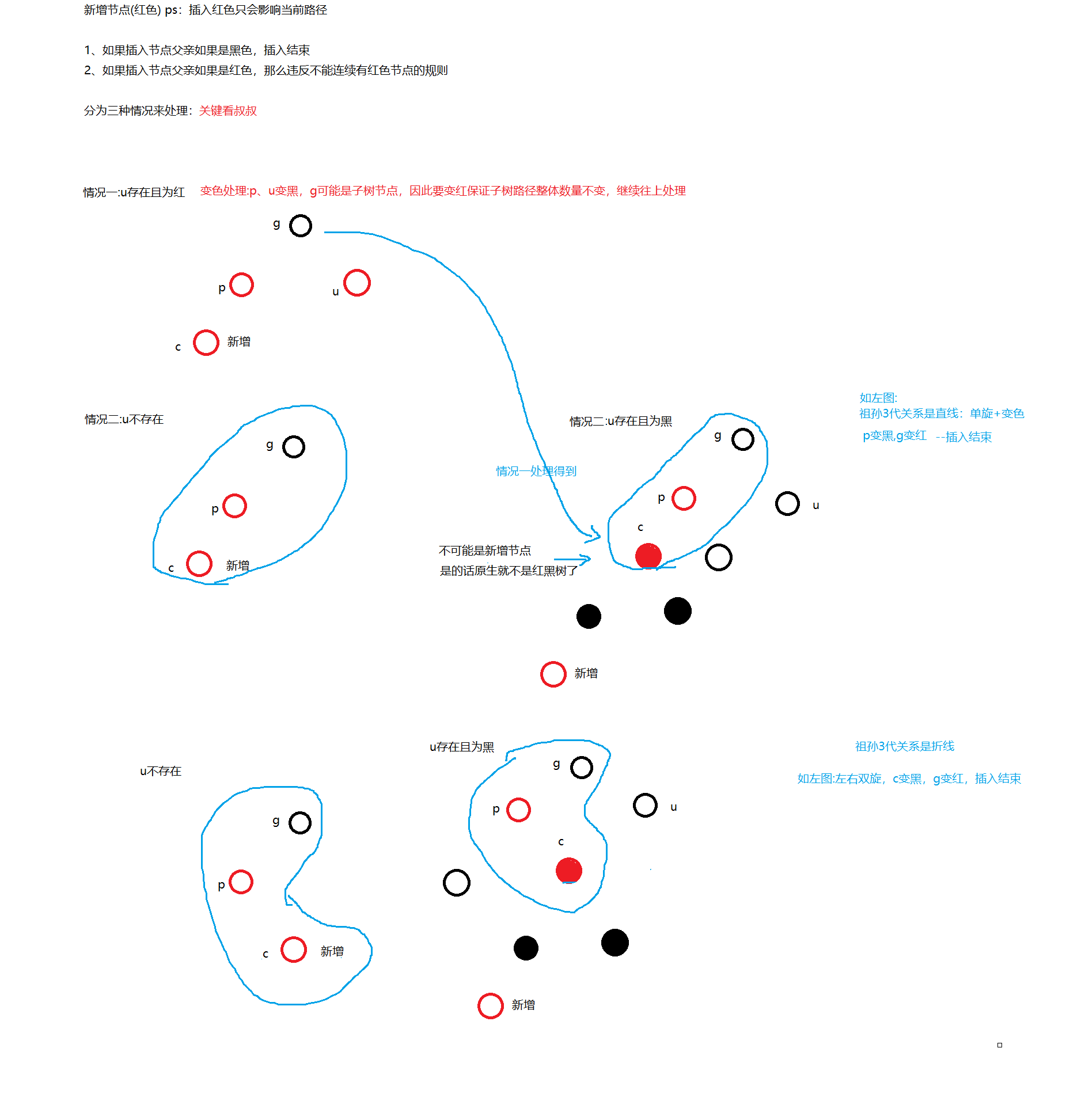
New node (red) ps: inserting red will only affect the current path
1. If the parent of the inserted node is black, the insertion ends
2. If the parent of the inserted node is red, the rule that there can be no consecutive red nodes is violated
First discuss / / /Then discuss the curve, then discuss the case of \, and finally discuss the curve.
Each big situation is divided into three situations through the discussion of the uncle: the key depends on the uncle. If you want to rotate, the current situation must be that the length of the longest path > 2 * the length of the shortest path
5. Inspection of red and black trees
- Each node is either red or black
- The root node is black
- If a node is red, its two child nodes are black -- > the number of black nodes on each path is equal
- For each node, the simple path from this node to all its descendant leaf nodes contains the same number of black nodes
The key point of red black tree balance lies in these rules. We focus on Rules 1, 2 and 3.
The first rule can be checked when entering
For the second point, if you have some trouble checking your son, consider only one son, two sons and no son; It's better to check whether the father and the current node are red when traversing, because the red node theoretically has a father.
For the third point, if you don't open additional space, you can use it O ( N 2 ) O(N^2) O(N2) approach recursion. Or open O ( n ) O(n) O(n) to store the number of black nodes in each path. We try O ( n ) O(n) O(n) time complexity+ O ( 1 ) O(1) O(1) spatial complexity, using a searched standard value.
bool CheckBalance()
{
if( _root == nullptr )
{
return true;
}
if( _root == RED )
{
cout<< " The root node is red " <<endl;
return false;
}
int blackNum =0 ;//Find the leftmost path as the reference value for the number of black nodes
Node* left = _root ;
while(left)
{
if( left -> _col == BLACK)
{
blackNum ++;
}
left = left -> _left;
}
int count = 0;
return _CheckBalance(_root , blackNum,count )
}
bool _CheckBalance(Node* root ,int blackNum ,int count)
{
if( root == nullptr )
{
if( count != blackNum )
{
cout<<" The number of black nodes is not equal "<<endl;
return false;
}
return true;
}
//Inspection rule 2
if(root -> _col == RED && root -> _parent -> _col == RED ) return false;
if(root -> _col == BLACK ) count ++;
return _CheckBalance(root -> _left , blackNum ,count ) && _CheckBalance( root -> _right ,blackNum ,count );
}
#include"RBTree.h"
void TestRBTree()
{
int a[] = { 16 , 3, 7 ,11 ,9 ,26 ,18, 14 ,15};
RBTree<int,int> t;
for(auto e:a)
{
t.insert(make_pair(a,a));
}
t.InOrder();
cout<< t.CheckBlance()<<endl;
}
int main()
{
return 0;
}
6. Deletion of red black tree
Only principle, not implementation. Same as AVL.
- If left is empty and right is empty, delete it directly
- If both sides are not empty, find a replacement node to delete.
The actual deleted node must be empty on the left or empty on the right.
You can understand: http://www.cnblogs.com/fornever/archive/2011/12/02/2270692.html