1, HMM word segmentation idea

HMM implements word segmentation as a sequence annotation task of words in a string.
The basic idea is that each word occupies a certain word formation position (i.e. word position) when constructing a specific word. It is stipulated that each word can only have four word formation positions at most, i.e B B B (initial word) M M M (in words) E E E (suffix) and S S S (separate word).

2, HMM model construction

1. Model state set

Q Q Q = { B B B， M M M， E E E， S S S}， N N N = 4

2. Observation state set

V V V = { I I I, love love Love,...}, a collection of sentences.

3. Observe the status and status sequence

Observation sequence: Xiao Ming is Chinese
Status sequence: B , E , S , B , M , E B, E, S, B, M, E B,E,S,B,M,E

4. State transition probability distribution matrix

In Chinese word segmentation, it is the sequence of states Q Q Q = { B B B， M M M， E E E， S S S} The state probability matrix is obtained in the parameter estimation in the training stage.

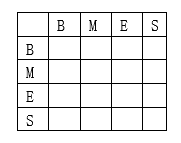
5. Observation state probability matrix (launch probability)

In Chinese word segmentation, the emission probability refers to the state sequence corresponding to each character Q Q Q = { B B B， M M M， E E E， S S S} The probability of each state in the training set is obtained by counting the frequency of the corresponding state of each character in the training set.

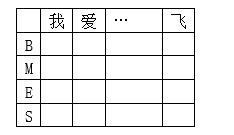
6. Initial probability

In Chinese, the initial state probability of word segmentation refers to the corresponding state probability of the first character of each sentence.
{ B B B: xxx， M M M: xxx， E E E: xxx， S S S: xxx}

7. Objectives

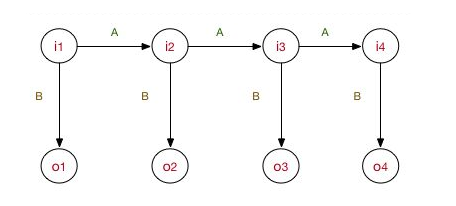
max = m a x P ( i 1 , i 2 , i 3 . . . , i T ∣ o 1 , o 2 , o 3 . . . , o T ) maxP(i_1, i_2, i_3...,i_T | o_1,o_2,o_3... ,o_T) maxP(i1​,i2​,i3​...,iT​∣o1​,o2​,o3​...,oT​)
Of which: T T T is the length of the sentence, o i o_i oi is every word of the sentence, i i i_i ii) is the mark of each word.
According to Bayesian formula:

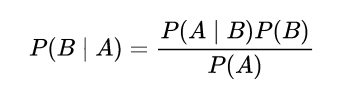
P ( i ∣ o ) P(i | o) P(i∣o) = P ( o ∣ i ) P ( o ) P(o | i) P(o) P(o∣i)P(o) / P ( i ) P(i) P(i)
According to homogeneity HMM:
P ( o ) = p ( o 1 ) p ( o 2 ∣ o 1 ) . . . p ( o t ∣ o t − 1 ) P(o) = p(o1)p(o_2| o_1)...p(o_{t}| o_{t-1}) P(o)=p(o1)p(o2​∣o1​)... p(ot ∣ ot − 1), state transition probability.
P ( o ∣ i ) = p ( o 1 ∣ i 1 ) . . . p ( o t ∣ i t ) P(o | i) = p(o_1| i_1)...p(o_{t}| i_{t}) P(o∣i)=p(o1​∣i1​)... p(ot ∣ it), that is, the probability of generating the observation state (transmission probability).

send P ( o ) P ( o ∣ i ) P(o) P(o | i) P(o)P(o ∣ i) has the highest probability.

3, Corpus

In the people's daily corpus, each line is a sentence, and each word is separated by a space.

IV python code implementation

1. Initialization class

class HMM(object):

    def __init__(self):

        # It is mainly used to access the intermediate results of the algorithm without training the model every time
        self.model_file = './data/hmm_model.pkl'
        # Status value set
        self.state_list = ['B', 'M', 'E', 'S']
        # Parameter loading is used to determine whether the model needs to be reloaded_ file
        self.load_para = False
        # Count the occurrence times of the status, and find p(o)
        self.Count_dic = {}
        # Count the expected total number of rows
        self.line_num = 0

2. Decide whether to retrain

def try_load_model(self, trained):
    """
    It is used to load the calculated intermediate results. When it is necessary to retrain, it is necessary to initialize the emptying results
    :param trained: Training or not
    :return:
    """
    if trained:
        with open(self.model_file, 'rb') as f:
            self.A_dic = pickle.load(f)
            self.B_dic = pickle.load(f)
            self.Pi_dic = pickle.load(f)
            self.load_para = True

    else:
        # State transition probability (State - > conditional probability of state)
        self.A_dic = {}
        # Launch probability (status - > conditional probability of words)
        self.B_dic = {}
        # Initial probability of state
        self.Pi_dic = {}
        self.load_para = False

3. Initialization parameters

def init_parameters(self):
    """
    Initialization parameters
    :return:
    """
    for state in self.state_list:
        self.A_dic[state] = {s: 0.0 for s in self.state_list}
        self.Pi_dic[state] = 0.0
        self.B_dic[state] = {}
        self.Count_dic[state] = 0

4. Mark the input sentences

@staticmethod
def make_label(text):
    """
    Put words according to B,M,E,S tagging
    B: prefix
    M: In words
    E: Suffix
    S: Separate word formation
    :param text:
    :return:
    """
    out_text = []
    if len(text) == 1:
        out_text.append('S')
    else:
        out_text += ['B'] + ['M'] * (len(text) - 2) + ['E']

    return out_text

5. Training

def train(hmm, path):
    # Set of observers, mainly words and punctuation
    words = set()
    line_num = -1
    with open(path, encoding='utf8') as f:
        for line in f:
            line_num += 1

            line = line.strip()
            if not line:
                continue

            # Gets the word for each line and updates the set of words
            word_list = [i for i in line if i != ' ']
            words |= set(word_list)

            # Each line is segmented according to the space and the result of word segmentation
            line_list = line.split()
            line_state = []

            for w in line_list:
                line_state.extend(hmm.make_label(w))
            assert len(word_list) == len(line_state)

            # ['B', 'M', 'M', 'M', 'E', 'S']
            for k, v in enumerate(line_state):
                hmm.Count_dic[v] += 1  # Count the number of occurrences of the status
                if k == 0:
                    hmm.Pi_dic[v] += 1  # The state of the first word of each sentence is used to calculate the initial state probability
                else:
                    # {'B': {'B': 0.0, 'M': 0.0, 'E': 0.0, 'S': 0.0}, ...}
                    # A matrix update: the second state "M", get the previous state "B", B - > M: add one
                    # {'B': {'B': 0.0, 'M': 1.0, 'E': 0.0, 'S': 0.0}, ...}
                    hmm.A_dic[line_state[k - 1]][v] += 1  # Calculate transition probability

                    # {'B': {}, 'M': {}, 'E': {}, 'S': {}}
                    # ['1', '9', '8', '6', 'year', 'year', ']
                    # {'B': {}, 'M': {'９': 1.0}, 'E': {}, 'S': {}}
                    hmm.B_dic[line_state[k]][word_list[k]] = hmm.B_dic[line_state[k]].get(word_list[k], 0) + 1.0  # Calculate launch probability

    hmm.line_num = line_num
    
    # A_dic
    # {'B': {'B': 0.0,      'M': 162066.0, 'E': 1226466.0, 'S': 0.0},
    #  'M': {'B': 0.0,      'M': 62332.0,  'E': 162066.0,  'S': 0.0},
    #  'E': {'B': 651128.0, 'M': 0.0,      'E': 0.0,       'S': 737404.0},
    #  'S': {'B': 563988.0, 'M': 0.0,      'E': 0.0,       'S': 747969.0}
    #  }

    # B_dic
    # {'B': {'medium': 12812.0, 'son': 464.0, 'step': 62.0},
    #  'M ': {' medium ': 12812.0,' son ': 464.0,' step ': 62.0},
    #  'E': {'medium': 12812.0, 'son': 464.0, 'step': 62.0},
    #  'S': {'medium': 12812.0, 'son': 464.0, 'step': 62.0},
    # }

    # Count_dic: {'B': 1388532, 'M': 224398, 'E': 1388532, 'S': 1609916}
    calculate_probability(hmm)


# Calculate probability
def calculate_probability(hmm):

    # Finding probability
    hmm.Pi_dic = {k: v * 1.0 / hmm.line_num for k, v in hmm.Pi_dic.items()}
    # Probability of transition state
    hmm.A_dic = {k: {k1: v1 / hmm.Count_dic[k] for k1, v1 in v.items()} for k, v in hmm.A_dic.items()}
    # 1 plus smoothing
    hmm.B_dic = {k: {k1: (v1 + 1) / hmm.Count_dic[k] for k1, v1 in v.items()} for k, v in hmm.B_dic.items()}

    with open(hmm.model_file, 'wb') as f:
        pickle.dump(hmm.A_dic, f)
        pickle.dump(hmm.B_dic, f)
        pickle.dump(hmm.Pi_dic, f)

6. Viterbi algorithm annotation, word segmentation according to annotation

def viterbi(self, text, states, start_p, trans_p, emit_p):
    V = [{}]
    path = {}
    for y in states:
        V[0][y] = start_p[y] * emit_p[y].get(text[0], 0)
        path[y] = [y]
    for t in range(1, len(text)):
        V.append({})
        newpath = {}

        # Check whether there is this word in the transmission probability matrix of training
        neverSeen = text[t] not in emit_p['S'].keys() and \
                    text[t] not in emit_p['M'].keys() and \
                    text[t] not in emit_p['E'].keys() and \
                    text[t] not in emit_p['B'].keys()
        for y in states:
            emitP = emit_p[y].get(text[t], 0) if not neverSeen else 1.0  # Set unknown words to separate words
            (prob, state) = max(
                [(V[t - 1][y0] * trans_p[y0].get(y, 0) *
                  emitP, y0)
                 for y0 in states if V[t - 1][y0] > 0])
            V[t][y] = prob
            newpath[y] = path[state] + [y]
        path = newpath

    if emit_p['M'].get(text[-1], 0) > emit_p['S'].get(text[-1], 0):
        (prob, state) = max([(V[len(text) - 1][y], y) for y in ('E', 'M')])
    else:
        (prob, state) = max([(V[len(text) - 1][y], y) for y in states])

    return prob, path[state]

def cut(self, text):
    import os
    if not self.load_para:
        self.try_load_model(os.path.exists(self.model_file))
    prob, pos_list = self.viterbi(text, self.state_list, self.Pi_dic, self.A_dic, self.B_dic)
    begin, next = 0, 0
    for i, char in enumerate(text):
        pos = pos_list[i]
        if pos == 'B':
            begin = i
        elif pos == 'E':
            yield text[begin: i + 1]
            next = i + 1
        elif pos == 'S':
            yield char
            next = i + 1
    if next < len(text):
        yield text[next:]

7. Test

if __name__ == '__main__':
    hmm = HMM()
    hmm.try_load_model(True)

    # Initialize state transition matrix
    hmm.init_parameters()

    # print(hmm.A_dic)
    # print(hmm.B_dic)
    # print(hmm.Pi_dic)

    train(hmm, './data/trainCorpus.txt_utf8')

    text = 'This is a great plan!'
    res = hmm.cut(text)
    print(text)
    print(str(list(res)))

8. Results