Sparse array
Introduction:
The following figure is a go board with 11 rows and 11 columns, which is displayed by using a two-dimensional array. At this time, the user needs to save the game. There are two ways to store the game. The first way is to use the two-dimensional array to store it intact on the disk, and the second way is to convert it into a sparse group and store it on the disk. When it is opened next time, the sparse array will be restored to a two-dimensional array.
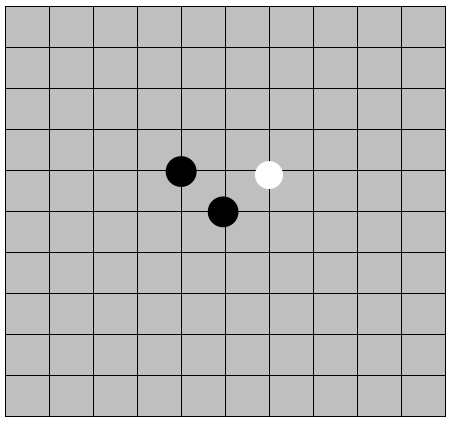
Prototype of sparse array:
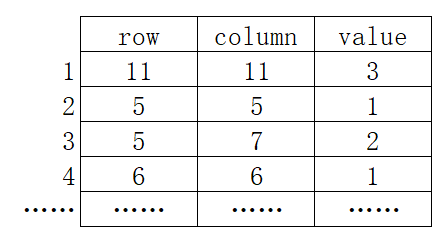
explain:
The first row: the first column represents the number of rows of the original two-dimensional array, the second column represents the number of columns of the original two-dimensional array, and the third column represents the number of elements in the original two-dimensional array that are different from the initial value (in this example, what is the total number of sunspots and whites?)
The second row: the first column represents the row of the first element different from the initial value, the second column represents the column of the first element different from the initial value, and the third column represents the value of the first element different from the initial value.
Line 3: similar to line 2
......
The value + 1 of the third column of the first row of the sparse array is the number of rows of the sparse array. The number of columns of the sparse array is fixed to three columns.
Realization idea:
1, The idea of converting from original two-dimensional array to sparse array:
1 traverse the original two-dimensional array and count the number of elements that are different from the default value num
2 create a sparse array, which is a two-dimensional array of [num+1] rows and [3] columns
3 the three values of the first row of the sparse array are the row, column and [num] of the original two-dimensional array
4 traverse the original two-dimensional array again, and store the elements different from the original value into the second row to [num+1] row of the sparse array in turn. The first column of each row stores the index of the row where the element is located, the second column stores the index of the column where the element is located, and the third column stores the value of the element.
2, The idea of restoring a sparse array to an original two-dimensional array:
1 take out the values of column 1 and column 2 of the first row of the sparse array, which are the number of rows and columns of the original two-dimensional array respectively, and then create a two-dimensional array.
2 traverse the sparse array from the second line and restore it to the whole original two-dimensional array. The first column of each row is the index of the row of the element in the original two-dimensional array, the second column is the index of the column of the element in the original two-dimensional array, and the third column is the value of the element.
Code implementation:
public class ArithmeticChess {
@Test
public void testChess(){
int length = 11;
int[][] arrChess1 = new int[length][length];
System.out.println("=================Original array===============");
arrChess1[5][5] = 1;
arrChess1[5][7] = 2;
arrChess1[6][6] = 1;
int sum = 0;
for (int[] arr : arrChess1) {
for (int i : arr) {
System.out.printf("%3d",i);
if (i != 0){
sum++;
}
}
System.out.println();
}
System.out.println("=================Sparse array===============");
int[][] sparse = new int[sum + 1][3];
sparse[0][0] = length;
sparse[0][1] = length;
sparse[0][2] = sum;
int count = 0;
for (int i = 0; i < arrChess1.length; i++) {
for (int j = 0; j < arrChess1[i].length; j++) {
if (arrChess1[i][j] != 0){
count++;
sparse[count][0] = i;
sparse[count][1] = j;
sparse[count][2] = arrChess1[i][j];
}
}
}
for (int[] arr : sparse) {
for (int i : arr) {
System.out.printf("%3d",i);
}
System.out.println();
}
System.out.println("=================Convert sparse array to original array===============");
int[][] arrChess2 = new int[sparse[0][0]][sparse[0][1]];
for (int i = 1; i < sparse.length; i++) {
arrChess2[sparse[i][0]][sparse[i][1]] = sparse[i][2];
}
for (int[] arr : arrChess2) {
for (int i : arr) {
System.out.printf("%3d",i);
}
System.out.println();
}
}
}
Test output results:
=================Original array=============== 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 2 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 =================Sparse array=============== 11 11 3 5 5 1 5 7 2 6 6 1 =================Convert sparse array to original array=============== 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 2 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Application scenario of sparse array:
1. Chessboard storage
2 Matrix Storage
Source address:
https://gitee.com/wang-hailei/arithmetic/tree/main