1 Problem Description
What is the Dijkstra algorithm?

Dijkstra algorithm function: Give a vertex in weighted connected graph, called the starting point, to find the shortest distance between the starting point and all other vertices.

Dijkstra algorithm idea: using greedy method to search n-1 times (PS:n is the total number of vertices of weighted connected graphs, except the starting point, there are n-1 vertices left), the first time to search, find the nearest vertex from the starting point, marked as traversed; the next time to search, never been traversed vertex search. Find a vertex closest to the starting point, marked as traversed; until n-1 search is completed, the search is completed, and the final result is returned.

2 Solutions
2.1 Use Dijkstra algorithm to get the shortest distance example
Here, I borrow an illustration from the Blog at the end of Reference 1 (PS: Personally, this illustration is easy to understand):

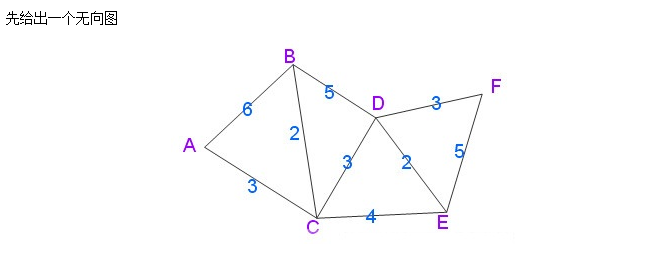
2.2 Specific Coding
Dijkstra complexity is O(N^2). If the binary heap optimization can achieve O((E+N)logN), the fibonacci heap can be optimized to O(NlogN+E).

Note that the Dijkstra algorithm can only be applied to graphs without negative weights. Because this condition is satisfied in most applications, this limitation does not affect the wide application of Dijkstra algorithm.

Secondly, we should pay attention to distinguishing the Dijkstra algorithm from the Prim algorithm for finding the smallest spanning tree. Both of them are based on greedy idea, but Dijkstra algorithm is to compare the length of the path, so we must add the weights of the edges between the starting point and the corresponding vertex, while Prim algorithm is to directly compare the weights given by the corresponding edges.

The time complexity of the following code is O(N^2), and the figure used in the code is 2.1. The figure given in the shortest distance example is obtained by using the Dijkstra algorithm.

package com.liuzhen.chapter9;

public class Dijkstra {
    /*
     * Parametric adjMatrix: The weight matrix of a graph. Two vertex representations with a weight of -1 cannot be directly connected.
     * Function: Return the shortest distance from vertex 0 to all other vertices, where the shortest distance from vertex 0 to vertex 0 is 0
     */
    public int[] getShortestPaths(int[][] adjMatrix) {
        int[] result = new int[adjMatrix.length];   //The shortest distance used to store vertex 0 to other vertices
        boolean[] used = new boolean[adjMatrix.length];  //Used to determine whether a vertex is traversed
        used[0] = true;  //Represents that vertex 0 has been traversed
        for(int i = 1;i < adjMatrix.length;i++) {
            result[i] = adjMatrix[0][i];
            used[i] = false;
        }
    
        for(int i = 1;i < adjMatrix.length;i++) {
            int min = Integer.MAX_VALUE;    //The shortest distance between vertex 0 and i for temporary storage is initialized to Integer-type maximum
            int k = 0;
            for(int j = 1;j < adjMatrix.length;j++) {  //Find a vertex with the smallest distance from vertex 0 to other vertices
                if(!used[j] && result[j] != -1 && min > result[j]) {
                    min = result[j];
                    k = j;
                }
            }
            used[k] = true;    //The vertex with the smallest distance is recorded as traversed
            for(int j = 1;j < adjMatrix.length;j++) {  //Then, the distance between vertex 0 and other vertices is compared with the distance after adding intermediate vertex k, and the shortest distance is updated.
                if(!used[j]) {  //When vertex j is not traversed
                    //Firstly, vertex k to vertex J must be able to pass through; then, when the distance from vertex 0 to vertex J is greater than the distance from vertex 0 to k to j or vertex 0 cannot reach vertex J directly, the shortest distance from vertex 0 to vertex J is updated.
                    if(adjMatrix[k][j] != -1 && (result[j] > min + adjMatrix[k][j] || result[j] == -1))
                        result[j] = min + adjMatrix[k][j];
                }
            }
        }
        return result;
    }
    
    public static void main(String[] args) {
        Dijkstra test = new Dijkstra();
        int[][] adjMatrix = {{0,6,3,-1,-1,-1},
                {6,0,2,5,-1,-1},
                {3,2,0,3,4,-1},
                {-1,5,3,0,2,3},
                {-1,-1,4,2,0,5},
                {-1,-1,-1,3,5,0}};
        int[] result = test.getShortestPaths(adjMatrix);
        System.out.println("The shortest distance between vertex 0 and all vertices in the graph is:");
        for(int i = 0;i < result.length;i++) 
            System.out.print(result[i]+" ");
    }
}

Operation results:

The shortest distance between vertex 0 and all vertices in the graph is:
0 5 3 6 7 9