**

Implementing two sorting BFS/DFS algorithms with Python class

What are BFS and DFS algorithms
Code implementation of BFS and DFS algorithms
BFS and DFS algorithm (Lecture 3) -- from BFS to Dijkstra algorithm

Idea:
When you do this problem, you should first create a lot of nodes, and then build the connection relationship between nodes, and break up the sorting. If you think about the characteristics of the root node, you can easily find the root node.
In addition, the creation of nodes can have their own creation methods, and the attributes can have input node and output node, and then directly build the network according to the input and output. This left and right node method is still easy
Provide code templates for thinking:

# coding:utf8

class Node:
    
    def __init__(self,name,value):
        self.name = name
        self.value = value
        self.input_node = [] # name of input node
        self.output_node = [] # name of output node
        self.depth = 0 # Used to set depth in dfs sorting
        self.index = -1 # Store the index of the node after taking the order. If not, the ready is - 1
        
    def setInput(self,name):
        self.input_node.append(name)
    
    def setOutput(self, name):
        self.output_node.append(name)
        
    def __repr__(self):
        return self.name
        

        
class Net:
    ''' Deep learning net There are differences node Connected, each node All have input node and output node
    When each node input It can only be calculated after we have calculated. Our ultimate goal is to follow the order in which we shoot
    To execute, the results can be calculated smoothly'''
    
    def __init__(self,node):
        self.input = [] #net input node
        self.output = [] # net output node
        self.node = [] # Put it here in disorder
        self.ordered_node = [] #Put it here in order
        
    def addnode(self,node):
        self.node.append(node)
        
    def __getitem__(self,index): # Get the node of the ordered index
        return self.ordered_node[index]
        
    def dfs(self):
        """ Realize in-depth prioritization by yourself. Ideas:
        1,Find already ready Node: input_node Empty or input node All already ready
        2,take ready of node Deposit self.ordered_node,
        3,Establish temporary list deposit unredy_node
        4,establish stack_list Store to be processed node，from self.ordered_node Medium selection node find output The node is stacked and ready for processing
        5,Nodes in the processing stack:
                A,If the node is already ready If necessary: handle it by yourself(Key point: the node can be released only after all child nodes of the node are processed)；
                B,without ready，Put the node on the stack;
        """
        
        pass
        return self.ordered_node
    
    def bsf(self):
        """ Implementation of breadth priority, set each node And then sort by depth"""
        pass
        
        return self.ordered_node
        
    
    
if __name__ == "__main__":
    
    node = [node1, node2, node3, node4, node5] # Establish your own node and specify the connection relationship
    net = Net(node)
    resulf1 = net.dfs()
    result2 = net.bsf()

Template method
Topics using BFS and DFS are generally marked as medium or hard on leetcode. However, from the perspective of thinking logic, the definition of difficulty is too high. From the perspective of code volume, it may take more time to write a BFS or DFS than other types of topics.
Since BFS and DFS have fixed thinking, they must have their own routines. Apply the template method to make our problem-solving more smooth. It's like a cook solving an ox with ease.

BFS template
The idea of BFS is to add neighbors first. If it's just oral, it's inevitably boring.
The following will take the search on the figure (finding the shortest distance between start_node and end_node) as an example to illustrate how to turn thinking into code.

Get graph
Just as a linked list is essentially a node and a pointer to the next node, the essence of a graph is the node on the graph and the edge connecting each node.
Therefore, there are actually two ways to represent a graph (there is no distinction between a directed graph and an undirected graph):

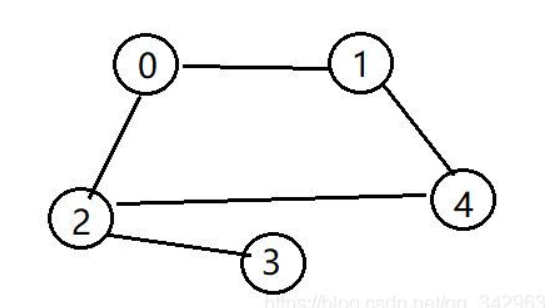
The graph is represented by edges between nodes.
If I draw a sketch, the graph can be represented by edges[[0,1],[0,2],[1,4],[2,3],[2,4]], and each edge connects two vertices. According to the title, you can specify whether it is the edge of a directed graph.
The diagram is represented by node to node connections
Suppose the graph has n nodes and there are 5 nodes in the sketch. Then the graph is expressed as [[1,2], [0,4], [0,3], [2], [1,2]]. The index in the graph represents the label of the node, that is, node 0 is connected with nodes 1 and 2, and so on. This correspondence can also be represented by a dictionary.
The first step of BFS is to get the map. You can use either of these two methods, depending on your familiarity and the speed of problem solving.
Of course, you can build a graph based on edges, which is not very difficult:
The graph is represented by edges between nodes.
If I draw a sketch, the graph can be represented by edges[[0,1],[0,2],[1,4],[2,3],[2,4]], and each edge connects two vertices. According to the title, you can specify whether it is the edge of a directed graph.
The diagram is represented by node to node connections
Suppose the graph has n nodes and there are 5 nodes in the sketch. Then the graph is expressed as [[1,2], [0,4], [0,3], [2], [1,2]]. The index in the graph represents the label of the node, that is, node 0 is connected with nodes 1 and 2, and so on. This correspondence can also be represented by a dictionary.
The first step of BFS is to get the map. You can use either of these two methods, depending on your familiarity and the speed of problem solving.
Of course, you can build a graph based on edges, which is not very difficult:

def initial_graph(n, edges):
    dict_graph = {}

    for i in range(n):
        dict_graph[i] = []
        
    num_e = len(edges)
    for i in range(num_e):
        u = edges[i][0]
        v = edges[i][1]
        dict_graph[u].append(v)
        dict_graph[v].append(u)

    return dict_graph

Use queue
It is suitable for first in, first out, bfs.
Two methods of importing python queue are:

1. Use queue

from queue import Queue
q = Queue() # I don't quite understand the definition and why it involves the design of python
q.put(node) # Put
q.get() # Out of the team

2. Use deque

import collections
q = collections.deque() # Bidirectional queue
q.append() # Join the team
q.popleft() # Out of the team 

Node queue

Define using Queue()

q.put(start_node)

To prevent backtracking in an undirected graph, set blocking is used

hash_set = set()
hash_set.add(start_node)

bfs main body, the part that needs to be recited

step = 0
while not q.empty():
	size = len(q)
	step += 1
	for iter_num in range(size):
		node = q.get() # current node
		# get the neighbor
		for neighbor in dict_graph[node]: 
			if neighbor == end_node: # find it!!!!
				return step
			if neighbor in hash_set: 
				continue # avoid backtracking
			hast_set.add(node)
			q.put(neighbor)
	return 0 # can't find

Section
The general bfs process is shown above. Some problems and difficulties lie in the detailed implementation of bfs, such as:

• Termination condition of bfs the termination condition of some topics may not be to find an end point, but to clear some elements in the diagram. For example, the problem of zombies eating people needs to turn all people into zombies.
  The queued element indicates that a tuple (node,
  step) join the team and unpack when leaving the team, so as to write one less layer of cycle and speed up to a certain extent. For example, the wordList given by case is actually very long.

DFS template

• DFS idea is to go to the end, hit the wall and then turn back. Like the above BFS analysis, the following will take finding all subsets of array num as an example to illustrate the process of DFS.

Subset of array

• As like as two peas, the array num[1,2,3] is known (assuming that the array is already sorted). All subsets of dfs are required. The process of the dfs is shown in Figure 2.

  Start from the empty set, and then add 1. After adding 1, add 2 next time, and then add 3. At this time, the startindex pointer moves out of the array range and starts backtracking. After removing 3, trace back to 2 (where the internal loop has ended and executed to the bottom of the function). After tracing back to 2, add 3 to 1 and 1. This is the process of the program. The key is how to write the code.

dfs function definition

• Because dfs involves the recursive call of the program, generally dfs is not embedded into the internal process of the program. In the main function, dfs is called as an auxiliary function, so the dfs function is named dfsHelper.

#In python, the general definitions are as follows:
def dfsHelper(self，
				input parameter..., 
				startIndex, 
				tmp, 
				result):
"""

Of which:
input parameter generally refers to the invariant known quantity: for example, array num, matrix grid in matrix search, graph and target node end in graph_ node；
startIndex is used to mark the position of the current pointer in the array (matrix or graph), which changes with recursion;
tmp: used to temporarily store the structure in the recursive process, which changes with the recursion;
result: generally a global variable, which is used to save all results.
In program writing, you can define many frequently used quantities as constants, so as to make the dfsHelper function shorter and more concise.

dfs recursive process, need to recite

• The recursive process is to first add the current element in tmp, then call itself (the intermediate pointer moves backward), and finally remove the current element in tmp.
  If you don't look at the circular call of dfsHelper, you can understand it this way; When tmp = [], move startIndex backward to add 1, 2 and 3 to tmp in turn, that is, the first layer of search. Dropping the "1"pop keeps the purity of the current layer. Without this operation, the recursive hierarchy will be confused.

for i in range(startIndex, len(nums)):
    tmp.append(nums[i])
    self.dfsHelper(nums, i + 1, tmp, result)
    tmp.pop()

Temporary storage of results

• Because it is to find all subsets, tmp actually saves different subsets each time it recurses. Therefore, tmp should be added to the result at the beginning of dfs function. Because tmp is actually a pointer to an address, which may change at any time in recursion, copy the content of tmp before adding it instead of taking it out directly to ensure the correctness of the running results.
  Can c + + take values directly here? Study it again when you have time.

tmp_copy = tmp.copy()
result.append(tmp_copy)

Outlet of dfs

• The export of dfs is the difficulty of this kind of problem because of its variety. When using startIndex in defining the dfsHelper function, it is obvious that you need to use this flag for judgment. So there are:

if startIndex == len(nums):
    return

In other problems, such as two-dimensional matrix, the index may be out of bounds, or the visited may be defined and accessed at the current location. These specific problems need special treatment.

A panoramic view
The complete solution of this problem is listed below to further understand this problem.

class Solution:
    """
    @param nums: A set of numbers
    @return: A list of lists
    """
    def subsets(self, nums):
        # Start the search from the empty set and add the nodes of num to the empty set each time
        result = []
        tmp = []
        
        if nums is None:
            return None
        
        nums.sort()
        
        startIndex = 0    
        self.dfsHelper(nums, startIndex, tmp, result)
        
        return result
        
    def dfsHelper(self, nums, startIndex, tmp, result):
        # dfs outlet
        tmp_copy = tmp.copy() # Make a copy
        result.append(tmp_copy)
        
        if startIndex == len(nums):
            return
        
        for i in range(startIndex, len(nums)):
            tmp.append(nums[i])
            self.dfsHelper(nums, i + 1, tmp, result)
            tmp.pop()
        return

Summary

• Personally, DFS is more difficult than BFS, because it has a variety of definitions of dfsHelper functions, which can be flexibly defined according to their own needs and habits. However, after changing the vest, the internal thinking has not changed, and the amount of calculation (said complexity) has not changed.
  The so-called algorithm focuses more on "method" than "calculation", that is, it is more a method than an arithmetic.