title: [improve] use the sieve method to find the prime number in N
date:
author: galileocat
img: https://cdn.jsdelivr.net/gh/QiYi92/ImageHost/img/202108051426453.png
top: false
cover: false
coverImg:
password:
toc: false
mathjax: false
summary: Blue Bridge Cup improved
categories: Blue Bridge Cup
tags:
- Blue Bridge Cup
- Python
Title 1084: find the prime number in N by sieve method.
Time limit: 1Sec memory limit: 64MB commit: 14733 resolve: 8802
Title Description
Use the sieve method to find the prime number in N.
input
N
output
Prime numbers from 0 to N
sample input
100
sample output
2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97
Basic judgment method
The nature of prime number: there are only two factors: 1 and itself
# Basic judgment method
def is_prime(n):
for i in range(2,n):
if n%i==0:
return False
return n != 1
n=int(input())
print(is_prime(n))
optimization algorithm
When n is an even number, there is no need to cycle at all. Even numbers other than 2 must be composite numbers.
The first optimization scheme is derived
#optimization algorithm
import math
def is_prime(n):
#When n is even, there is no need to cycle, because even numbers other than 2 must be composite
if n % 2 == 0 and n != 2:
return False
# math,sqrt() returns the square root of the number in parentheses
#Just loop to the square root
for i in range(3,int(math.sqrt(n)+1)):
if n % i == 0:
return False
return n != 1
n=int(input())
print(is_prime(n))
Further optimization algorithm
Continue to optimize. There is a theorem in mathematics that only natural numbers in the form of 6n-1 and 6n+1 may be prime numbers, where n is an integer greater than or equal to 1.
Because all natural numbers can be written as 6n,6n+1,6n+2,6n+3,6n+4,6n+5, of which 6n,6n+2,6n+4 are even numbers and must not be prime numbers. 6n+3 can be written as 3(2n+1), which is obviously not a prime number, so only 6n+1 and 6n+5 can be prime numbers. 6n+5 is equivalent to 6n-1, so we usually write 6n-1 and 6n+1.
#Further optimization algorithm
def is_prime(n):
if n % 6 not in (1,5) and n not in (2,3):
return False
for i in range(3,int(math.sqrt(n)+1)):
if n % i == 0:
return False
return n != 1
Angstrom sieve method
The idea is to use the screened prime numbers to filter all the numbers that can be divided by it. These prime numbers are like a sieve to filter natural numbers. The remaining numbers screened are naturally numbers that cannot be divided by the previous prime numbers. According to the definition of prime numbers, these remaining numbers are also prime numbers.
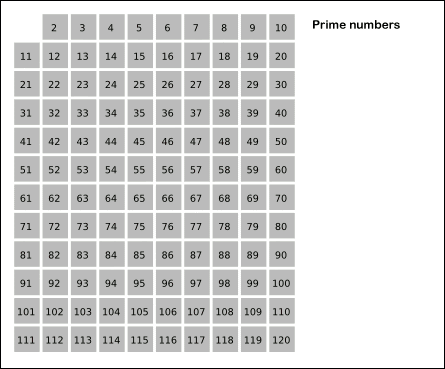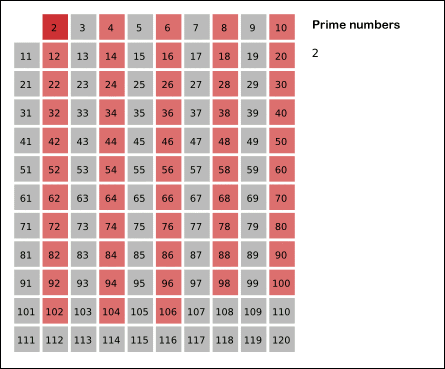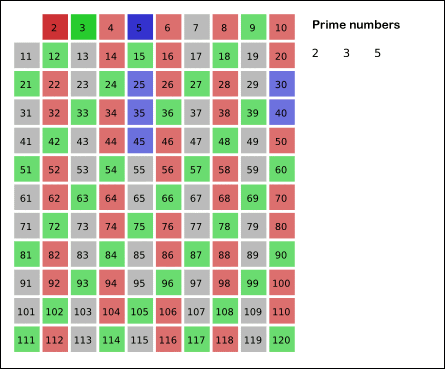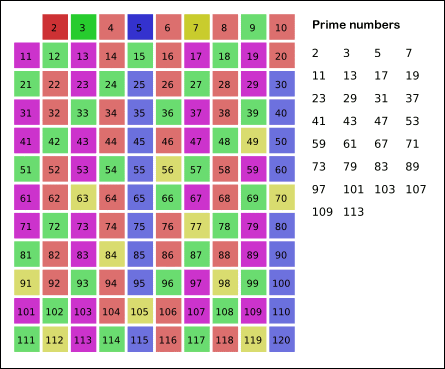
If we want to screen out all prime numbers within 100, we know that 2 is the smallest prime number. We can use 2 to screen out all even numbers first. Then traverse back to 3. 3 is the first number left by 2, which is also a prime number. Then use 3 to screen all the numbers that can be divided by 3. After screening, we continue to traverse. The first number we encounter is 7, so 7 is also a prime number. We repeat the above process until the end of the traversal. At the end, we get all primes within 100.
Use the following dynamic diagram to assist understanding
Algorithm idea:
Create two arrays, one for finding prime and the other for judging is_prime.
The list used to judge prime numbers is_prime=[True]*(n+1) generate
What it looks like after generation [true, true, true, true...]
Then start the 1 cycle from 2 to n+1 and substitute i into is_prime list
If the current i is True, the number is prime
Put it in the prime array and enter the 2 loop
If the current i is False, go directly to cycle 2
2 take the multiple of i (not counting i) in turn in the loop and turn it into False
In this way, every time 1 loops to a multiple of i, append() will not be executed
#Extreme! Angstrom sieve method
def eratosthenes(n): #Eratoshni
primes=[]
is_prime=[True]*(n+1) #Create a list with n+1 trues
for i in range(2,n+1):
if is_prime[i]: #Substitute i into is_ In the prime list, if true, it will be executed; if false, it will not be executed
primes.append(i)
#Use the current prime i to sift out all numbers that can be divided by it
for j in range(i*2,n+1,i): #Take the multiple of i in sequence; Cycle from i*2 to n+1 in steps of i;
is_prime[j]=False
return primes
n=int(input())
print(eratosthenes(n))
Blue Bridge Cup 1084 questions
Application to angstrom sieve method
#Blue Bridge Cup 1084 questions
n=int(input())
primes=[] #Prime sequence
alist=[True]*(n+1) #Overall list
for i in range(2,n+1):
if alist[i]: #Substitute i into the overall list for judgment. If true, continue, and if false, skip
primes.append(i)
for j in range(i*2,n+1,i):
alist[j]=False
for i in range(len(primes)):
print(primes[i])