1. My original intention is to write a bottom-up merging algorithm, but it is too troublesome to give the head and tail coordinates or length of the subsequence segments of the sorting function every time, and whether the molecular sequence segments are odd or even. So I wonder if I can store the head and tail coordinates of each subsequence segment to be merged in advance, then pair them, delete the relevant information of the second subsequence segment in the merger, and adjust the tail coordinates of the first tone subsequence segment of the merger to represent the new subsequence segment after the merger. I want to use the linked list to store, but when I think of dividing two value fields to store the head and tail coordinates, if the array is large, the linked list should be at least as large as the array. Typically, space is used for time, and the conversion efficiency is still low. As shown in the figure:
2. So I want to change another idea. I only set one value field for each cell of the linked list to record the first coordinate of a sub sequence segment. Then, according to the fact that the sub sequence segments are adjacent, the first coordinate of the first sub sequence segment can be subtracted from the first coordinate of the second sub sequence segment to obtain the length of the first sub sequence segment, so that a sub sequence segment can be determined. By analogy, each subsequence segment can be determined. As shown in the figure:
3. But I found that this is easy to make mistakes, it is easy to confuse people, and special treatment should be given to the places marked yellow.
   Can you think of the number that the linked list should store after the second merger?
   This also takes up additional space. Although the position of the first and last elements of the subsequence to be merged next time can be obtained automatically, it is a little complex and error prone.
   Can we optimize it again and automatically get the position of the first and last elements of the subsequence to be merged each time without taking up additional space? So I want to find the law. As shown in the figure:
4. These subsequence segments marked in red have a feature (only part is marked), that is, they all participate in the merge sort, and finally sort by this, and the number of elements must be 2n. Why do you have to participate in the last sorting? Because the number of elements is 2n, these elements must be merged into a subsequence segment (in merge sort), and its number of elements must be greater than or equal to half of the array elements, which means that the sequence will participate in the last merge of merge sort. Because the number of elements is 2n power, it becomes very simple to find the head and tail coordinates of the two subsequences before and after the initial merging of these elements, and the length of the merged subsequence can be prepaid each time. This condition can be described as follows: K represents 2n, N represents the length of each merging of subsequences in the marked red section, and R represents the number of subsequences to be merged in each cycle. Satisfy K = N * R. However, because the comparison is carried out in pairs, it is impossible to merge an element by itself, so it should be changed to: R in practical application= (K / R) / 2. That is, R cannot be divided into 8 segments at the beginning. Then, if the coordinates of the subsequence are determined, the first subsequence starts from zero and the second is N. after a merge, both subsequences add N to represent the next two subsequences to be merged.
   The specific codes are as follows:

#include<stdio.h> 
#include<stdlib.h>
#define less(A,B) A<B
#define coswap if(less(A,B)){Item t = A;A = B;B = t}
void twosort(int a[],int b [] ,int N,int r)//Here, N is the number of elements to be sorted in each array, r is the number of arrays, and then the multiplication of these two numbers is equal to the total array length 
{
	//Because it is bottom-up, the number of elements to be compared each time is 2, but the part to be compared is 4 times. That is, this condition is met: the number of elements to be compared multiplied by the part to be compared is equal to the total number of elements of the array. 
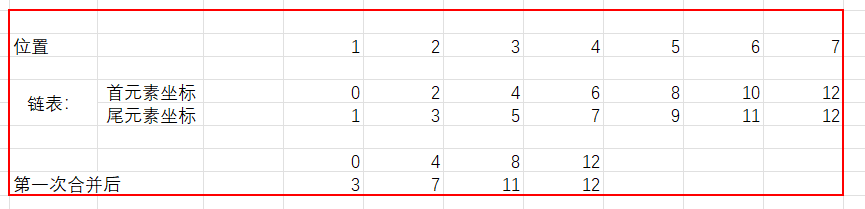
	int one = 0; //Represents the first element coordinate of the first subsequence 
	int two = N;//Represents the coordinates of the first element of the second array 
	int thr = 0;//Subscript array b 
	int cno ;//Counter of the first subsequence 
	int cnt ;	
	for(int i=0;i<r;i++){

		cnt = 0;
		cno = 0;
		printf("The first%d Coordinates of the second comparison:%d %d \n\n",i+1,one,two);
		while(cnt<N && cno<N){
		if(less(a[one],a[two])) {
			b[thr++] = a[one++]; 
			cno++;
		}
		else{
			b[thr++] = a[two++];
			cnt++;
		}
		}
		if(cnt>=N)while(cno<N){
			b[thr++] = a[one++];
			cno++;
		}else{
			while(cnt<N){
				b[thr++] = a[two++];
				cnt++; 
			}
		}
		one = one+N;//It should be noted that each time the traversal is completed, the number of comparison elements corresponding to the subscript displacement of the array in the first part is N; the same is true for the array elements in the second part 
		two = one + N;//There is no need to pass the superscript and subscript of each subsequence as before. 
		  for(int v=0;v<16;v++)printf(" %d ",b[v]);//This is convenient for inspection and can be deleted. 
		  printf("\n");
		   
	}		  	 
} 

void twofen(int a[],int b[],int K) 
{
	int r;
    for(int N = 1;N<K;N*= 2){
    	r = (K/N)/2;
    	twosort(a,b,N,r);
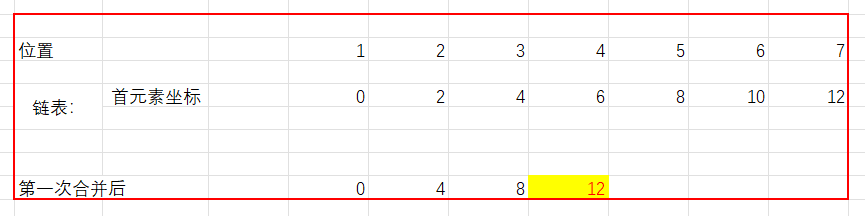
    	for(int i=0;i<16;i++)a[i] = b[i];//b before the last sort is ordered 
	}
	
}
int main()
{
	int a[16] = {1,5,3,7,2,6,4,9,11,10,22,15,16,13,25,19};
	int b[17] = {0};
	twofen(a,b,16);
	
}

1. In this way, we can easily complete the sorting of the first 2n elements. After thinking about it, we think that natural sorting is more appropriate, so we adopt natural sorting for the following elements. In this way, we will get two subsequence segments at the end, and then call the sorting function in natural sorting again, but pay attention to the lack of one copy, To change the positions of a and b, just change the natural sorting function a little. Then re glue the functional parts of the two sorting functions to get an improved natural sorting algorithm.
   The code is as follows

#include<stdio.h>
#include<stdlib.h>
#define key(A)  A
#define less(A,B) A<B
#define Number 29
int sort(int a[],int b[],int First,int Fnum,int Last,int Lnum)
{
	int i = First;
	while(Fnum>0 && Lnum > 0){//After the elements in a sequence are taken, another sequence element is added.
	
		if(less(a[First],a[Last])){
			b[i++] = a[First++];
			Fnum--;
		}else{
			b[i++] = a[Last++];
			Lnum--;
		}
	}	
	if(Fnum>0){
     	while(Fnum>0){
     		
       	b[i++] = a[First++];	
      	Fnum--;
	    }			
	}
	else{
		while(Lnum>0) {
			b[i++] = a[Last++];
			Lnum--;
		}
	}

}

void copy(int a[],int b[],int position)
{
	int i = position;
	int j = i;
	while(b[j]){
		a[i++] = b[j++];
	}
}

int huafen(int a[],int b[],int N,int position)//N is the subscript of the maximum element value in the array, and position is the starting position of scanning. 
{
    int First;//The first coordinate of the previous array 
    int Last;//The first coordinate of the next array
	int Fnum; //The number of elements that hold the first segment of the array 
	int Lnum;//The number of elements that hold the following array 
    int cnt = 1;//Counter
	int flag = 0;//Judge whether First is assigned 
	int Llag = 0;//Judge whether First is assigned 
	int segments = 1;

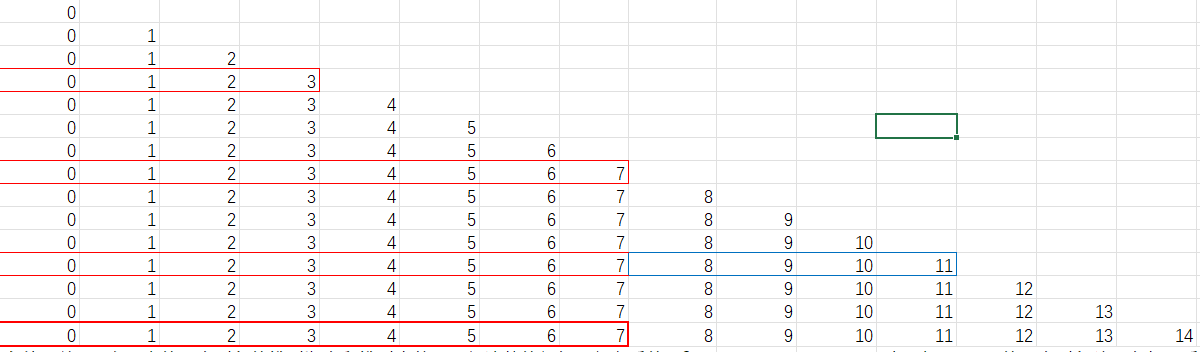
    for(int i=position;i<N;i++){	
    	if(less(a[i],a[i+1]) && i != N-1){
    		cnt++; 
		}
		else{	
			if(flag == 0 && i != N-1){
				First = i-cnt+1;//Add 1 here because cnt starts from 1, while First and Last start from 0			
				Fnum = cnt;			
				printf("\nFirst == %d  Fnum == %d\n",First,Fnum);	
				flag = 1;//Indicates that a value has been assigned 
				cnt = 1;//Restart counting 
				segments++;
			}else{				
				Last = i-cnt + 1;
				Lnum = cnt;				
				printf("\nLast == %d  Lnum == %d\n",Last,Lnum);	
				cnt = 1;//Re count 
				Llag = 1;
				segments++;
			} 
		if(Llag == 1 && flag == 1){
		sort(a,b,First,Fnum,Last,Lnum);
		flag = 0;//After sorting, the flag value is set to zero 
		Llag = 0;
		copy(a,b,First);			
		}
				
		}
			
	}
    return segments;
}

void AddNature(int a[],int b[],int N,int position)  
{
	int k = huafen(a,b,N,position); //When the array is merged for the first time, the number of subsequence segments is obtained at the same time. According to the number of subsequence segments, you can know how many times the array needs to be cycled
	int bour;
	int i=2;//Used to index the array when outputting 
	int Num = 0;  //Record how many scans are required 
	float segments = k;
	while(segments>1){
		segments = segments/2;
		bour = segments;
		if(segments > bour){//When the subsequence segments are odd, it is also prone to special cases, that is, the elements of the previous sequence are just smaller than those of the latter subsequence, which will be reduced virtually
		//An arrangement was made. 
			bour++;
			segments = bour;
		}
		Num++;
	} 
		
	for(int i=0;i<Num-1;i++){
	   huafen(a,b,N,position);
	}

}
//The above is the improved natural sorting array
//The following is an array for sorting 2^N elements
void twosort(int a[],int b[],int N,int r)//Here, N is the number of elements to be sorted in each array, r is the number of arrays, and then the multiplication of these two numbers is equal to the total array length 
{
	//Because it is bottom-up, the number of elements to be compared each time is 2, but the part to be compared is 4 times. That is, this condition is met: the number of elements to be compared multiplied by the part to be compared is equal to the total number of elements of the array. 
	int one = 0; 
	int two = N;
	int thr = 0;
	int cno ;
	int cnt ;	
	for(int i=0;i<r;i++){

		cnt = 0;
		cno = 0;
		printf("The first%d Coordinates of the second comparison:%d %d \n\n",i+1,one,two);
		while(cnt<N && cno<N){
		if(less(a[one],a[two])) {
			b[thr++] = a[one++]; 
			cno++;
		}
		else{
			b[thr++] = a[two++];
			cnt++;
		}
		}
		if(cnt>=N)while(cno<N){
			b[thr++] = a[one++];
			cno++;
		}else{
			while(cnt<N){
				b[thr++] = a[two++];
				cnt++; 
			}
		}
		one = one+N;//It should be noted that each time the traversal is completed, the number of comparison elements corresponding to the subscript displacement of the array in the first part is N; the same is true for the array elements in the second part 
		two = one + N;//There is no need to pass the superscript and subscript of each subsequence as before. 
		  for(int v=0;v<16;v++)printf(" %d ",b[v]);
		  printf("\n");
		   
	}		  	 
} 

void twofen(int a[],int b[],int K) 
{
	int r;
    for(int N = 1;N<K;N*= 2){
    	r = (K/N)/2;
    	twosort(a,b,N,r);
    	for(int i=0;i<16;i++)a[i] = b[i];//b before the last sort is ordered 
	}
	
} 
int main()
{
	int a[Number] = {20,1,10,3,6,9,5,36,78,96,23,19,64,28,99,45,12,5,24,44,56,23,32,54,76,54,49,39,67};
	int b[Number] = {0};
	int two = 1;
	for(;two<Number;two = two*2){		
	}
	two = two /2;
	twofen(a,b,two);
	AddNature(a,b,Number,two);
	int i=0;	
	int k=0;
	while(b[i])printf(" %d ",b[i++]);
	//Because a is missing a copy, here we switch the positions of a and b 
	sort(b,a,0,two,two,Number - two);
	printf("\n");
	while(a[k])printf(" %d ",a[k++]);


}

1. Summary: the essence of merge sort is pairwise sort. Understand the importance of the first 2n elements because it always participates in the last merge. In addition, dare to put your ideas into action. Before that, analyze whether the idea is reasonable to avoid wasting time.