Algorithm notes

Chapter 1: basic algorithm

1-1 sorting

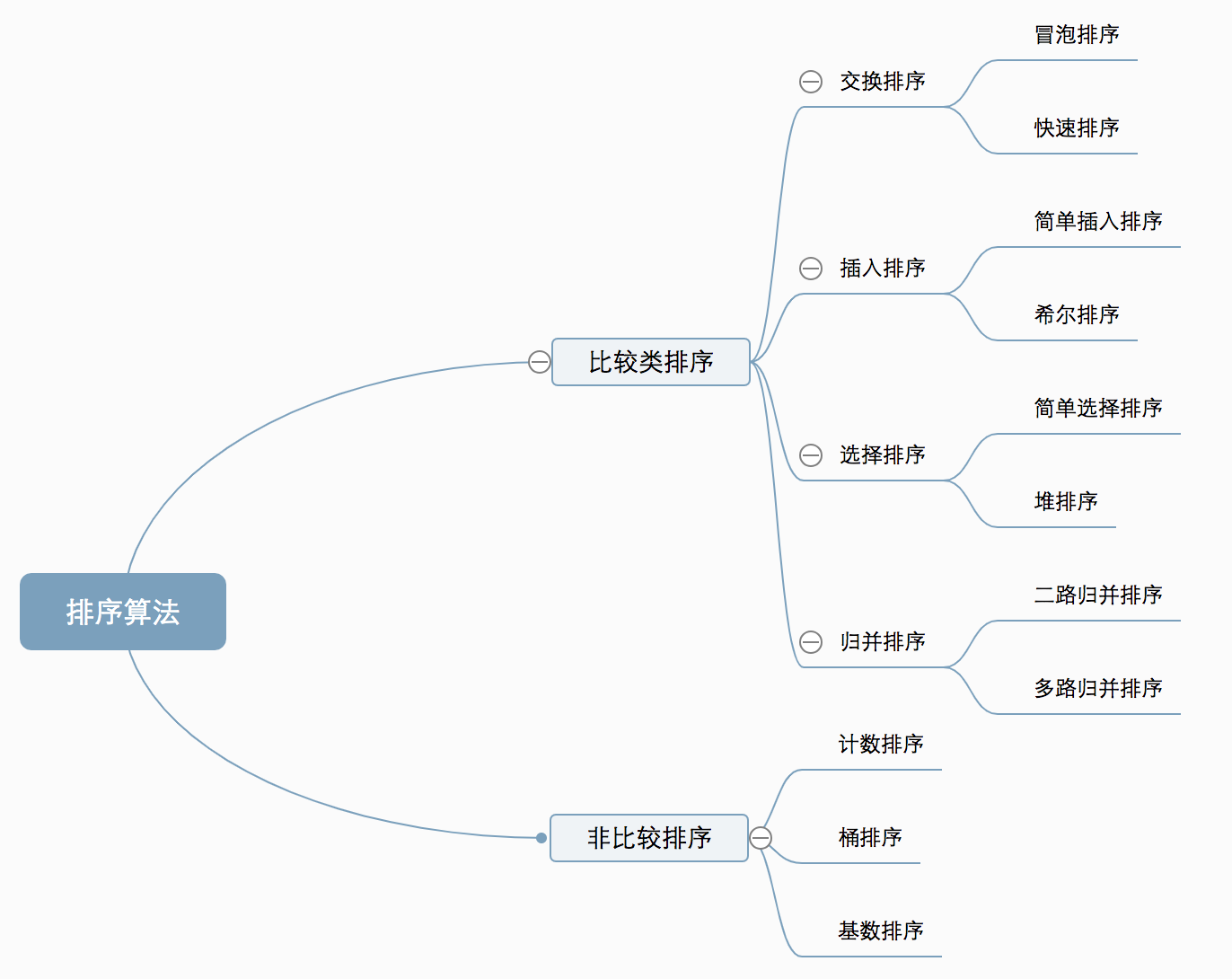
Algorithm classification
Ten common sorting algorithms can be divided into two categories:

• Comparison sort: the relative order between elements is determined by comparison. Because its time complexity cannot exceed O(nlogn), it is also called nonlinear time comparison sort.
• Non comparison sort: the relative order between elements is not determined by comparison. It can break through the lower bound of time based on comparison sort and run in linear time. Therefore, it is also called linear time non comparison sort.

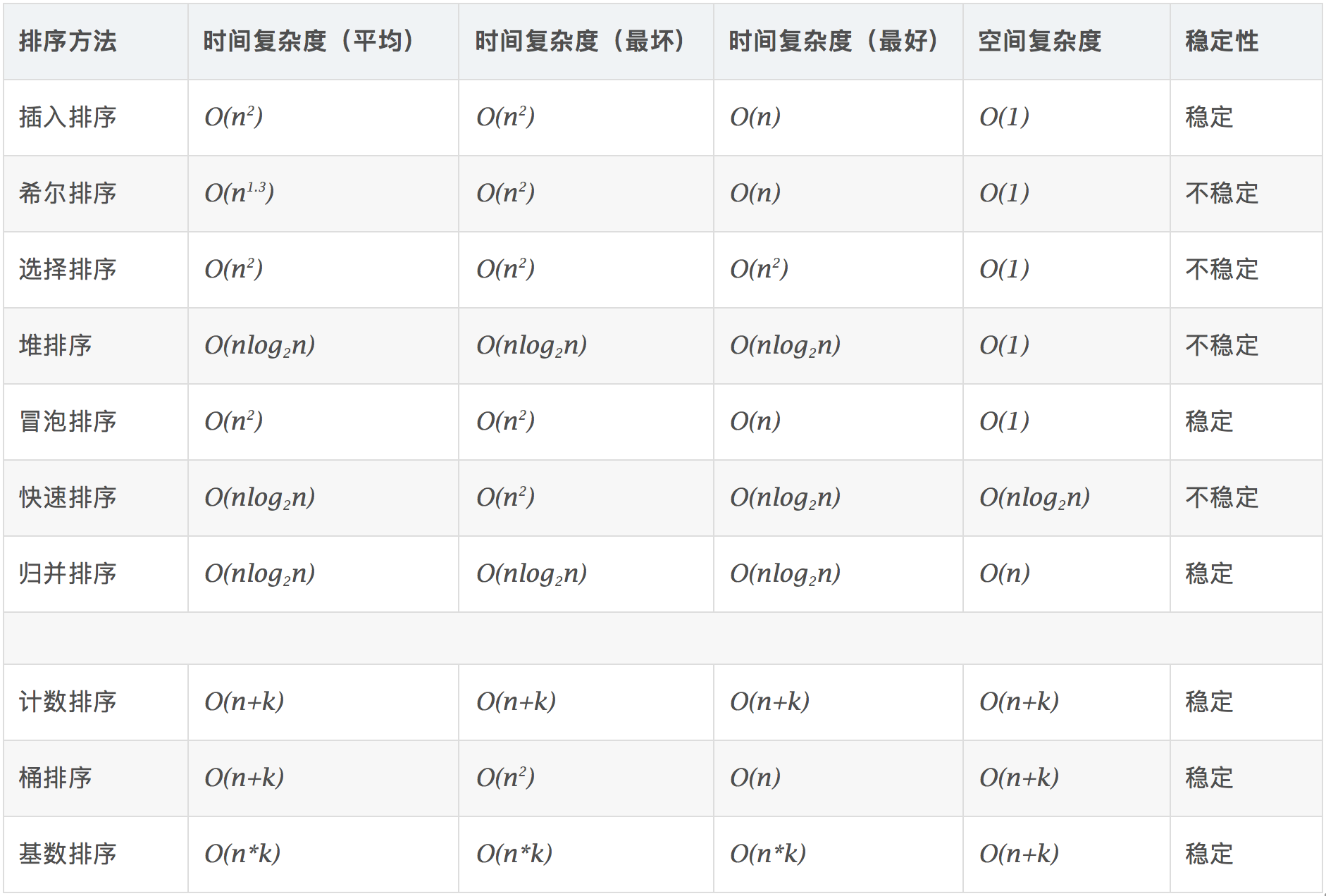
Time complexity diagram:

1-1-1 quick sort

Idea:

1. Determine the dividing point
   Given an x, make its array q divided into left and right segments
2. Adjust the interval to make it sort
   Let all the numbers on the left of X be less than or equal to x, and all the numbers on the right of X be greater than or equal to X
3. Recursion: continuous sorting
   Divide q[n] into n such paragraphs and repeat the above steps to sort

//Fast ascending template
void quick_sort(int l,int r)
{
    if(l>=r) return;//Stop when array q is recursive to an array length of 1
    
    int i=l-1,j=r+1;//Set two pointers to move
    int x=q[l+r>>1];//x is the dividing point
    while(i<j)//sort
    {
        while(q[++i]<x);//do i++; while(q[i]<x);
        while(q[--j]>x);//do j--; while(q[j)>x);
        if(i<j) swap(q[i],q[j]);//When the left and right sides of X stop, it means that the left side is less than X and the right side is greater than x. at this time, q[i] and q[j] are interchanged, and the while cycle can continue
    }
    //When the while loop ends, the condition that the left side of X is less than X and the right side of X is greater than x is met

	  //Recursive operation
	  //Recursion is carried out continuously. When the array recurses to the length of 3, it is determined that this array has monotonicity
    quick_sort(l,j);
    quick_sort(j+1,r);
    //After the recursion is completed, the array sorting is completed
}

Note: quick is called in the main function_ When sort function, expected

quick_sort(0,n-1);

Time complexity: O(nlogn)

1-1-2 merge sort

Idea: divide and rule

1. Determine the dividing point: take the intermediate value mid=(l+r)/2
2. Recursion: sorting both sides
3. Merge: merge two into one, compare the smaller value in the two paragraphs, and put it into the original array; If there is a value left in the last array, put it all into the original array

int q[N],tmp[N];
void merge_sort(int l,int r)
{
    if(l>=r) return;//Exit recursion
    
    int mid=(l+r)>>1;//Determine the dividing point and divide it into two sections
    int i=l,j=mid+1,k=0;
    
    merge_sort(l,mid);
    merge_sort(mid+1,r);
    
    while(i<=mid&&j<=r)//Compare the left and right paragraphs
        if(q[i]>=q[j]) tmp[k++]=q[j++];//If two segments have equal numbers at the same time, generally put the number of the first segment into tmp, because the merging sort is stable
        else tmp[k++]=q[i++];
        
    while(i<=mid) tmp[k++]=q[i++];//Section j is used up, and section i is put in
    while(j<=r) tmp[k++]=q[j++];//Section i is used up, and section j is put in
    
    for(int i=l,j=0;i<=r;i++) q[i]=tmp[j++];//Put the arranged data into the original array
}

Time complexity: O(nlogn)
More stable than fast platoon

1-2 binary search

• Binary search, also known as half search, is an efficient search method. However, the half search requires that the linear table must adopt the sequential storage structure, and the elements in the table are arranged in order by keywords

1-2-1 integer dichotomy

Idea:

1. Find the check function that can judge and determine the boundary point
2. The value of the given mid
3. Use the check function to determine whether the mid value should belong to the left boundary or the right boundary at the moment

void check_1(```)//Right satisfaction property

void check_2(```)//Left satisfaction property

int bsearch_1(int l,int r)//Take left boundary
{
    while(l<r)
    {
        int mid=l+r>>1;//mid is on the right half
        if(check_1) r=mid;
        else l=mid+1;
    }
    return l;
}

int bsearch_2(int l,int r)//Take right boundary
{
    while(l<r)
    {
        int mid=l+r+1>>1;//mid is on the left half
        if(check_2) l=mid;
        else r=mid-1
    }
    return l;
}

1-2-2 floating point binary

Idea: dichotomy with integer

//Code template
    while(r-l>=1e-8)//It is better to have a larger range e2 than the data given in the title, which is more accurate
    {
        mid=(l+r)/2;
        if(check) l=mid;
        else r=mid;
    }

1-3 high precision

• High precision algorithm is used to deal with the method of large calculation numbers in the computer. Because the storage length of a variable in the computer is limited, but it is easy for us to calculate large numbers of tens of billions or even hundreds of billions in the algorithm competition. At this time, we need to use high-precision algorithm. We take apart the large numbers, put them into the array one by one, and calculate them.

1-3-1 high precision addition

Thought: I think this method is very similar to the adder in the principle of computer composition

1. The idea of high-precision addition is similar to the calculation method of primary school. It starts from bit by bit and reduces it to simple single digit addition
2. Set a mark t to be stored in the result as the sum of two numbers

vector<int>add(vector<int>&A,vector<int>&B)
{
	vector<int>C;//Define an array c to store the result of adding two numbers
	
	int t=0;//t as a marker
	for(int i=0;i<A.size()||i<B.size();i++)//Because the length of array A and array B may be different, when one array is finished, the other array can be directly stored in the result C
	{
		if(i<A.size())t+=A[i];//If i is less than the length of A, store A in t
		if(i<B.size())t+=B[i];//Similarly
		C.push_back(t%10);//Put the one bit result of the addition of two numbers into C
		t/=10;//If t > 10, it means that carry is generated. Let t be equal to carry and participate in the operation of the next result
	}
	
	if(t)C.push_back(t);//When the last digit is calculated, t may generate carry. Since the two numbers are added, t can be directly put in
	return C;
}

1-3-2 high precision subtraction

Thought:

1. The idea of high-precision subtraction is similar to that of primary school subtraction. It also starts from the single digit and reduces it to a simple one digit subtraction
2. Similarly, a flag t is set to store the result of subtracting two numbers

vector <int> sub (vector<int> A,vector<int> B)
{
    vector <int> C;
    
    int t=0;
    
    for(int i=0;i<A.size();i++)
    {
        t+=A[i];
        if(i<B.size()) t-=B[i];
        
        C.push_back((t+10)%10);
        
        if(t<0) t=-1;
        else t=0;
    }
    
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;
}

be careful:

1. It shall be stored in reverse order when storing a and B, and output in reverse order when outputting C
2. Because it is subtraction, there is also the problem of comparing the length of a and B and the symbol

1-3-3 high precision multiplication (large number) × Decimal)

Thought:
1. It is also simulated by primary school multiplication, but different from addition and subtraction, b here is A decimal. Simplify A to one digit to multiply b
2. Similarly, set a variable t to store the result of multiplying one digit by b

#include<iostream>
#include<vector>
using namespace std;
vector<int> mul(vector<int>&A,int b)
{
    vector<int> C;
    int t=0;
    for(int i=0;i<A.size()||t;i++)
    {
        if(i<A.size())t+=A[i]*b;
        C.push_back(t%10);
        t/=10;
    }
    
    while(C.size()>1&&C.back()==0)C.pop_back();
    return C;
}
int main()
{
    string a;
    int b;
    cin>>a>>b;
    vector<int> A;
    for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    
    auto c=mul(A,b);
    
    for(int i=c.size()-1;i>=0;i--) cout<<c[i];
    
    return 0;
}

High precision Division

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
vector<int> div (vector<int>&A,int b,int &r)
{
    vector<int> C;
    
    for(int i=A.size()-1;i>=0;i--)
    {
        r=r*10+A[i];
        C.push_back(r/b);
        r%=b;
    }
    reverse(C.begin(),C.end());
    while(C.size()>1&&C.back()==0) C.pop_back();
    return C;
}
int main()
{
    string a;
    int b;
    cin>>a>>b;
    vector<int> A;
    for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    
    int r=0;
    auto c=div(A,b,r);
    
    for(int i=c.size()-1;i>=0;i--) cout<<c[i];
    cout<<endl<<r<<endl;
    return 0;
}

Part of the description of sorting comes from
Link: Ten classic sorting algorithms (dynamic graph demonstration)