brief introduction
The data structures of LinkedList and ArrayList are completely different. The bottom layer of ArrayList is the structure of array, while the bottom layer of LinkedList is the structure of linked list. It can carry out efficient insertion and removal operations. It is based on a two-way linked list structure.
Overall structure diagram of LinkedList
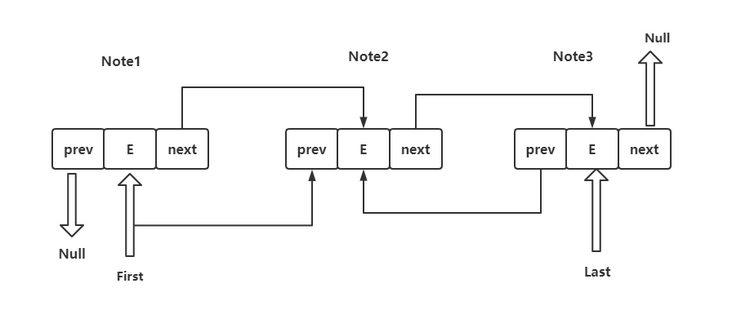
It can also be seen from the figure that LinkedList has many nodes, and the first and last variables store the information of the head and tail nodes; Also, it is not a circular two-way linked list, because it is null before and after. This is also what we need to pay attention to.
Inheritance system
public class LinkedList<E>
extends AbstractSequentialList<E>
implements List<E>, Deque<E>, Cloneable, java.io.Serializable
{...}Through the inheritance system, we can see that LinkedList not only implements the List interface, but also implements the Queue and Deque interfaces, so it can be used as a List, a double ended Queue and, of course, a stack.
Source code analysis
Main attributes
// Number of elements transient int size = 0; // First node of linked list transient Node<E> first; // End of list node transient Node<E> last;
Node node
private static class Node<E> {
//value
E item;
//Subsequent references to the next
Node<E> next;
//A precursor is a reference to a previous
Node<E> prev;
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}Construction method
public LinkedList() {
}
public LinkedList(Collection<? extends E> c) {
this();
//Insert all the elements in set C into the linked list
addAll(c);
}Add element
As a double ended queue, there are two main ways to add elements: one is to add elements at the end of the queue, and the other is to add elements at the head of the queue. These two forms are mainly realized in the LinkedList through the following two methods.
// Add element from queue header
private void linkFirst(E e) {
// Node head
final Node<E> f = first;
// Create a new node. The next node of the new node is the first node
final Node<E> newNode = new Node<>(null, e, f);
// Let the new node be the new first node
first = newNode;
// Determine whether it is the first element added
// If so, set last as the new node
// Otherwise, set the prev pointer of the original first node to the new node
if (f == null)
last = newNode;
else
f.prev = newNode;
// Number of elements plus 1
size++;
// The number of modifications plus 1 indicates that this is a set that supports fail fast
modCount++;
}
// Add element from end of queue
void linkLast(E e) {
// Queue tail node
final Node<E> l = last;
// Create a new node. The prev of the new node is the tail node
final Node<E> newNode = new Node<>(l, e, null);
// Make the new node the new tail node
last = newNode;
// Determine whether it is the first element added
// If yes, set first as the new node
// Otherwise, set the next pointer of the original tail node to the new node
if (l == null)
first = newNode;
else
l.next = newNode;
// Number of elements plus 1
size++;
// Number of modifications plus 1
modCount++;
}
public void addFirst(E e) {
linkFirst(e);
}
public void addLast(E e) {
linkLast(e);
}
// As an unbounded queue, adding elements will always succeed
public boolean offerFirst(E e) {
addFirst(e);
return true;
}
public boolean offerLast(E e) {
addLast(e);
return true;
}The above is a double ended queue. Its added elements are divided into the first and last added elements. As a List, it is necessary to support the addition of elements in the middle, mainly through the following method.
// Add element before node succ
void linkBefore(E e, Node<E> succ) {
// succ is the successor node of the node to be added
// Find the front node of the node to be added
final Node<E> pred = succ.prev;
// Create a new node between its predecessor and successor
final Node<E> newNode = new Node<>(pred, e, succ);
// Modify the leading pointer of the subsequent node to point to the new node
succ.prev = newNode;
// Judge whether the front node is empty
// If it is empty, it indicates that it is the first added element. Modify the first pointer
// Otherwise, modify the next of the front node to a new node
if (pred == null)
first = newNode;
else
pred.next = newNode;
// Number of modified elements
size++;
// Number of modifications plus 1
modCount++;
}
// Find the node at index location
Node<E> node(int index) {
// Because it's a double linked list
// Therefore, whether to traverse from the front or from the back depends on whether the index is in the first half or the second half
// In this way, the index can traverse half of the elements in the second half
if (index < (size >> 1)) {
// If it's in the first half
// Just traverse the past
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {
// If it's in the second half
// Just traverse from the back
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
// Adds an element at the specified index location
public void add(int index, E element) {
// Judge whether the boundary is crossed
checkPositionIndex(index);
// If the index is a position after the end node of the queue
// Add the new node directly after the tail node
// Otherwise, call the linkBefore() method to add nodes in the middle
if (index == size)
linkLast(element);
else
linkBefore(element, node(index));
}The method of adding elements in the middle is also very simple. The typical method of adding elements in the middle of double linked list.
The three ways to add elements are roughly as shown in the following figure:
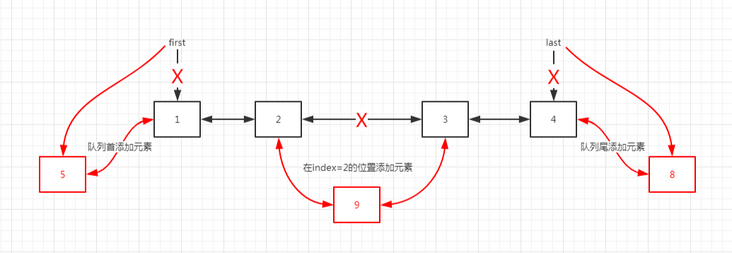
Adding elements at the beginning and end of the queue is very efficient, and the time complexity is O(1).
Adding elements in the middle is inefficient. First, find the node at the insertion position, and then modify the pointer of the front and rear nodes. The time complexity is O(n).
Delete element
As a double ended queue, there are two ways to delete elements. One is to delete elements at the beginning of the queue, and the other is to delete elements at the end of the queue.
As a List, it also supports deleting elements in the middle, so there are three methods to delete elements, as follows.
// Delete first node
private E unlinkFirst(Node<E> f) {
// Element value of the first node
final E element = f.item;
// next pointer of the first node
final Node<E> next = f.next;
// Add the content of the first node to assist GC
f.item = null;
f.next = null; // help GC
// Take the next of the first node as the new first node
first = next;
// If only one element is deleted, set it to empty
// Otherwise, set the leading pointer of next to null
if (next == null)
last = null;
else
next.prev = null;
// Number of elements minus 1
size--;
// Number of modifications plus 1
modCount++;
// Returns the deleted element
return element;
}
// Delete tail node
private E unlinkLast(Node<E> l) {
// Element value of tail node
final E element = l.item;
// Leading pointer of tail node
final Node<E> prev = l.prev;
// Clear the contents of the tail node and assist the GC
l.item = null;
l.prev = null; // help GC
// Make the front node the new tail node
last = prev;
// If there is only one element, delete and set first to null
// Otherwise, set the next of the preceding node to null
if (prev == null)
first = null;
else
prev.next = null;
// Number of elements minus 1
size--;
// Number of modifications plus 1
modCount++;
// Returns the deleted element
return element;
}
// Delete specified node x
E unlink(Node<E> x) {
// Element value of x
final E element = x.item;
// Front node of x
final Node<E> next = x.next;
// Post node of x
final Node<E> prev = x.prev;
// If the front node is empty
// The description is the first node. Let first point to the post node of x
// Otherwise, modify the post node whose next of the front node is x
if (prev == null) {
first = next;
} else {
prev.next = next;
x.prev = null;
}
// If the post node is empty
// The description is the tail node. Let last point to the front node of x
// Otherwise, modify the pre node whose prev is x of the post node
if (next == null) {
last = prev;
} else {
next.prev = prev;
x.next = null;
}
// Clear the element value of x to assist GC
x.item = null;
// Number of elements minus 1
size--;
// Number of modifications plus 1
modCount++;
// Returns the deleted element
return element;
}
// If there is no element during remove, an exception will be thrown
public E removeFirst() {
final Node<E> f = first;
if (f == null)
throw new NoSuchElementException();
return unlinkFirst(f);
}
// If there is no element during remove, an exception will be thrown
public E removeLast() {
final Node<E> l = last;
if (l == null)
throw new NoSuchElementException();
return unlinkLast(l);
}
// poll returns null if there is no element
public E pollFirst() {
final Node<E> f = first;
return (f == null) ? null : unlinkFirst(f);
}
// poll returns null if there is no element
public E pollLast() {
final Node<E> l = last;
return (l == null) ? null : unlinkLast(l);
}
// Delete intermediate node
public E remove(int index) {
// Check whether it is out of bounds
checkElementIndex(index);
// Delete the node at the specified index location
return unlink(node(index));
}The three methods of deleting elements are typical double linked list methods. The general process is shown in the figure below.
[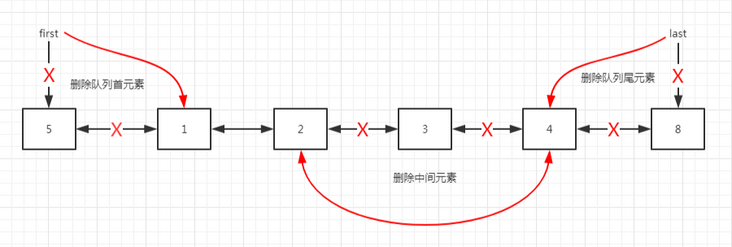
It is efficient to delete elements at the beginning and end of the queue, and the time complexity is O(1).
It is inefficient to delete elements in the middle. First find the node at the deletion position, and then modify the front and back pointers. The time complexity is O(n).
Stack
As we said earlier, LinkedList is a double ended queue. Remember that the double ended queue can be used as a stack?
package org.example.test;
import java.util.LinkedList;
/**
* Using LinkedList to simulate stack
* Stack features: first in and last out
*/
public class Test12 {
private LinkedList<String> linkList = new LinkedList<String>();
// Stack pressing
public void push(String str){
linkList.addFirst(str);
}
// Out of stack
public String pop(){
return linkList.removeFirst();
}
// see
public String peek(){
return linkList.peek();
}
// Judge whether it is empty
public boolean isEmpty(){
return linkList.isEmpty();
}
}
class Test13 {
public static void main(String[] args) {
// Test stack
Test12 test12 = new Test12();
test12.push("I was the first to go in");
test12.push("I was the second to go in");
test12.push("I was the third to go in");
test12.push("I was the fourth to go in");
test12.push("I was the fifth to go in");
// take out
while (!test12.isEmpty()){
String pop = test12.pop();
System.out.println(pop);
}
// Print results
/*I was the fifth to go in
I was the fourth to go in
I was the third to go in
I was the second to go in
I was the first to go in*/
}
}The stack feature is LIFO(Last In First Out), so it is also very simple to use as a stack. Adding and deleting elements only operate on the first node of the queue.
summary
(1) LinkedList is a List implemented by double linked List, so there is no problem of insufficient capacity, so there is no method of capacity expansion.
(2) LinkedList is also a double ended queue, which has the characteristics of queue, double ended queue and stack.
(3) LinkedList is very efficient in adding and deleting elements at the beginning and end of the queue, and the time complexity is O(1).
(4) LinkedList is inefficient to add and delete elements in the middle, and the time complexity is O(n).
(5) LinkedList does not support random access, so it is inefficient to access non queue elements.
(6) LinkedList is functionally equal to ArrayList + ArrayDeque.
(7) LinkedList is non thread safe.
(8) LinkedList can store null values.
Classic interview questions
Talk about the difference between ArrayList and LinkedList.
The essential difference comes from the bottom implementation of the two: the bottom of ArrayList is array, and the bottom of LinkedList is bidirectional linked list.
The array has the query efficiency of O(1) and can directly locate elements through subscripts; The linked list can only be queried by traversal when querying elements, which is less efficient than array.
The efficiency of adding and deleting elements in the array is relatively low, which is usually accompanied by the operation of copying the array; The efficiency of adding and deleting elements in the linked list is very high. You only need to adjust the pointer at the corresponding position.
The above is a popular comparison between arrays and linked lists. In daily use, both can play a good role in their own applicable scenarios.
We often use ArrayList instead of array, because it encapsulates many easy-to-use APIs and implements the automatic capacity expansion mechanism. Because it internally maintains a pointer size of the current capacity, the time complexity of directly adding elements to ArrayList is O(1), which is very convenient to use.
LinkedList is often used as the implementation class of Queue queue. Because the bottom layer is a two-way linked list, it can easily provide first in first out operations.
It can be divided into two parts: one is the difference between the underlying implementation of array and linked list, and the other is the implementation details of ArrayList and LinkedList.