Recently, I started to learn go. The company also arranged some corresponding exercises, including those related to binary tree. I happened to pick up some knowledge points in this regard
In the computer data structure, we often come into contact with the typical nonlinear data structure of tree. The following picture shows a standard tree structure
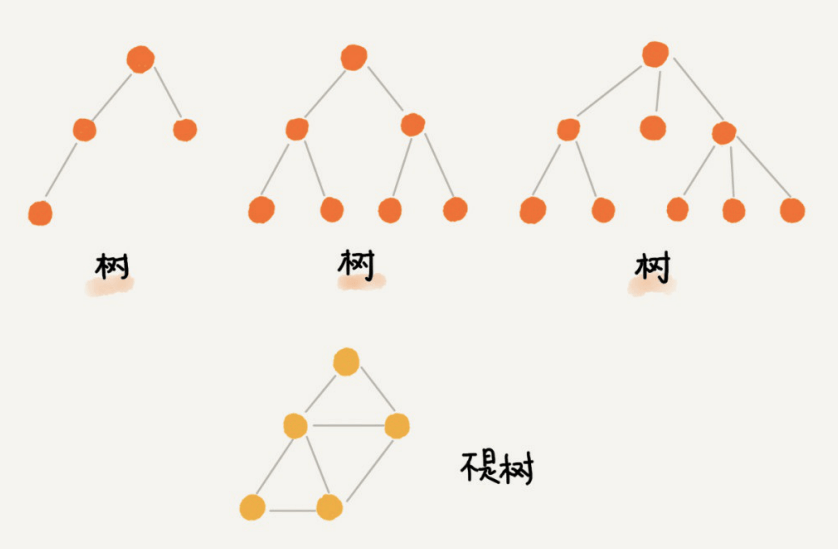
In the data structure, the tree is defined as follows.
A tree is a finite set of n (n > = 0) nodes. When n=0, it is called an empty tree. In any non empty tree, it has the following characteristics.
- There is and only one specific node called root
- When n > 1, the other nodes can be divided into m (M > 0) disjoint finite sets. Each set itself is a tree and is called the subtree of the root
What is a binary tree
Binary tree is a characteristic form of tree. Binary, as the name suggests, each node of this tree has at most 2 word nodes. Note that there are at most 2 nodes, maybe only 1, or no child nodes.
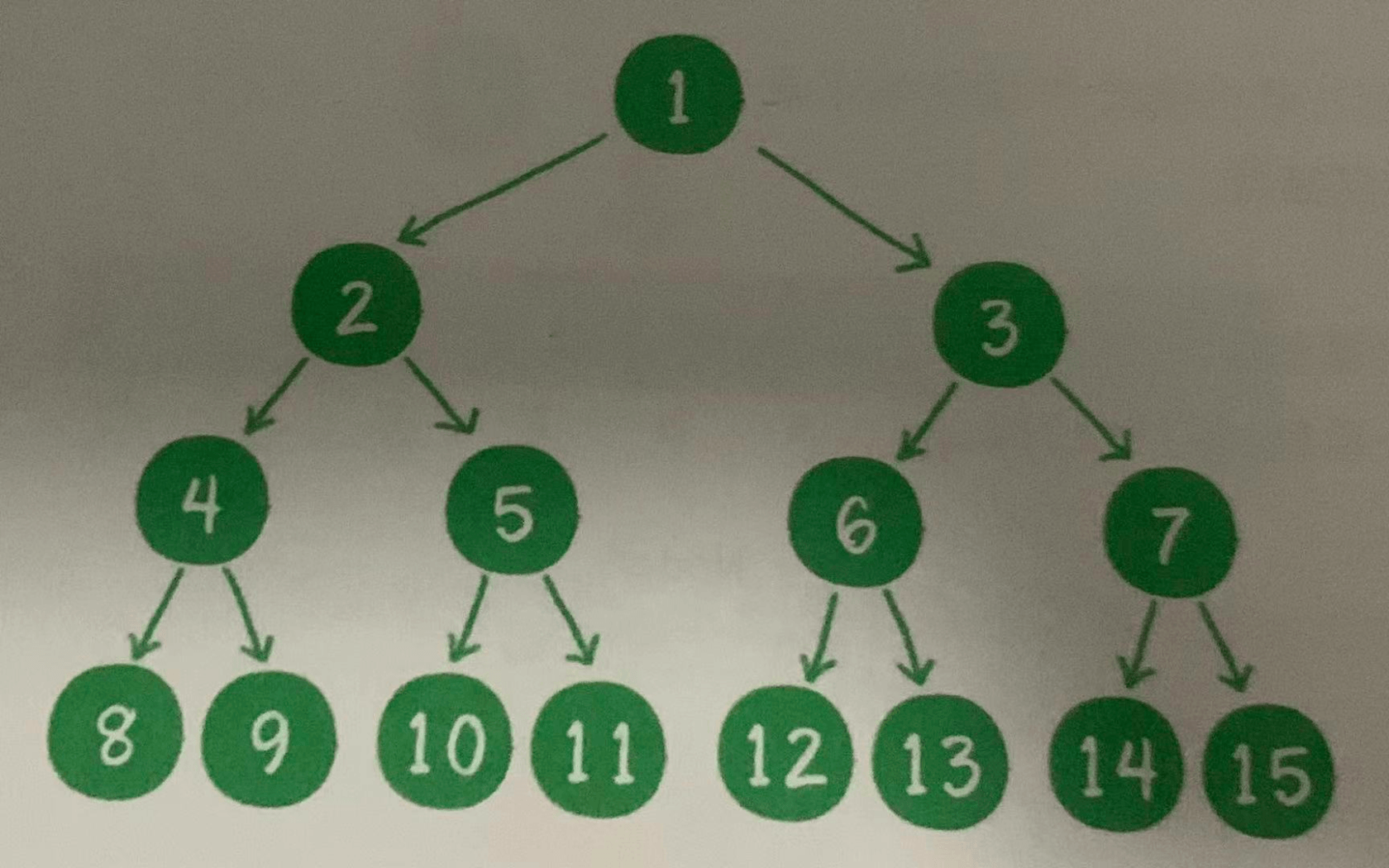
Binary tree has two special forms, one is called full binary tree, the other is called complete binary tree
If all non leaf nodes of a binary tree have left and right nodes, and all leaf nodes are at the same level, the tree is a full binary tree. As shown in the figure below
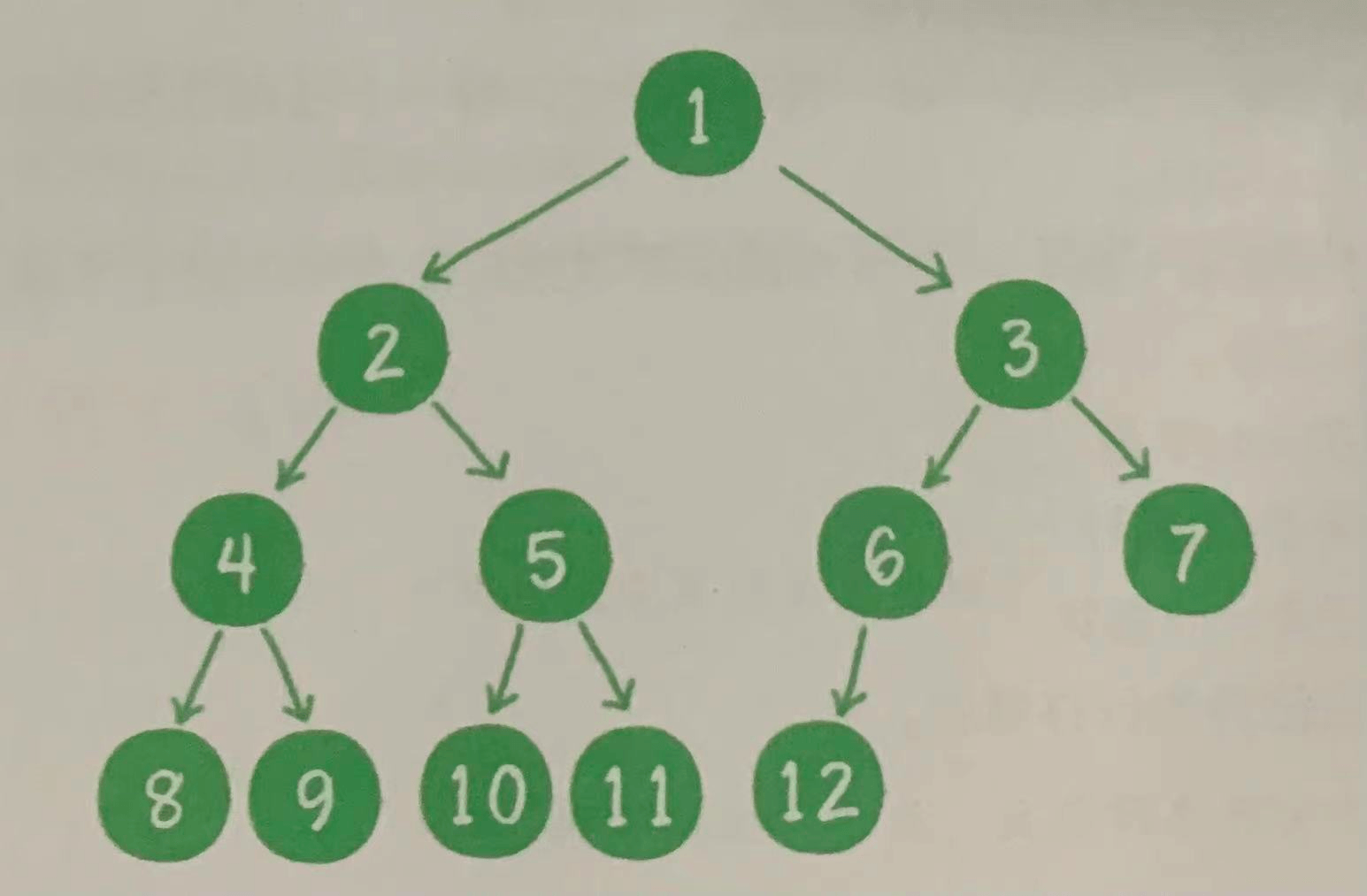
If a binary tree with n nodes is numbered in hierarchical order, the numbers of all nodes are 1 to n. If all nodes of the tree are in the same position as the nodes numbered 1 to n of the full binary tree with the same depth, the binary tree is a complete binary tree. As shown in the figure below
Traversal of binary tree
After introducing the concept of binary tree, we begin to practice. Binary tree is a typical nonlinear data structure. When traversing, we need to convert the nonlinear associated nodes into a linear sequence, which can be traversed in different ways, and the traversal sequence is also different.
From the point of view of the location relationship between nodes, the traversal of binary tree is divided into four kinds.
1. Preorder traversal
2. Zhongshun traversal
3. Post order traversal
4. Sequence traversal
From a more macro point of view, the traversal of binary trees can be divided into two categories
1. Depth first traversal (pre order traversal, middle order traversal, post order traversal)
2. Breadth first traversal (sequence traversal)
Depth first traversal
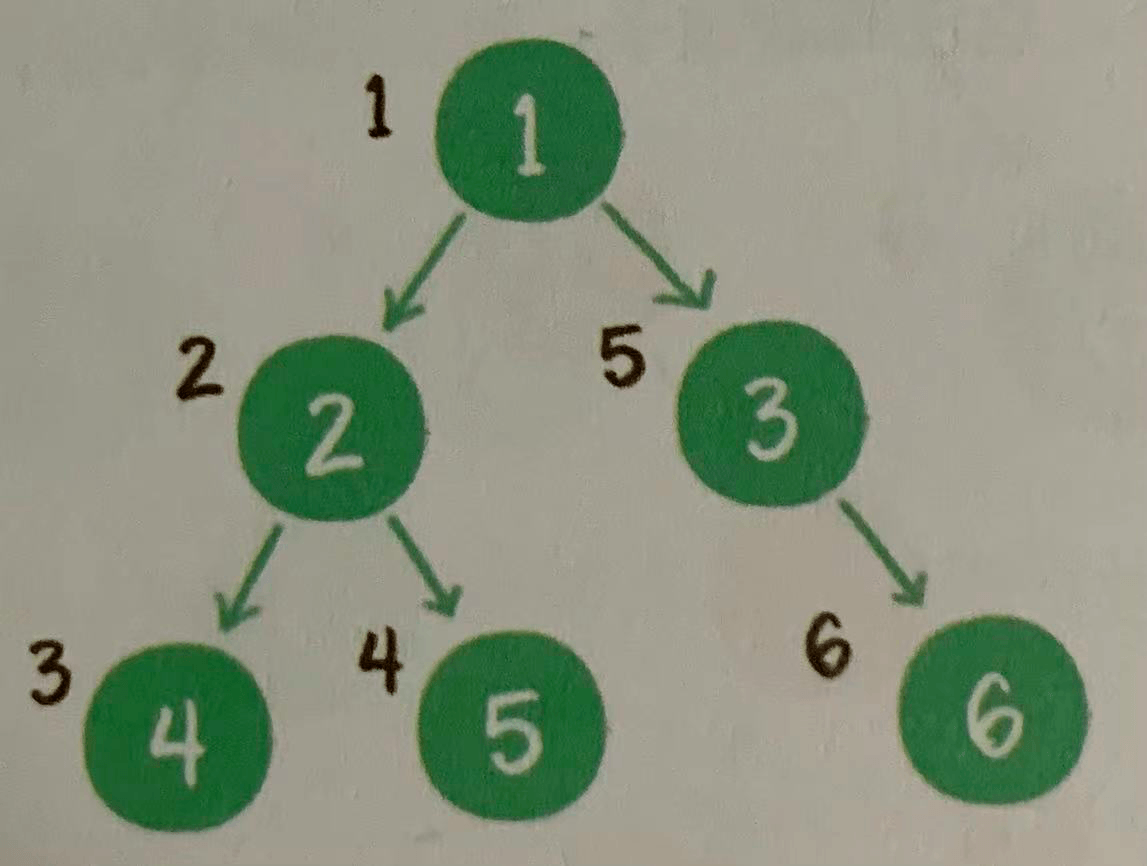
1. Preorder traversal
Before traversing the binary tree, the output order is the root node, left subtree and right subtree. As shown in the figure below
The code is implemented as follows
package main
import (
"fmt"
)
//Define a binary tree structure
type binaryTree struct {
value int
leftNode *binaryTree
rightNode *binaryTree
}
func main(){
//0 means the node is empty
num := []int{1,2,3,4,5,0,6}
//Convert array slices into binary tree structures
tree := createBinaryTree(0,num)
//Binary tree data
var front []int
front = frontForeach(*tree,front)
fmt.Println(front)
}
//Create binary tree
func createBinaryTree(i int,nums []int) *binaryTree {
tree := &binaryTree{nums[i], nil, nil}
//The array subscript of the left node is 1,3,5 2*i+1
if i<len(nums) && 2*i+1 < len(nums) {
tree.leftNode = createBinaryTree(2*i+1, nums)
}
//The array subscript of the right node is 2,4,6 2*i+2
if i<len(nums) && 2*i+2 < len(nums) {
tree.rightNode = createBinaryTree(2*i+2, nums)
}
return tree
}
//Preorder traversal
func frontForeach(tree binaryTree,num []int) []int{
//Traverse the root node first
if tree.value != 0 {
num = append(num,tree.value)
}
var leftNum,rightNum []int
//If there is a left node, traverse the left node tree
if tree.leftNode != nil {
leftNum = frontForeach(*tree.leftNode,leftNum)
for _,value := range leftNum{
num = append(num,value)
}
}
//If there is a right node, traverse the right node tree
if tree.rightNode != nil {
rightNum = frontForeach(*tree.rightNode,rightNum)
for _,value := range rightNum{
num = append(num,value)
}
}
return num
}2. Middle order traversal
The middle order traversal of binary tree, and the output order is left subtree, root node and right subtree. As shown in the figure below
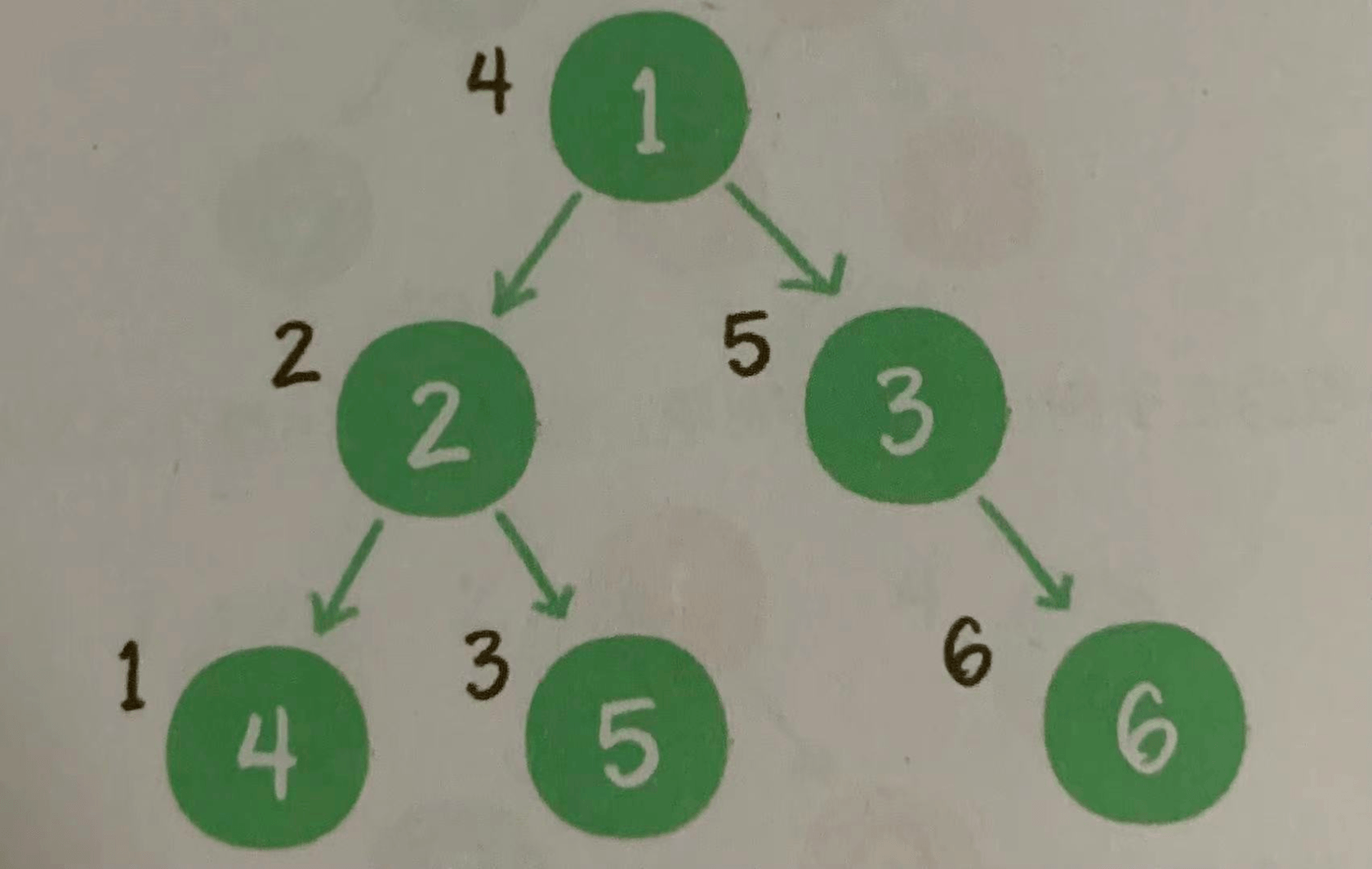
package main
import (
"fmt"
)
//Define a binary tree structure
type binaryTree struct {
value int
leftNode *binaryTree
rightNode *binaryTree
}
func main(){
//0 means the node is empty
num := []int{1,2,3,4,5,0,6}
tree := createBinaryTree(0,num)
//Binary tree data
var middle []int
middle = middleForeach(*tree,middle)
fmt.Println(middle)
}
//Create binary tree
func createBinaryTree(i int,nums []int) *binaryTree {
tree := &binaryTree{nums[i], nil, nil}
//The array subscript of the left node is 1,3,5 2*i+1
if i<len(nums) && 2*i+1 < len(nums) {
tree.leftNode = createBinaryTree(2*i+1, nums)
}
//The array subscript of the right node is 2,4,6 2*i+2
if i<len(nums) && 2*i+2 < len(nums) {
tree.rightNode = createBinaryTree(2*i+2, nums)
}
return tree
}
//Medium order traversal
func middleForeach(tree binaryTree,num []int) []int{
var leftNum,rightNum []int
//If there is a left node, traverse the left node tree
if tree.leftNode != nil {
leftNum = middleForeach(*tree.leftNode,leftNum)
for _,value := range leftNum{
num = append(num,value)
}
}
//Traverse the root node first
if tree.value != 0 {
num = append(num,tree.value)
}
//If there is a right node, traverse the right node tree
if tree.rightNode != nil {
rightNum = middleForeach(*tree.rightNode,rightNum)
for _,value := range rightNum{
num = append(num,value)
}
}
return num
}
3. Post order traversal
After traversing the binary tree, the output order is left subtree, right subtree and root node. As shown in the figure below
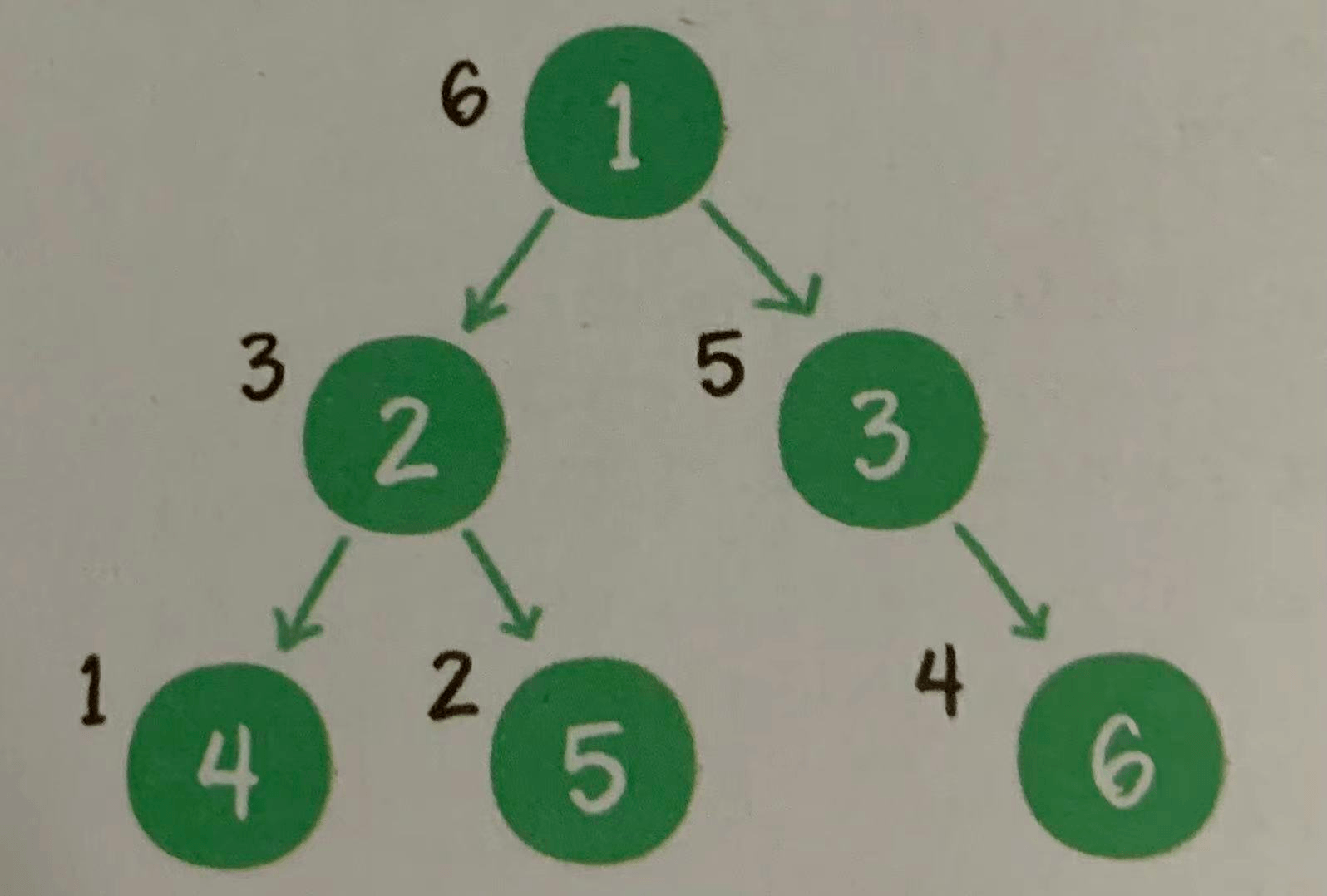
package main
import (
"fmt"
)
//Define a binary tree structure
type binaryTree struct {
value int
leftNode *binaryTree
rightNode *binaryTree
}
func main(){
//0 means the node is empty
num := []int{1,2,3,4,5,0,6}
tree := createBinaryTree(0,num)
//Binary tree data
var behind []int
behind = behindForeach(*tree,behind)
fmt.Println(behind)
}
//Create binary tree
func createBinaryTree(i int,nums []int) *binaryTree {
tree := &binaryTree{nums[i], nil, nil}
//The array subscript of the left node is 1,3,5 2*i+1
if i<len(nums) && 2*i+1 < len(nums) {
tree.leftNode = createBinaryTree(2*i+1, nums)
}
//The array subscript of the right node is 2,4,6 2*i+2
if i<len(nums) && 2*i+2 < len(nums) {
tree.rightNode = createBinaryTree(2*i+2, nums)
}
return tree
}
//Postorder traversal
func behindForeach(tree binaryTree,num []int) []int{
var leftNum,rightNum []int
//If there is a left node, traverse the left node tree
if tree.leftNode != nil {
leftNum = behindForeach(*tree.leftNode,leftNum)
for _,value := range leftNum{
num = append(num,value)
}
}
//If there is a right node, traverse the right node tree
if tree.rightNode != nil {
rightNum = behindForeach(*tree.rightNode,rightNum)
for _,value := range rightNum{
num = append(num,value)
}
}
//Traverse the root node first
if tree.value != 0 {
num = append(num,tree.value)
}
return num
}
The above three traversal methods are relatively simple, and the traversal order can be completed only during the traversal process. Let's look at another way of traversal.
breadth-first search
level traversal
As the name suggests, the binary tree traverses each node horizontally layer by layer according to the hierarchical relationship from root node to leaf node, as shown below
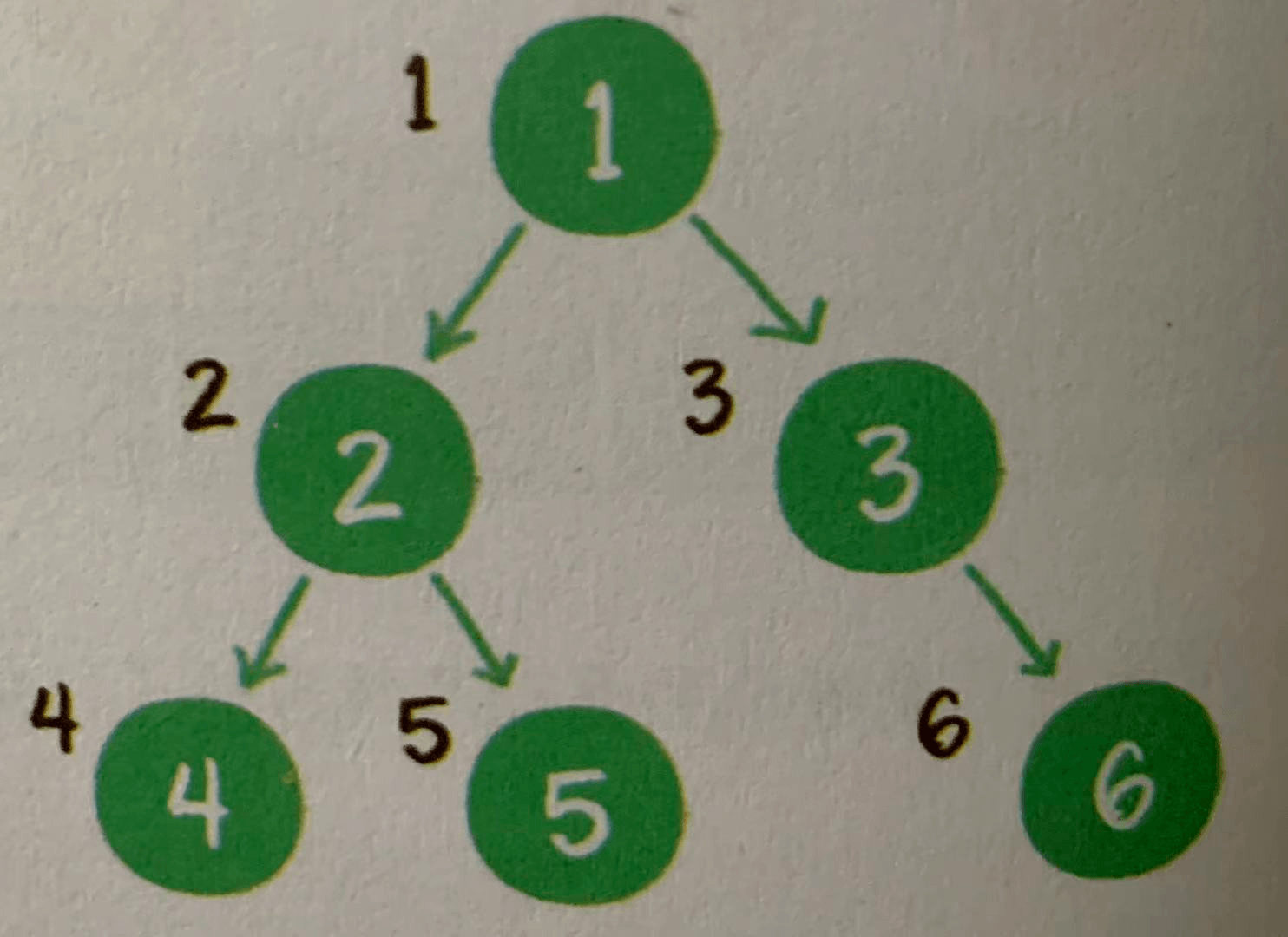
In terms of code implementation, it is different from depth first traversal. Instead of using recursion, it uses queue. In the traversal process, it completes sequence traversal by adding queue and reading queue head
package main
import (
"fmt"
)
//Define a binary tree structure
type binaryTree struct {
value int
leftNode *binaryTree
rightNode *binaryTree
}
func main(){
//0 means the node is empty
num := []int{1,2,3,4,5,0,6}
tree := createBinaryTree(0,num)
//Binary tree data
var row []int
row = rowForeach(*tree,row)
fmt.Println(row)
}
//Create binary tree
func createBinaryTree(i int,nums []int) *binaryTree {
tree := &binaryTree{nums[i], nil, nil}
//The array subscript of the left node is 1,3,5 2*i+1
if i<len(nums) && 2*i+1 < len(nums) {
tree.leftNode = createBinaryTree(2*i+1, nums)
}
//The array subscript of the right node is 2,4,6 2*i+2
if i<len(nums) && 2*i+2 < len(nums) {
tree.rightNode = createBinaryTree(2*i+2, nums)
}
return tree
}
//level traversal
func rowForeach(tree binaryTree,num []int) []int {
//Define queue
var queue []binaryTree
queue = append(queue,tree)
for len(queue) > 0{
var first binaryTree
first = queue[0]
if first.value != 0 {
//Take out the team head value
num = append(num,first.value)
}
//Delete team leader
queue = queue[1:]
//If the left node exists, join the tail of the queue
if first.leftNode != nil {
queue = append(queue,*first.leftNode)
}
//If the right node exists, join the tail of the queue
if first.rightNode != nil {
queue = append(queue,*first.rightNode)
}
}
return num
}
Binary reactor
Binary heap is essentially a complete binary tree, which is divided into two types
1. Maximum heap: any parent node of the large top heap is greater than or equal to the value of its left and right child nodes, as shown in the following figure
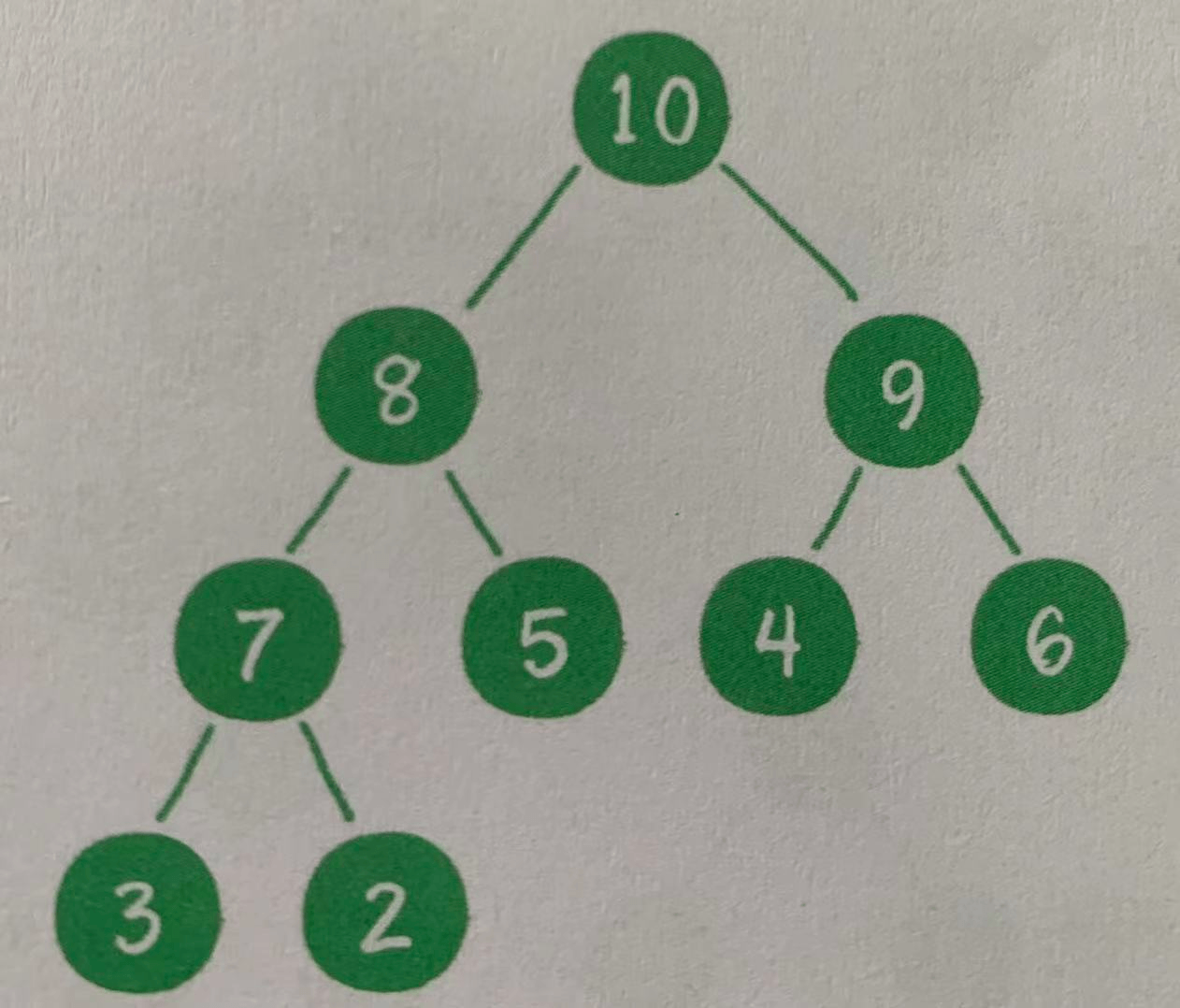
2. Minimum heap: any parent node of the small top heap is less than or equal to the value of its left and right child nodes, as shown in the following figure
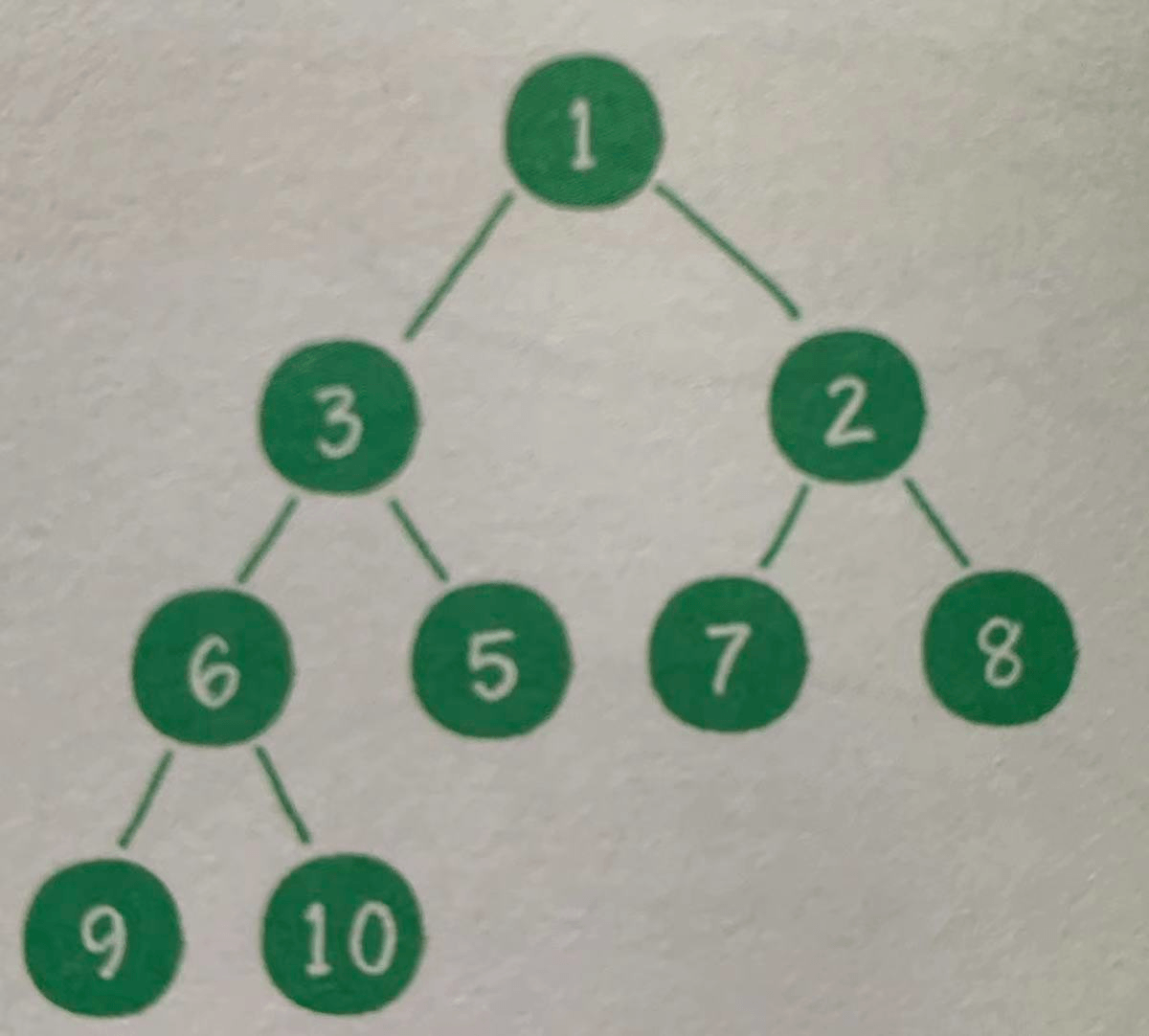
The root node of a binary heap is called the top of the heap. The characteristics of maximum heap and minimum heap determine that the top of the maximum heap is the largest element in the whole heap; The smallest heap is the smallest element in the whole heap.
For binary heap, there are several operations as follows
1. Insert node
2. Delete node
3. Construct binary tree
In terms of code implementation, since the heap is a complete binary tree, array can be used for storage. Assuming that the subscript of the parent node is parent, its left child subscript is 2 * parent+1 and its right child subscript is 2 * parent+2
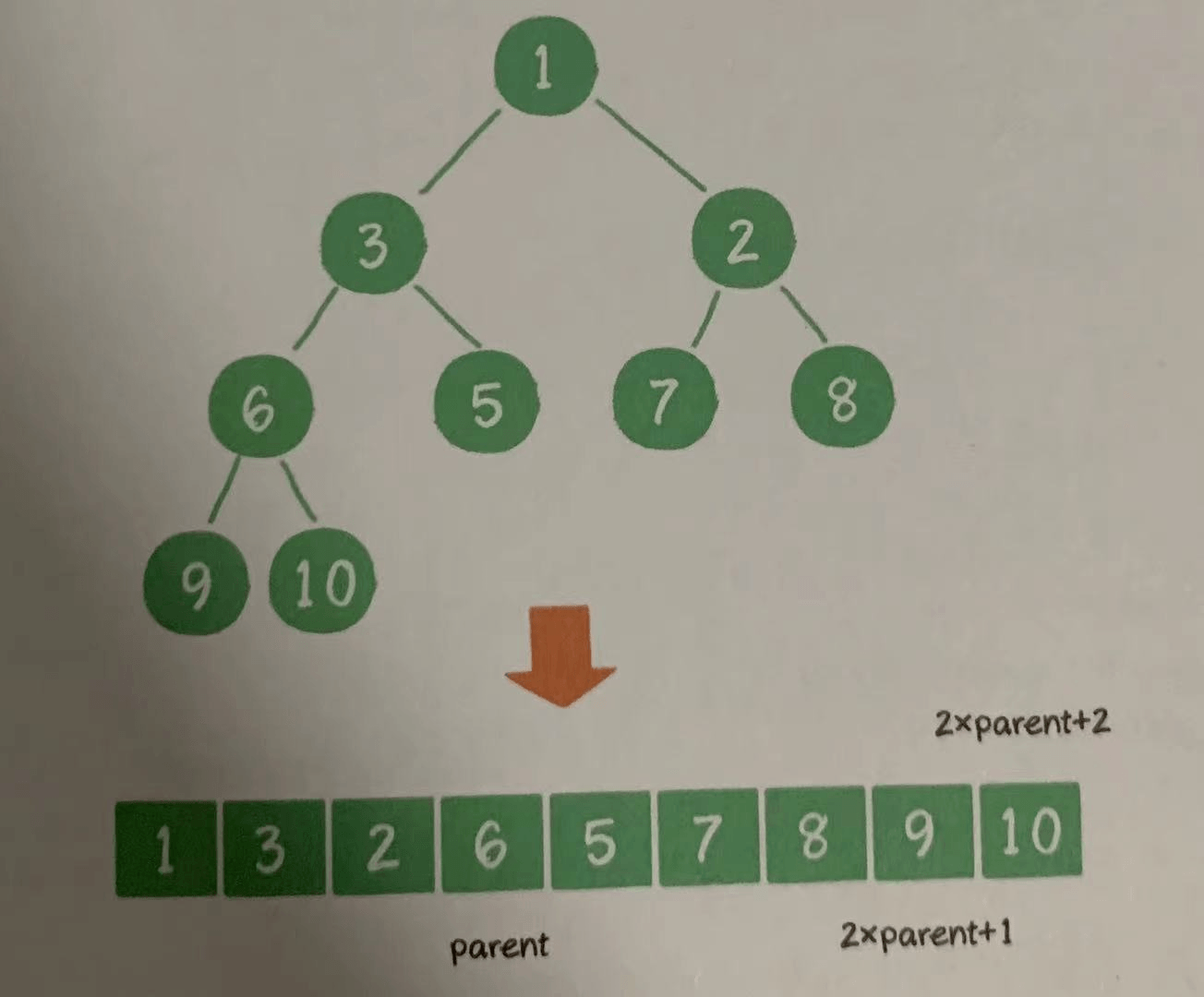
The code for constructing the maximum heap is as follows: the implementation idea is roughly to find the nearest non leaf node first. Assuming there are n nodes, the nearest non leaf node is n/2. Judge each node to determine whether the node is greater than the root node. If not, the node sinks. Through step-by-step cyclic judgment, a maximum heap is constructed
package main
import "fmt"
func main(){
var numArr = []int{2,8,23,4,5,77,65,43}
buildMaxHeap(numArr,len(numArr))
fmt.Print(numArr)
}
//Build maximum heap
func buildMaxHeap(arr []int,arrLen int){
for i := arrLen/2;i >= 0; i-- {
sink(arr,i,arrLen)
}
}
//Tree node value sinking judgment
func sink(arr []int,i,arrLen int) {
//Left node subscript
left := i*2+1
//Right node subscript
right := i*2+2
largest := i
//If the left node is larger than the parent node, the value is exchanged
if left < arrLen && arr[left] > arr[largest] {
largest = left
}
if right < arrLen && arr[right] > arr[largest] {
largest = right
}
//The node value is greater than the parent node value, and data exchange is required
if largest != i {
//Exchange value
swap(arr,i,largest)
//After the exchange is completed, continue to judge whether the exchanged node value needs to continue to sink
sink(arr,largest,arrLen)
}
}
//change of position
func swap(arr []int,i,j int) {
arr[i],arr[j] = arr[j],arr[i]
}
Priority queue
Queues are characterized by first in first out (FIFO)
Enter the queue and place the new element at the end of the queue; Out of the queue, the queue head element is removed first;
The priority queue no longer follows the principle of first in first out, but is divided into two cases.
- The maximum priority queue, regardless of the queue entry order, is the current maximum element priority queue
- The minimum priority queue, regardless of the queue order, is the smallest element of the current priority queue
After the code for building the maximum heap is implemented above, there are two basic operations: inserting a node and deleting a node. The inserting node must first be inserted into the last array, and judge whether the inserted value needs to float up to the parent node. Deleting a node is only allowed to delete the value of the root node. After deletion, the last value of the array is placed in the root node, and then adjusted, Sink the value of the completion node. When the above operations are completed, the priority queue is implemented
The implementation code is as follows:
package main
import "fmt"
func main(){
var numArr = []int{2,8,23,4,5,77,65,43}
arrLen := len(numArr)
buildMaxHeapQueue(numArr,arrLen)
var out int
numArr,out = outQueue(numArr)
fmt.Print(numArr,out)
fmt.Print("\n")
numArr = inQueue(numArr,55)
fmt.Print(numArr)
fmt.Print("\n")
numArr,out = outQueue(numArr)
fmt.Print(numArr,out)
fmt.Print("\n")
}
//Queue
func inQueue(arr []int,num int) []int {
arr = append(arr,num)
floatingNode(arr,len(arr)-1)
return arr
}
//Out of queue
func outQueue(arr []int) ([]int,int){
first := arr[0]
arrLen := len(arr)
if arrLen == 0 {
panic("nothing")
}
if arrLen == 1 {
var emptyArr []int
return emptyArr,first
}
//Swap last node and root node values
swapNode(arr,0,arrLen-1)
//Delete the last value of the slice
arr = arr[0:arrLen-1]
//Node subsidence
sinkNode(arr,0,len(arr))
return arr,first
}
//Construction of large top reactor
func buildMaxHeapQueue(arr []int,arrLen int){
for i := arrLen/2;i >= 0; i-- {
sinkNode(arr,i,arrLen)
}
}
//Node value floating judgment
func floatingNode(arr []int,i int){
var root int
if i%2 == 0 {
root = i/2-1
}else {
root = i/2
}
//Judge whether the parent node is smaller than the child node
if arr[root] < arr[i] {
swapNode(arr,root,i)
if i > 1 {
floatingNode(arr,root)
}
}
}
//Tree node value sinking judgment
func sinkNode(arr []int,i int,arrLen int) {
//Left node subscript
left := i*2+1
//Right node subscript
right := i*2+2
largest := i
//If the left node is larger than the parent node, the value is exchanged
if left < arrLen && arr[left] > arr[largest] {
largest = left
}
if right < arrLen && arr[right] > arr[largest] {
largest = right
}
//The node value is greater than the parent node value, and data exchange is required
if largest != i {
//Exchange value
swapNode(arr,i,largest)
//After the exchange is completed, continue to judge whether the exchanged node value needs to continue to sink
sinkNode(arr,largest,arrLen)
}
}
//change of position
func swapNode(arr []int,i,j int) {
arr[i],arr[j] = arr[j],arr[i]
}Heap sort
Heap sort is a sort algorithm designed by using the data structure of heap.
The implementation idea is to build a maximum heap first, and then traverse again. Each traverse exchanges the root node with the value of the last element, and then isolate the last element, because at this time, the last element is the largest element, and then sink the value of the root node to form the maximum heap again, and then repeat the operation to complete the sorting.
package main
import "fmt"
func main(){
var numArr = []int{2,8,23,4,5,77,65,43}
sort := heapSort(numArr)
fmt.Print(sort)
}
//Heap sort
func heapSort(arr []int) []int{
arrLen := len(arr)
//Construction of large top reactor
buildMaxHeap(arr,arrLen)
for i := arrLen-1; i >= 0; i-- {
swap(arr,0,i)
arrLen -= 1
sink(arr,0,arrLen)
}
return arr
}
//Construction of large top reactor
func buildMaxHeap(arr []int,arrLen int){
for i := arrLen/2;i >= 0; i-- {
sink(arr,i,arrLen)
}
}
//Tree node value sinking judgment
func sink(arr []int,i,arrLen int) {
//Left node subscript
left := i*2+1
//Right node subscript
right := i*2+2
largest := i
//If the left node is larger than the parent node, the value is exchanged
if left < arrLen && arr[left] > arr[largest] {
largest = left
}
if right < arrLen && arr[right] > arr[largest] {
largest = right
}
//The node value is greater than the parent node value, and data exchange is required
if largest != i {
//Exchange value
swap(arr,i,largest)
//After the exchange is completed, continue to judge whether the exchanged node value needs to continue to sink
sink(arr,largest,arrLen)
}
}
//change of position
func swap(arr []int,i,j int) {
arr[i],arr[j] = arr[j],arr[i]
}