catalogue

IndexTree

AC automata

IndexTree

Tree array or Binary Indexed Tree (English: Binary Indexed Tree), also named Fenwick tree after its inventor. Its original intention is to solve the calculation problem of Cumulative Frequency in data compression. Now it is mostly used to efficiently calculate the prefix sum, interval sum of sequence. It can get any prefix and in the time of O(logn), and supports the modification of dynamic single point value in the time of O(logn). Spatial complexity O(n)

From Wikipedia

First, let's look at how to get the rightmost 1 in a binary sequence:

Formula n & (~ n + 1) < - > n & (- n)

If you don't understand, you can take a look at my article on bit operation

The typical problem that IndexTree can solve is that there is an array with a length of n. how to efficiently prefix and sum in a certain range, and intelligently solve the problem of how to maintain a structure and fast query after a single point of update: its basic operations mainly include:

1.int sum(int index) find the cumulative sum from 1 to index

2.void add(int index, int d) adds a d to the number at the index position

3.int RangeSum(int index1, int index2) find the cumulative sum from index1 to index2

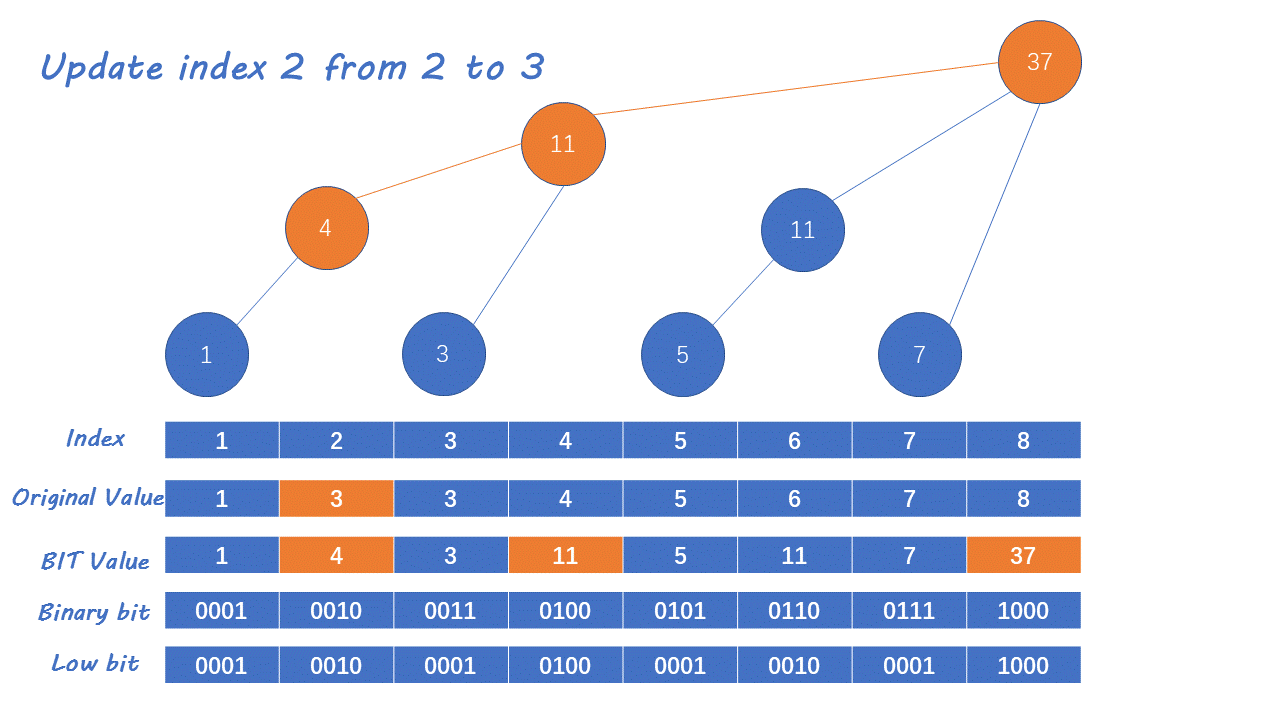
In IndexTree, there is usually a helper array corresponding to i, which manages the cumulative sum of a section of interval for location: for example

Then, suppose there is sequence A = {1, 2, 3, 4, 5, 6, 7, 8}

Note that the 0 position in the help array is not used, starting from the 1 position. As like as two peas, 1 position 1 elements of position, 2 positions look forward, 1 positions have a cumulative sum exactly the same as my length, and 2 positions manage 1~2's cumulative sum. As soon as position 3 looks at the front, there is only no cumulative sum with the same length as him, so position 3 can only manage the number of position 3. As soon as position 4 looks at the front, there is a 3 with the same length as me, so they become partners, and the length becomes 2. As soon as you look forward, there is another one with the length of 1 ~ 2, so they are combined together, so position 4 manages the cumulative sum of positions 1 ~ 8, Similarly, the position of 5, 6, 7 and 8 can also be calculated in the same way, so we get the help number array

 

Corresponding tree structure:

So if I know the small table of the help array, how can I know which range of the original array it manages? Take the comprehensive help array as an example:

 

Suppose we want to know that the position corresponding to position 8 in the help array manages the cumulative sum of that range: first, we only need to write the binary sequence of 8 out of 1000. We eliminate its rightmost 1 and add 1 to this number: that is, 0000 + 1 = 0001. His management range is to eliminate the number of rightmost 1 + 1 to itself, that is, 1 ~ 8 If you don't believe it, we are trying a 6: its corresponding binary sequence is 110. Eliminate the rightmost 1 and add 1 to get 101, that is, 5 to 6

How can we quickly get the accumulation and right from 1 to index in the help array? Similarly, we first write out the binary form of the index, then add the corresponding value of the index position in the help array to the answer, then delete the rightmost 1 in the index array, and then add the corresponding value to the answer in the help array. Repeat the above process until the index becomes 0. Let's take an example. We require the accumulation of 1 ~ 5 and we first write out the binary form of 5: 101. First, we add the value corresponding to position 5 to the answer, then eliminate it. The rightmost 1 becomes 100, that is, 4, and then add the value of position 4 to the answer. Then remove the rightmost 1 and it becomes 0 stop, so we get the cumulative sum of 1 ~ 5 positions

Corresponding code:

	int sum(int index) {
		int ret = 0;
		while (index>0){
			ret += tree[index];
			index -= index & (-index);//Remove the rightmost 1
		}
		return ret;
	}

If a certain number is added to the value of a certain position, it will inevitably cause the values of other positions to change. What about the values of those positions? First of all, your position will certainly change. Other positions can be obtained through calculation. Similarly, first write out its binary sequence, add the rightmost 1 to the original number, and the number is the position that will change. Then repeat the above process until it is greater than n. Add this number to the value of the corresponding position so that we can complete the update.

Corresponding code:

//Index & - index: extract the rightmost 1 of index
	void add(int index, int d){
		while (index <= n) {
			tree[index] += d;
			index += (index & -index);
		}
     }

Corresponding total code:

#pragma once
#include<vector>
#include<queue>
#include<string>
#include<iostream>
using namespace std;

class IndexTree {
	//Note that the subscript starts with 1
	IndexTree(int size)
		:tree(size+1)
		,n(size)
	{}
	int sum(int index) {
		int ret = 0;
		while (index>0){
			ret += tree[index];
			index -= index & (-index);
		}
		return ret;
	}
	//Index & - index: extract the rightmost 1 of index
	void add(int index, int d){
		while (index <= n) {
			tree[index] += d;
			index += (index & -index);
		}
     }
	int RangeSum(int index1, int index2) {//Sum range
		return sum(index2) - sum(index1);
	}
private:
	vector<int>tree;
	int n;
};

The advantage of indexTree over line segment tree is that it is very easy to change indexTree into two-dimensional. The position of the same first row and first column of indexTree in two dimensions is empty and not used, which is similar to that in one dimension. The principle of accumulation in two dimensions is the same as that in one dimension, but there are more columns. Update is the same principle, but there are more columns than one-dimensional.

Corresponding code:

Prefix sum: the sum here is the cumulative sum in the range of coordinates (row, col) to (1, 1)

int sum(int row, int col) {
		int sum = 0;
		for (int i = row + 1; i > 0; i -= i & (-i)) {
			for (int j = col + 1; j > 0; j -= j & (-j)) {
				sum += tree[i][j];
			}
		}
		return sum;
	}

to update:

void update(int row, int col, int val) {
		if (n == 0 || m == 0) {
			return;
		}
		int add = val - nums[row][col];
		nums[row][col] = val;
		for (int i = row + 1; i <= n; i += i & (-i)) {
			for (int j = col + 1; j <= m; j += j & (-j)) {
				tree[i][j] += add;
			}
		}
	}

Given two arbitrary coordinates, find the cumulative sum of the two coordinate ranges:

int sumRegion(int row1, int col1, int row2, int col2) {
		if (n == 0 || m == 0) {
			return 0;
		}
		return sum(row2, col2) + sum(row1 - 1, col1 - 1) - sum(row1 - 1, col2) - sum(row2, col1 - 1);
	}

The old fellow can draw pictures very easily, and it is a very simple geometric relationship.

Corresponding total code:

class IndexTree2D {
public:
	IndexTree2D(const vector<vector<int>>& matrix) {//The constructor assigns a value to it
		tree.resize(matrix.size() + 1, vector<int>(matrix[0].size() + 1));
		nums.resize(matrix.size(), vector<int>(matrix[0].size()));
		n = matrix.size();
		m = matrix[0].size();
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				update(i, j, matrix[i][j]);
			}
		}
	}

	int sum(int row, int col) {
		int sum = 0;
		for (int i = row + 1; i > 0; i -= i & (-i)) {
			for (int j = col + 1; j > 0; j -= j & (-j)) {
				sum += tree[i][j];
			}
		}
		return sum;
	}
	void update(int row, int col, int val) {
		if (n == 0 || m == 0) {
			return;
		}
		int add = val - nums[row][col];
		nums[row][col] = val;
		for (int i = row + 1; i <= n; i += i & (-i)) {
			for (int j = col + 1; j <= m; j += j & (-j)) {
				tree[i][j] += add;
			}
		}
	}

	int sumRegion(int row1, int col1, int row2, int col2) {
		if (n == 0 || m == 0) {
			return 0;
		}
		return sum(row2, col2) + sum(row1 - 1, col1 - 1) - sum(row1 - 1, col2) - sum(row2, col1 - 1);
	}

private:
	vector<vector<int>>tree;
	vector<vector<int>>nums;
	int n;
	int m;
};

AC automata

AC automata mainly solves the problem of finding multiple candidate strings in a large string

The basis of AC automata is Trie tree. Different from the Trie tree, each node in the tree has a pointer (or reference) to the child and a fail pointer, which indicates that the input character is different from all the child nodes of the current node (note that it does not match the node itself), and the state to which the state of the automata should be transferred (or the node to which it should be transferred). The function of the fail pointer can be similar to the function of the next array in the KMP algorithm.

Let's now look at an AC automaton constructed from the target string set {abd,abdk, abchijn, chnit, ijabdf, ijaij}

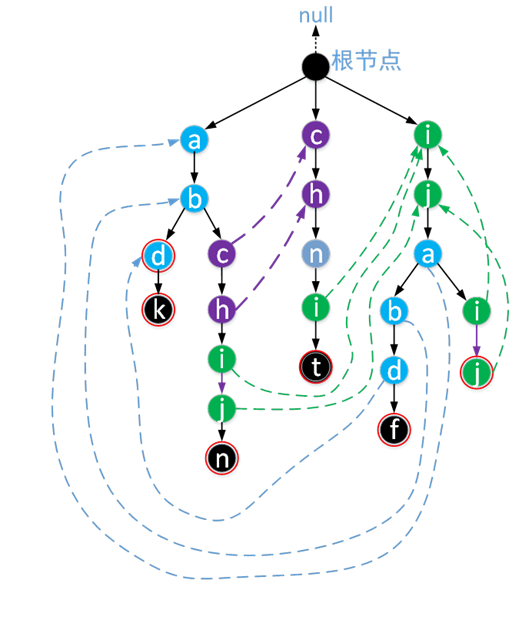
The dotted line represents the direction of the fail pointer.

Note: 1 Each node has a fail pointer, and the root node's fail pointer points to null

           2. The fail pointers of the children in the first layer below the root node all point to the root node

           3. For failure pointers in other locations, first check whether the failure pointer of the parent node has its own path. If so, let the failure pointer of the current location point to the node pointed by the parent failure pointer. If there is no path, continue to go up through the failure pointer. If it is empty, let the failure pointer point to the root node

4. Meaning of fail pointer: if the path formed at the end of the current character must be str, which string prefix and str suffix has the maximum matching length. The fail pointer points to the node position corresponding to that string.

for instance:

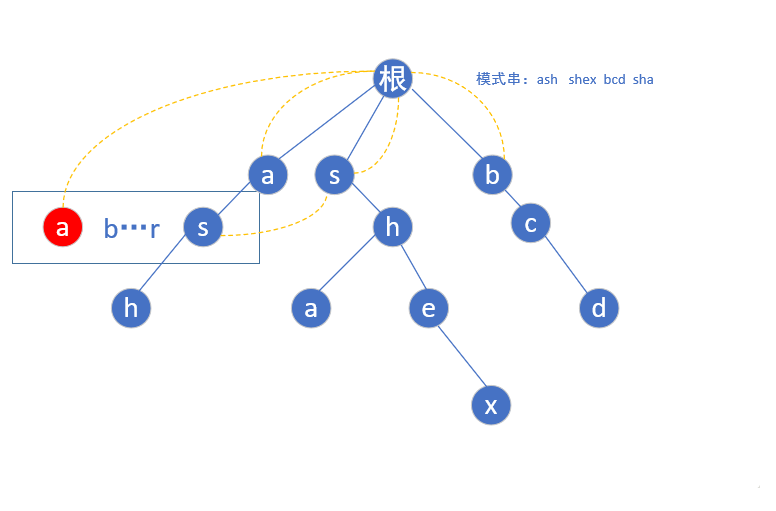
A string asdedf goes to the prefix tree to find out whether there is such a pattern string. First, start from the root node to see whether there is a path to A. if some of the expressions are matching downward and whether there is a path to s, then they directly come to the s node through the fail pointer. Why? This is because the position pointed to by the fail pointer can retain the characters that may match the candidate string, Exclude characters that cannot match the candidate string

How do we collect the matched strings? Each time we come to a position, follow the fail pointer around to see if there is a Hou string. If there is a Hou string, we will collect it, and if there is no, we will continue to match

Corresponding code:

struct Node {
	bool endUse;//Has the answer been added to this string before
	Node* fail;
	vector<Node*>nexts;
	string end;//If end is not empty, it indicates the end of a string
	Node()
		:endUse(false)
		,fail(nullptr)
		,nexts(26)
		,end("")
	{}
};
class ACAutomation {
public:
	ACAutomation()
	{
		_root = new Node;
	}
	void Insert(const string& str) {//Same as prefix tree
		Node* cur = _root;
		int index = 0;
		for (int i = 0; i < str.size(); i++) {
			index = str[i] - 'a';
			if (cur->nexts[index] == nullptr) {
				cur->nexts[index] = new Node;
			}
			cur = cur->nexts[index];
		}
		cur->end = str;
	}

	void build() {
		queue<Node*>q;//Use width first traversal
		q.push(_root);
		Node* cur = nullptr;
		Node* cfail = nullptr;
		while (!q.empty()) {
			cur = q.front();
			q.pop();//The father goes out of the queue to set the child's fail pointer
			for (int i = 0; i < 26; i++) {
				if (cur->nexts[i]) {
					cur->nexts[i]->fail = _root;//First, it points to the root node by default. Later, if it is found, it will be changed again
					cfail = cur->fail;
					while (cfail)//Find the position of the fail pointer to point to
					{
						if (cfail->nexts[i]) {//Found and modified the location
							cur->nexts[i]->fail = cfail->nexts[i];
							break;
					    }
						cfail = cfail->fail;
					}
				}
				q.push(cur->nexts[i]);
			}
		}
	}
	vector<string>containWords(const string& content) {//Collect answers
		Node* cur = _root;
		Node* follow = nullptr;
		vector<string>ans;
		int index = 0;
		for (int i = 0; i < content.size(); i++) {
			index = content[i] - 'a';
			//If the current character is not matched on this road, it will go down the next path in the direction of fail
			while (cur->nexts[index] == nullptr && cur != _root) {
				cur = cur->fail;
			}
			//Now the path can continue to match
			//Now the node is the root node of the prefix tree
			cur = cur->nexts[index] != nullptr ? cur->nexts[index] : _root;
			follow = cur;//Go to any node and follow the fail pointer
			while (follow != _root) {
				if (follow->endUse) {//It has been used to prevent repeated collection
					break;
				}
				if (follow->end != "") {//eureka
					ans.push_back(follow->end);
					follow->endUse = true;
			   }
				follow = follow->fail;
			}
		}
		return ans;
	}
private:
	Node* _root;
};