preface
I just learned it(
Because it has not been deeply studied, it is called "shallow learning and shallow notes".
This short note is mainly based on Luogu P4097 [HEOI2013]Segment This template question is simple, and the title description is brief.
thinking
Starting from a relatively good starting point, in fact, Li Chao line segment tree can be invented by itself to some extent?
First of all, when you see this question, you will find that we need a DS to maintain the "container" of such a line segment, which needs to complete various operations such as the question.
Obviously, we maintain the number of the segment with the largest value in each interval, so we need the segment tree to maintain this thing.
There are two steps to consider how to keep each interval optimal every time a line segment is inserted:
-
This interval is a subset of the definition domain of the line segment, i.e. \ ([L,R] \in D. \)
-
Compare this segment with the optimal segment in the current interval to keep the interval optimal.
The first step is easy to implement, so consider the second, how to compare?
We consider that the influence of adding a line segment is transmitted down through continuous differentiation between the two partitions. The following is a classified discussion:
Suppose that the newly added line / segment is \ (f \), the original maximum value is \ (g \), and the midpoint of the interval is \ (mid. \)
-
\(f) slope greater than \ (g: \)
-
If \ (f (MID) > G (MID) \), then \ (f \) must be optimal in the right sub interval, while \ (g \) may still be better in the left sub interval.
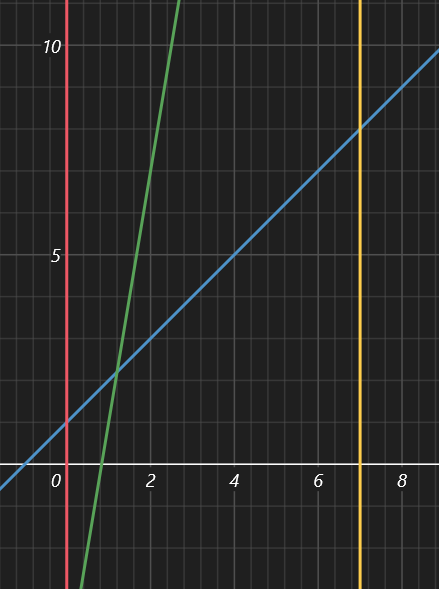
-
On the contrary, \ (g \) must be optimal in the left sub interval, while \ (f \) may still be better in the right sub interval.
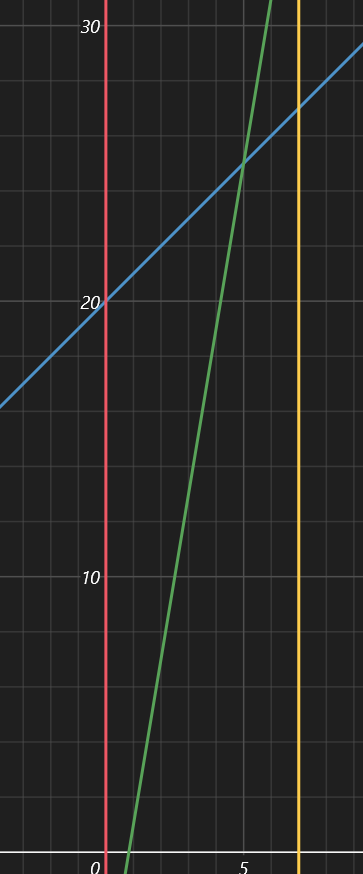
-
-
\(g) slope greater than \ (f: \)
-
If \ (f (MID) < g (MID) \), then \ (f \) must be optimal in the left sub interval, while \ (g \) may still be better in the right sub interval.

-
On the contrary, \ (g \) must be optimal in the right interval, while \ (f \) may still be better in the left sub interval.

-
There are also some special cases, such as straight lines / line segments with the shape of \ (f(x) = d \) (\ (d \) is a constant). We reduce them to each comparison point to facilitate comparison(
Of course, when comparing, we also need to consider the size of the number, so when comparing, we add a little (EPS) to the smaller number to ensure that we get the best choice with smaller number every time.
Then you can code. In terms of complexity, the bottleneck is that the Pushdown is \ (O(\log n) \), so the query and modification operations are \ (O(\log ^2n) \), and the overall complexity is \ (O(n \log ^2n). \)
Code
#include <iostream>
#include <stdio.h>
#include <cmath>
#include <algorithm>
#include <cstring>
#define Heriko return
#define Deltana 0
#define Romanno 1
#define S signed
#define LL long long
#define DB double
#define R register
#define I inline
#define CI const int
#define CL const long long
#define mkp(a,b) make_pair(a,b)
#define mst(a,b) memset(a,b,sizeof(a))
#define ON std::ios::sync_with_stdio(false);cin.tie(0)
#define Files() freopen("RNMTQ.in","r",stdin);freopen("RNMTQ.out","w",stdout)
using namespace std;
template<typename J>
I void fr(J &x) {
short f(1);
x=0;
char c(getchar());
while(c<'0' or c>'9') {
if(c=='-')
f=-1;
c=getchar();
}
while(c>='0' and c<='9') {
x=(x<<3)+(x<<1)+(c^=48);
c=getchar();
}
x*=f;
}
template<typename J>
I void fw(J x,bool k) {
if(x<0)
x=-x,putchar('-');
static short stak[35];
short top(0);
do {
stak[top++]=x%10;
x/=10;
}
while(x);
while(top)
putchar(stak[--top]+'0');
k?puts(""):putchar(' ');
}
template<typename J>
I J Hmax(const J &x,const J &y) {
Heriko x>y?x:y;
}
template<typename J>
I J Hmin(const J &x,const J &y) {
Heriko x<y?x:y;
}
CI MXX(1e5+1),MOD1(39989),MOD2(1e9);
const DB EPS(1e-12);
I void Hmod(int &x,int y,int mod) {
x=(x+y-1>=mod)?x+y-mod:x+y;
}
#define lc(x) (x<<1)
#define rc(x) (x<<1|1)
struct Line {
DB k,b;
int id;
Line(const DB &k=0,const int &x=0,const int &y=0,const int &id=0) : k(k),b(y-x*k),id(id){}
I DB Calc(int x) {
Heriko k*x+b;
}
I bool Empty() {
Heriko !id;
}
}
t[MXX<<2];
I void Hswap(Line &x,Line &y) {
Line z;
z=x,x=y,y=z;
}
I Line Lmx(Line x,Line y,int v) {
Heriko x.Calc(v)>(y.Calc(v)+((x.id>y.id)?EPS:-EPS))?x:y;
}
void Pushdown(int x,int l,int r,Line v) {
int mid((l+r)>>1);
if(t[x].Empty())
t[x]=v;
else {
if(v.Calc(mid)>t[x].Calc(mid)+(v.id>t[x].id?EPS:-EPS))
Hswap(v,t[x]);
if(v.Calc(l)>t[x].Calc(l))
Pushdown(lc(x),l,mid,v);
else if(v.Calc(r)>t[x].Calc(r))
Pushdown(rc(x),mid+1,r,v);
}
}
void Modify(int x,int lx,int rx,Line v,int l=1,int r=MXX) {
if(lx<=l and r<=rx)
Heriko Pushdown(x,l,r,v);
int mid((l+r)>>1);
if(lx<=mid)
Modify(lc(x),lx,rx,v,l,mid);
if(rx>mid)
Modify(rc(x),lx,rx,v,mid+1,r);
}
Line Query(int x,int pos,int l=1,int r=MXX) {
if(l==r)
Heriko t[x];
int mid((l+r)>>1);
if(pos<=mid)
Heriko Lmx(t[x],Query(lc(x),pos,l,mid),pos);
else
Heriko Lmx(t[x],Query(rc(x),pos,mid+1,r),pos);
}
int n,lmd,lstans,cnt;
S main() {
Files();
fr(n);
while(n--) {
int opt;
fr(opt);
if(!opt) {
int x1;
fr(x1),Hmod(x1,lmd,MOD1);
fw((lstans=Query(1,x1).id),1);
lmd=lstans%MOD1;
}
else {
int x1,x2,y1,y2;
Line v;
fr(x1),fr(y1),fr(x2),fr(y2);
Hmod(x1,lmd,MOD1),Hmod(x2,lmd,MOD1);
Hmod(y1,lstans,MOD2),Hmod(y2,lstans,MOD2);
if(x1>x2)
x1^=x2^=x1^=x2,y1^=y2^=y1^=y2;
if(x1==x2)
v.b=Hmax(y1,y2),v.id=++cnt;
else
v=Line(1.0*(y2-y1)/(x2-x1),x1,y1,++cnt);
Modify(1,x1,x2,v);
}
}
Heriko Deltana;
}