Before introducing the algorithm, I will first introduce you to a very useful website. The visualization process inside can help you better understand the data structure and algorithm
VISUALGO.NET: https://visualgo.net/zh.
Visualization process:
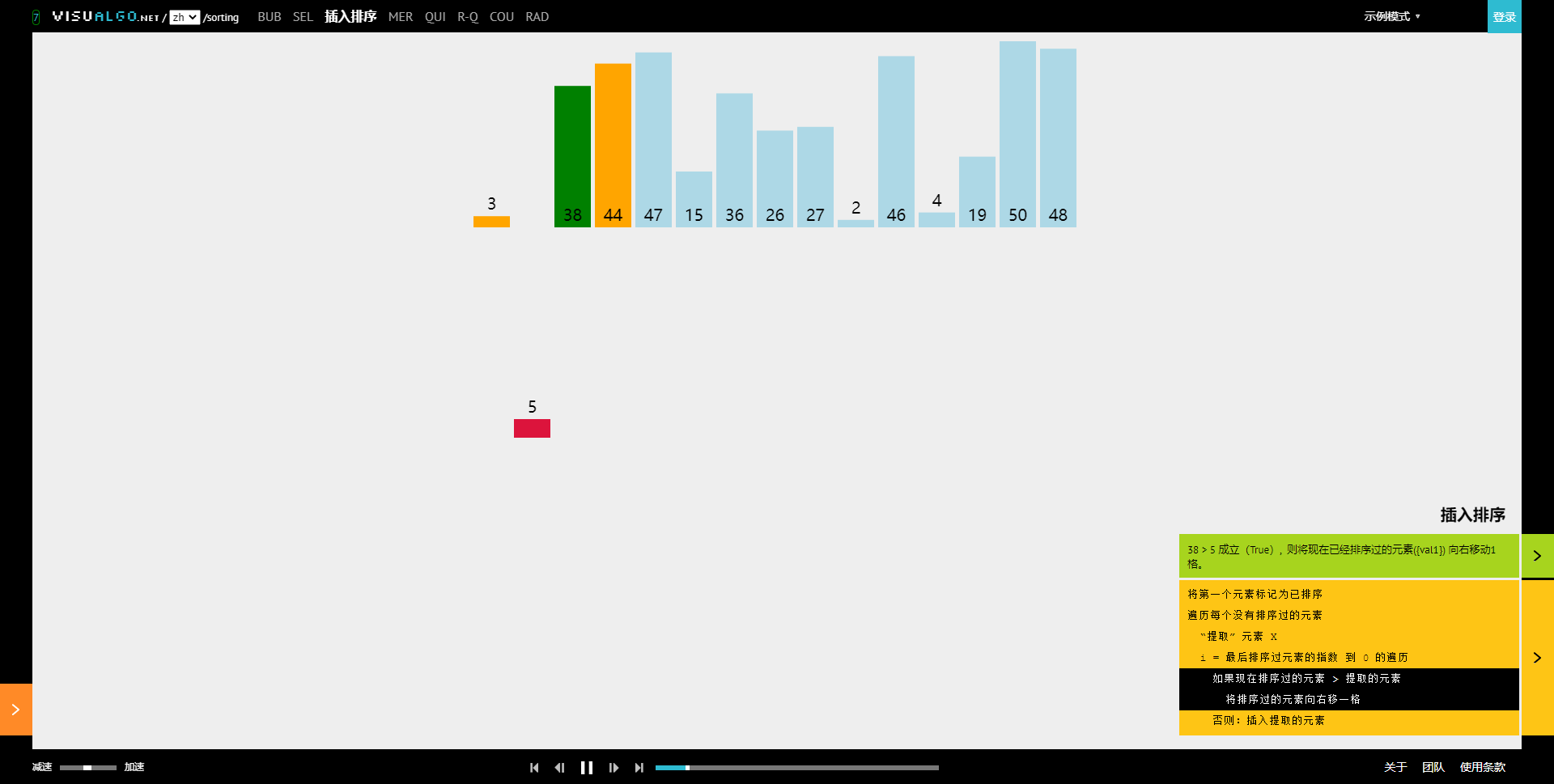
The following contents are explained in three aspects: the idea, characteristics and implementation of the algorithm
1, Direct insert sort
Basic idea: insert one record to be sorted into the previously arranged subsequence according to its keyword size at a time. Similar to playing cards, the order of playing cards in hand.
features:
- It is applicable to sequential storage table and chain storage table;
- It is applied to sort tables with basic order and small amount of data;
- Because only one auxiliary space is used, the space efficiency is O(1);
- In the sorting process, the insertion is executed n-1 times, and each insertion has comparison and move operations. The comparison and move operations depend on the initial state of the table.
- In the best case, the table has been ordered and only compared once without moving, so the time efficiency is O(n)
- In the worst case, the table is in reverse order, the comparison times are (n+2)(n-1)/2, the movement times are (n+4)(n-1)/2, and the time efficiency is O(n^2)
- In the average case, because the elements in the table are random, the best and worst average value is taken, and the time efficiency is O(n^2)
- Each inserted element is compared from back to front, so the relative position of the same element will not change. Therefore, it is a stable sorting method
Implementation: (JAVA)
/**
* Direct insert sort
* It is suitable for sequential storage and linked list storage
*/
public class InsertSortDirect {
int data[] = new int[16];
int size=16;
public static void main(String[] args) {
InsertSortDirect insertsort = new InsertSortDirect();
insertsort.creatData();
insertsort.insert();
}
public void creatData(){
//Randomly generate 16 numbers and store them in the array
for (int i=0;i<size;i++){
int random = (int)(Math.random()*100+1);
data[i] = random;
}
System.out.print("Sequence to be sorted:");
for (int j=0;j<size;j++){
System.out.print(data[j]+" ");
}
}
public void insert(){
int temp = 0;
int j;
for (int i=1;i<size;i++){
if (data[i]<data[i-1]){
temp = data[i];
for (j = i-1;j>=0 && temp<data[j];j--){
data[j+1] = data[j];
}
data[j+1] = temp;
}
}
//Add code to output the sorted sequence
System.out.print("Sorted sequence:");
for (int k=0;k<size;k++){
System.out.print(data[k]+" ");
}
}
InsertSortDirect(){}
}
2, Half insert sort
Halved insertion sequence is an improved algorithm for direct insertion sequence. In the direct insertion sorting algorithm, the sorting process is to compare and move at the same time. The half insertion algorithm separates the comparison from the movement operation. Here is a point to understand, that is, the cleverness of the half insertion algorithm. Let's look at it below:
Here's a sequence sorted in half {1, 2, 3, 5, 8, 10, 36, 25, 20, 80, 40}
At this time, the elements are compared to 25 and 36. At this time, you will find that the sequence before 25 is a small to large sequence. In {1, 2, 3, 5, 8, 10, 36}, use the half search (dichotomy) to find the insertion position of 25, and then insert 25 directly. This process separates the operations of comparison and movement.
Basic idea: find out the position of the element to be inserted by half first; Then uniformly move the elements after the position to be inserted.
features:
- Applies only to sequential storage tables
- Half insertion only reduces the number of comparison elements, about O(nlogn), and the number of comparisons only depends on the number of elements n
- The number of moves has not changed
- Therefore, the time efficiency of the algorithm is O(n^2)
- It is suitable for sorting tables with small amount of data
realization:
/**
* Binary Insertion Sort
* Split half - > FF
* Only for sequential storage
*/
public class InsertSortFf {
int data[] = new int[16];
int size=16;
public static void main(String[] args) {
InsertSortFf ffinsertsort = new InsertSortFf();
ffinsertsort.creatData();
ffinsertsort.insert();
}
public void creatData(){
//Randomly generate 16 numbers and store them in the array
for (int i=0;i<size;i++){
int random = (int)(Math.random()*100+1);
data[i] = random;
}
System.out.print("Sequence to be sorted:");
for (int j=0;j<size;j++){
System.out.print(data[j]+" ");
}
}
public void insert(){
int temp;
int j;
for (int i=1;i<size;i++){
if (data[i]<data[i-1]){
temp = data[i];
//Halve the improvement and add a new piece of code
int low = 0,high = i-1;
int mid;
while (low<=high){
mid = (low+high)/2;
if (data[mid]>temp){
high = mid - 1;
}else{
low = mid + 1;
}
}
for (j = i-1;j>=0 && j>=high+1;j--){
data[j+1] = data[j]; //Unified backward
}
data[high+1] = temp;
}
}
//Add code to output the sorted sequence
System.out.print("Sorted sequence:");
for (int k=0;k<size;k++){
System.out.print(data[k]+" ");
}
}
InsertSortFf(){}
}
3, Hill sort
Hill sort is also an improvement on direct insertion sort. Direct insertion sort is applicable to sort tables with basic order and small amount of data. Hill sort improves these two points. Hill sorting uses the idea of divide and conquer, groups the elements of the sorting table according to the step size, and directly inserts the sorting between each group. After a round, reduce the step size and repeat again until the step size is equal to 1. At this time, the tables are basically ordered, and then the whole sorting table is directly inserted into sorting, so as to improve efficiency.
Basic idea: the records separated by an "increment" form a sub table, and then directly insert and sort each sub table. When the elements in the whole table are basically in an orderly state, directly insert and sort the whole table again.
Feature:
- Applies only to sequential storage tables
- The space efficiency is the same as above: O(1)
- The time complexity of Hill sort depends on the incremental sequence function, but the best incremental function has not been found, so the time complexity is about O(n ^ 1.5). In the worst case, the time complexity is O(n^2)
- Generally, the increment sequence is n/2, which is divided by 2 each time it is reduced
realization:
/**
* Shell Sort
* Group by step and insert directly
* For sequential storage
*/
public class InsertSortShell {
int data[] = new int[16];
int size=16;
public static void main(String[] args) {
InsertSortShell shellinsertsort = new InsertSortShell();
shellinsertsort.creatData();
shellinsertsort.insert();
}
public void creatData(){
//Randomly generate 16 numbers and store them in the array
for (int i=0;i<size;i++){
int random = (int)(Math.random()*100+1);
data[i] = random;
}
System.out.print("Sequence to be sorted:");
for (int j=0;j<size;j++){
System.out.print(data[j]+" ");
}
System.out.println("\n");
}
public void insert(){
int temp;
int i,j,dk;
int k=1; //The purpose is to output the sorting result of each cycle
for (dk=size/2;dk>=1;dk=dk/2){
for (i=dk+1;i<size;i++){
if (data[i]<data[i-dk]){
temp = data[i];
for (j=i-dk;j>=0 && temp<data[j];j-=dk){
data[j+dk] = data[j];
}
data[j+dk] = temp;
}
}
//Output once per cycle
System.out.print("The first"+ (k++) +"Secondary sorting:");
for (int l=0;l<size;l++){
System.out.print(data[l]+" ");
}
System.out.println();
}
}
public InsertSortShell() {}
}
Hill sorting is not easy to understand intuitively. Readers had better think about what hill algorithm has improved, and knock the code manually according to the ideas and characteristics of hill algorithm for in-depth understanding.
Bibliography:
- Big talk data structure
- Royal data structure postgraduate entrance examination guidance
- Graphical data structure - using JAVA
- Algorithm (4th Edition)
If there is any mistake, please correct it