Interesting learning algorithm learning notes
Question 0-1 calculate the number in reverse order
Problem description
This semester Amy began to study an important course - linear algebra. When she learned determinant, she thought it was A very disturbing thing every time she encountered calculating the inverse ordinal number of A given sequence. So she begged her good friend Ray to write A program for her to solve such A problem. In return, she promised to let Ray be her Rumba partner at the weekend ball. The so-called reverse order number of sequence A refers to the number of all binary < I, J > satisfying I < J, A [i] > A [J] in the sequence.
input
The input file contains several test cases. The first line of each case contains only one integer N(1 ≤ n ≤ 500000) representing the number of elements in the sequence. The second line contains n integers separated by spaces, representing n elements in the sequence. The value of each element does not exceed 1 000. N=0 is the end flag of input data.
output
Each case outputs only one line, with only one integer representing the reverse number of a given sequence
sample input
3
1 2 3
2
2 1
0
sample output
0
1
Pseudo code
Open input file inputdata Create output file outputdata from inputdata Read case data from N while N>0 do Create array A[1..N] for i←1 to N do from inputdata Read in A[i] result←GET-THE-INVERSION(A) take result Write as one line outputdata from inputdata Read case data from N close inputdata close outputdata
Among them, line 8 calls the inverse number process of calculation sequence A[1... N]. GET-THE-INVERSION(A) is the key to solve a case, and its pseudo code process is as follows.
GET-THE-INVERSION(A) A[1..N]Represents a sequence N←length[A] count←0 for j←N downto 2 do for i←1 to j-1 do if A[i]>A[j] A reverse order was detected then count←count+1 Accumulate to counter return count
Algorithm 0-1 algorithm pseudo code process of a case to solve the problem of "calculating reverse order number"
cpp
#include <fstream>
#include <iostream>
#include <vector>
using namespace std;
int getTheInversion(vector<int>A)
{
int N = int(A.size());
int count = 0;
for(int j = N - 1;j > 0;j--)
for(int i = 0;i < j;i++)
if(A[i] > A[j])
count++;
return count;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int N = 0;
inputdata >> N;
while(N > 0)
{
vector<int> A(N);
for(int i = 0;i < N;i++)
inputdata >> A[i];
int result = getTheInversion(A);
cout<<result<<endl;
outputdata<<result<<endl;
inputdata>>N;
}
inputdata.close();
outputdata.close();
return 0;
}
Counting problem
Cumulative counting method
In practice, such a problem is often solved through several steps. Each step will produce some data. The goal of the problem is to calculate the sum of the data produced by all steps. For such problems, a counter (variable) is usually set, and then part of the data is added to the counter according to the steps (the operation of each step can often be realized through a cycle), and finally the total data is obtained.
Question 1-1 Knight's gold coins
Problem description
The king rewarded his loyal knights with gold coins. The knight received a gold coin on his first day in office. I got two gold coins every day for the next two days (the second and third days). For the next three days (the fourth, fifth and sixth days), I got three gold coins a day. For the next four days (the seventh, eighth, ninth and tenth days), I got four gold coins every day. This reward form continues all the time: after the knight gets n gold coins every day for N consecutive days, he will get N+1 gold coins every day for N+1 consecutive days, where n is any positive integer. Write a program to calculate the total number of gold coins obtained by the knight for a given number of days (from the first day of service).
Write a program to calculate the total number of gold coins obtained by the knight for a given number of days (from the first day of service).
input
The input file contains at least one line and at most 21 lines. Each line in the input (except the last line) represents a test case, which contains only a positive integer representing days. The value range of days is 1 ~ 10000. The last line of input contains only the integer 0, indicating the end of input.
output
For each test case in the input, exactly one line of data is output. It contains two positive integers separated by spaces. The former represents the number of days in the case, and the latter represents the total number of gold coins obtained by the knight from the first day to the specified number of days.
sample input
10
6
7
11
15
16
100
10000
1000
21
22
0
sample output
10 30
6 14
7 18
11 35
15 55
16 61
100 945
10000 942820
1000 29820
21 91
22 98
Problem solving ideas
(1) Data input and output
According to the description of the input data format of the problem plane, we know that the input file contains multiple test cases, the data of each test case only occupies one line, and only contains a positive integer n representing the number of days of service. N=0 is the input end flag. For each case, the calculated result is the number of gold coins given by the king to the knight, which is output to the file as a line. According to this description, we can use the following process to read data and output data after processing.
Open input file inputdata Create output file outputdata from inputdata Read case data from N while N>0 do result←GOLDEN-COINS(N) take"N result"Write as one line outputdata from inputdata Read case data from N close inputdata close outpudata
Among them, in line 5, the process of calculating the number of gold coins that can be obtained by knights on duty for N days is called golden-codes (N)
The key to a case.
GOLDEN-COINS(N) coins←0, k←1, days←0 while days+k≤N do coins←coins+k*k days←days+k k←k+1 j←N-days coins←coins+k*j return coins
Algorithm 1-1 calculates the total number of gold coins obtained from day 1 to day N for the known days N
cpp
#include <fstream>
#include <iostream>
using namespace std;
int goldCins(int N)
{
int coins = 0,k = 1,days = 0;
while(days + k <=N)
{
coins += k * k;
days += k;
k++;
}
int j = N - days;
coins += k * j;
return coins;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int N;
inputdata >> N;
while(N)
{
int result = goldCins(N);
outputdata<<N<<"."<<result<<endl;
cout<<N<<" "<<result<<endl;
inputdata>>N;
}
inputdata.close();
outputdata.close();
return 0;
}
Question 1-2 Poker Magic
Problem description
How far can you hang a pile of playing cards at the table? If you have a card, you can hang up to half of it at the table. If there are two cards, the top card extends up to half of the lower card, and the bottom card extends up to one-third of the table. Therefore, the total length of two cards hanging on the table is 1 / 2 + 1 / 3 = 5 / 6.. Generally, for N cards, the length of extending out of the desktop is 1 / 2 + 1 / 3 + 1 / 4 +... 1/(n+1), in which the uppermost card extends out of the lower card by 1 / 2, the second card extends out of the lower card by 1 / 3, the third card extends out of the lower card by 1 / 4, and so on, and the last card extends out of the desktop by 1/(n+1). As shown in Figure 1-1.
input
The input contains several test cases, each on one line. Each row of data contains a floating-point number c with two decimal places, which is taken as [0.01, 5.20]. c in the last line is 0.00, indicating the end of the input file
output
For each test case, output the minimum number of cards that can reach the suspension length of c. Output in the format of the output sample.
sample input
1.00
3.71
0.04
5.19
0.00
sample output
3 card(s)
61 card(s)
1 card(s)
273 card(s)
Problem solving ideas
(1) Data input and output
According to the problem description, the format of the input file is similar to that of question 1-1. It contains multiple test cases, each case occupies one line of data, including data representing the total length of playing cards hanging on the table c. c=0.0 is the end flag of input data. The data c of each case is processed, and the calculated result is the number of playing cards with a total length of c that can be hung on the table. The format "number of cards (s)" is output as a line.
Open input file inputdata Create output file outputdata from inputdata Read case data from c while c≠0.0 do result← HANGOVER(c) take"result card(s) "Write as one line outputdata from inputdata Read case data from c close inputdata close outpudata
Among them, line 5 calls the process HANGOVER to calculate the number of playing cards of length c that can be hung at the table © Is the key to solving a case
(2) The algorithmic process of handling a case
HANGOVER(c) n←1, length←0 while length<c do length←length+1/(n+1) n←n+1 if length>c then n←n-1 return n
Algorithm 1-2 the process of calculating the number of cards for the known card suspension length c
In the algorithm, two counters are set in line 1: n (initialized to 1) and length (initialized to 0) represent the number of playing cards and the length hanging at the table, respectively.. The repeated execution condition of the while loop in lines 2 ~ 4 is length < C, 1/(n+1) is accumulated to length each time, and N increases by 1. At the end of the cycle, there must be length ≥ C (equivalently, it means that n is the first card number that makes the condition true). If length > C, it means that n should be reduced by 1 (this is the function of lines 5 to 6).
The running time of the algorithm depends on the number of while loop repetitions n in lines 2 ~ 4. because
1
/
2
+
1
/
3
+
⋯
+
1
/
n
⩽
1
+
1
/
2
+
1
/
3
+
⋯
+
1
/
(
2
⌈
n
/
2
⌉
−
1
)
=
1
+
(
1
/
2
+
1
/
3
)
+
(
1
/
2
2
+
1
/
(
2
2
+
2
)
+
1
/
(
2
2
+
3
)
)
+
⋯
+
(
1
/
2
i
+
1
/
(
2
i
+
1
)
+
⋯
+
1
/
(
2
i
+
2
i
−
1
)
)
+
⋯
+
(
1
/
2
lg
n
/
2
+
1
/
(
2
lg
n
/
2
+
1
)
+
⋯
+
1
/
(
2
lg
n
/
2
⌉
+
2
lg
n
/
2
⌉
−
1
)
)
<
1
+
(
1
/
2
+
1
/
2
)
+
(
1
/
2
2
+
1
/
2
2
+
1
/
2
2
+
1
/
2
2
)
+
⋯
+
(
1
/
2
i
+
1
/
2
i
+
...
+
1
/
2
i
⏟
2
i
)
+
⋯
+
(
1
/
2
lg
[
n
/
2
⌉
+
1
/
2
lg
[
n
/
2
⌉
⏟
2
lg
[
n
/
2
]
+
...
+
1
/
2
lg
[
n
/
2
⌉
)
=
1
+
1
+
...
+
1
⏟
⌈
n
/
2
⌉
=
Θ
(
lg
n
)
\begin{array}{l} 1 / 2+1 / 3+\cdots+1 / n\\ \leqslant 1+1 / 2+1 / 3+\cdots+1 /(2\lceil n / 2\rceil-1)\\ =1+(1 / 2+1 / 3)+\left(1 / 2^{2}+1 /\left(2^{2}+2\right)+1 /\left(2^{2}+3\right)\right)+\cdots\\ +\left(1 / 2^{i}+1 /\left(2^{i}+1\right)+\cdots+1 /\left(2^{i}+2^{i}-1\right)\right)+\cdots\\ \left.+\left(1 / 2^{\lg n / 2}+1 /\left(2^{\lg n / 2}+1\right)+\cdots+1 /\left(2^{\lg n / 2}\right\rceil+2^{\lg n / 2\rceil}-1\right)\right)\\ <1+(1 / 2+1 / 2)+\left(1 / 2^{2}+1 / 2^{2}+1 / 2^{2}+1 / 2^{2}\right)+\cdots\\ +(\underbrace{1 / 2^{i}+1 / 2^{i}+\ldots+1 / 2^{i}}_{2^{i}})+\cdots\\ +(\underbrace{\left.1 / 2^{\lg [n / 2\rceil}+1 / 2^{\lg [n / 2}\right\rceil}_{2^{\lg }[n / 2]}+\ldots+1 / 2^{\lg [n / 2\rceil})\\ =\underbrace{1+1+\ldots+1}_{\lceil\mathrm{n} / 2\rceil}=\Theta(\lg n) \end{array}
1/2+1/3+⋯+1/n⩽1+1/2+1/3+⋯+1/(2⌈n/2⌉−1)=1+(1/2+1/3)+(1/22+1/(22+2)+1/(22+3))+⋯+(1/2i+1/(2i+1)+⋯+1/(2i+2i−1))+⋯+(1/2lgn/2+1/(2lgn/2+1)+⋯+1/(2lgn/2⌉+2lgn/2⌉−1))<1+(1/2+1/2)+(1/22+1/22+1/22+1/22)+⋯+(2i
1/2i+1/2i+...+1/2i)+⋯+(2lg[n/2]
1/2lg[n/2⌉+1/2lg[n/2⌉+...+1/2lg[n/2⌉)=⌈n/2⌉
1+1+...+1=Θ(lgn)
Namely
c
=
Θ
(
l
g
n
)
c=Θ(lgn)
c= Θ (lgn), i.e
n
=
Θ
(
2
c
)
n=Θ(2^c)
n= Θ (2c). So the running time of the algorithm
T
(
c
)
=
n
=
Θ
(
2
c
)
T(c)=n=Θ(2^c)
T(c)=n= Θ (2c). Fortunately, C is between 0.01 and 5.20, otherwise when C is large, the algorithm is very time-consuming.
#include <fstream>
#include <iostream>
using namespace std;
int hangover(double c)
{
int n = 1;
double length = 0.0;
while(length < c)
{
length += 1.0/(n + 1);
n++;
}
if(length > c)
n--;
return n;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
double c;
inputdata >> c;
while(c != 0.0)
{
int result = hangover(c);
outputdata << result <<" card(s)"<<endl;
cout<<result<<" card(s)"<<endl;
inputdata >> c;
}
inputdata.close();
outputdata.close();
return 0;
}
Question 1-3 energy conversion
Problem description
The magician Bai Xiaodu also has problems - now, Bai Xiaodu is in front of an ancient stone gate. There is an ancient magic text on the stone gate. It takes a lot of energy and brain to read and understand this magic text. After a long time, Bai Xiaodu finally understood the meaning of the magic words: there is a stone plate in the stone gate. The magician needs to rotate the stone plate X degrees through magic to make the engraved lines on it correspond to the sky before he can open the stone gate. However, rotating the stone disk requires N energy points, and in order to interpret the ciphertext, there are only M energy points left! It is impossible to destroy the stone gate, because it will require more energy. Fortunately, however, as a magician, a hundred degrees can consume V points of energy, making his energy k times the current remaining energy (you never understand the magician's world, and no one knows how he does it). For example, if a hundred degrees has a point of energy, he can change his energy into (A-V) × Point K (the energy can not be negative at any time, that is, if a is less than V, the conversion cannot be performed). However, in the process of interpreting the ciphertext, baixiaodu advanced his IQ, so he doesn't know whether he can rotate the stone plate and open the stone gate. Can you help him?
input
The first row of the input data is an integer T, indicating that it contains T groups of test cases.
Next, there are T lines of data. Each line has four natural numbers n, m, V and K (see the title description for the meaning of characters).
The data range is as follows:
T ≤ 100 T≤100 T≤100
N , M , V , K ≤ 1 0 8 N, M, V, K ≤ 10^8 N,M,V,K≤108
output
For each test case, please output at least several times of energy conversion before there are enough energy points to open the door; If this is not possible, please output "− 1" directly.
sample input
4
10 3 1 2
10 2 1 2
10 9 7 3
10 10 10000 0
Problem solving ideas
(1) Data input and output
The problem surface tells us that the first line of the input file gives the number of test cases T, and the subsequent t lines of data. Each line represents a case. Read the input data n, m, V and K of each case. After processing, the result is the number of energy conversion times (if the stone gate can be opened after several energy conversion) or − 1 (it is impossible to open the stone gate), and write the result as a line into the output file. The process of representing as pseudo code is as follows.
Open input file inputdata Create output file outputdata from inputdata Number of cases read from Tfor t←1 to T do from inputdata Read case data from N, M, V, K result← ENERGY-CONVERSION(N, M, V, K) take result Write as one line outputdata Medium close inputdata close outpudata
(2) The algorithmic process of handling a case
For a case data N, M, V, K in the problem input, two special cases need to be considered:
1 M ≥ N, i.e. there is enough energy to open the stone gate at the beginning of 100 degrees. At this time, baixiaodu immediately opened the stone gate.
2 m < n and m < V, the energy must be increased to open the stone gate, but according to the problem surface, it is impossible to carry out energy conversion at the beginning. So it's impossible to open the stone gate.
In general, (i.e. M < n and M ≥ V), start from A = M, simulate the repeated conversion of energy A ← (A -V) at A hundred degrees × K set the counter count to track the number of times of energy conversion until the energy is enough to open the stone gate (i.e. A ≥ n), and count is the required value. In this process, the energy conversion A ← (A − V) needs to be monitored × Whether K increases energy A, if A ≥ (A − V) after A certain conversion is detected × K. That means that it is impossible to increase the energy from now on, so in this case, the stone gate can not be opened by A hundred degrees.
Write the above thinking into pseudo code as follows.
ENERGY-CONVERSION(N, M, V, K) A←M, count←0 if A≥N Case 1 then return 0 if A<V Case 2 then return -1; repeat if A≥(A-V)*K Conversion does not increase energy then return -1; A←(A-V)*K; count ← count +1; until A≥N return count
Algorithm 1-3 calculates the minimum number of energy conversions for a case data N, M, V, K
In algorithm 1-3, the time consumption of lines 1 and 12 is constant.. The if structures in lines 2-3 and 4-5 are also constant time operations. In the repeat until structure of lines 6 ~ 11, A starts from m, and the cycle condition is A ≥ n. each time line 9 is repeated, A will increase by at least 1, so it will be repeated at most N-M times. Therefore, the running time of process ENERGY-CONVERSION is O(N-M).
cpp
#include <iostream>
#include <fstream>
using namespace std;
int engergyConversion(int N, int M, int V, int K)
{
int A = M,count = 0;
if(A>=N)
return 0;
if(A<V)
return -1;
do
{
int t = (A - V)*K;
if(A>=t)
return -1;
A=t;
count++;
}while(A<N);
return count;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int T;
inputdata >>T;
for(int t = 0;t<T;t++)
{
int N,M,V,K;
inputdata>>N>>M>>V>>K;
int result=engergyConversion(N, M, V, K);
outputdata<<result<<endl;
cout<<result<<endl;
}
inputdata.close();
outputdata.close();
return 0;
}
Question 1-4 beautiful garden
describe
When Niu Niu Betsy wandered around the barn, she found that farmer John had built a secret greenhouse in which all kinds of exotic flowers and plants were cultivated. Betsy was pleasantly surprised. Her calf's brain was as full of all kinds of ideas as the greenhouse. "I'm going to dig a row of F(7 ≤ f ≤ 10000) flower pits along the farm fence." Betsy thought. "I want to plant one plant in every three pits (every two pits), one Begonia in every seven pits (every six pits), and one daisy in every four pits (every three pits)... And let these flowers bloom forever." Betsy doesn't know how many pits will be left after such planting, but she knows that this number depends on which pit each flower starts from and one plant will be planted in every N pits
Let's help Betsy figure out how many pits will be left to plant other flowers. There are K (1 ≤ K ≤ 100) flowers in total. Each flower starts from the L (1 ≤ L ≤ F) pit and occupies one pit every I-1 pit.. Calculate the remaining unoccupied pits after all planting is completed.
According to Betsy's idea, she can describe the planting plan as follows:
30 [30 pits; 3 different flowers]
1 3 [start from the first pit and plant a rose every three pits]
3.7 [from the third pit, plant one Begonia in every seven pits]
1 4 [start from the first pit and plant a daisy every four pits]
Therefore, the shape of the empty pit in front of the fence in the garden is as follows:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
After planting roses, the shape is as follows:
R . . R . . R . . R . . R . . R . . R . . R . . R . . R . .
After planting Begonia, the shape is as follows:
R . B R . . R . . R . . R . . R B . R . . R . B R . . R . .
After planting daisies, the shapes are as follows:
R . B R D . R . D R . . R . . R B . R . D R . B R . . R D .
Leave 13 pits where no flowers have been planted.
input
Line 1: two integers F and K separated by spaces.
Lines 2~K+1: each line contains two integers Lj and Ij separated by spaces, indicating the position and interval at which a flower is planted.
output
There is only one row and only one integer representing the number of empty pits left after planting.
sample input
30 3
1 3
3 7
1 4
sample output
13
Problem solving ideas
(1) Data input and output
The input to this question contains only one test case. The input starts with two numbers F and K representing the number of pits for planting flowers and the number of flowers. The case also includes two sequences: the planting starting position L[1... K] of each flower and the planting interval I[1... K]. Read these data, process and calculate how many of the f pits are empty after planting all k flowers, and write the results into the output file as a line of data.
Open input file inputdata Create output file outputdata from inputdata Number of cases read from F,K Create array L[1..K],I[1..K] for i←1 to K do from inputdata Read case data from L[i], I[i] result← THE-FLOWER-GARDEN(F, K, L, I) take result Write as one line outputdata in close inputdata close outpudata
Among them, the procedure the-flow-garden (F, K, l, I) is called in line 7 to calculate the number of empty pits left after Betsy has cut K flowers in front of the fence as planned, which is the key to solving this case.
(2) The algorithmic process of handling this case
For a test case, set the number of the pit with the smallest planting position in the K flowers as i, set an empty pit counter count and initialize it to i-1, because the pit before i will not carry any flowers. Start from the current position and check whether a flower will be planted in each pit in turn. If K flowers do not occupy this pit as planned, the count will increase by 1. After all the positions are inspected, the data accumulated in count is the required value.
THE-FLOWER-GARDEN(F, K, L, I) i←MIN-ELEMENT(L) The first pit to plant flowers count←i-1 Of course the previous pit was empty while i≤F Inspect each subsequent pit one by one do for j←1 to K Examine each flower one by one do if i-1 Mod I[j]≡L[j] View page i Is the second pit planted j grow flowers then break this loop if j>K if i No flowers were planted in pit No then count←count+1 Empty pit counter increase i ←i+1 return count
Algorithm 1-4 calculates the number of remaining empty pits for a case data F, K, L, I
cpp
#include <fstream>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int theFlowerGarden(int F,int K,vector<int>L,vector<int>I)
{
int i=*(min_element(L.begin(),L.end()));
int count = i;
while(i<F)
{
int j;
for(j = 0;j < K;j++)
{
if(i % I[j] == L[j])
break;
}
if(j>=K)
count;
i++;
}
return count;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int F, K;
inputdata>>F>>K;
vector<int> L, I;
for(int j = 0;j<K;j++)
{
int lj, ij;
inputdata>>lj>>ij;
L.push_back(lj-1);
I.push_back(ij);
}
int result=theFlowerGarden(F, K, L, I);
outputdata<<result<<endl;
cout<<result<<endl;
inputdata.close();
outputdata.close();
return 0;
}
Simple mathematical calculation
Question 1-5 small degree Brush Gift
Problem description
The annual Baidu star competition began again, and the number of participants set a Guinness world record. Therefore, baidu star decided to reward some people: all contestants whose ID ends with x will receive a beautiful gift
Xiaodu wanted to get this gift very much, so he submitted it many times in a row, and the submitted ID was from a to b. He wants to know how many gifts he can get. Can you help him?
input
A positive integer t in the first line indicates the number of test cases. Next, in line T, there are three integers $x,a,b(0 ≤ x ≤ 10 {18}, 1 ≤ a ≤ b ≤ 10 {18}) $.
output
Line T. The number of gifts obtained by small degree under the data corresponding to each behavior.
sample input
2
88888 88888 88888
36 237 893
sample output
1
6
Problem solving ideas
(1) Data input and output
The problem surface tells us that the first data of the input file indicates the number of test cases T contained. The input data of each case only occupies one line, including three integers representing the mantissa X of ID and the lower bound a and upper bound b of ID value respectively. The calculated result is the number of gift IDS (mantissa x) that can be obtained in a~b, which is output to the file as a line. Expressed as pseudo code as follows.
Open input file inputdata Create output file outputdata from inputdata Number of cases read from T for t←1 to T do from inputdata Read case data from x, a, b result← GIFT(x, a, b) take result Write as one line outputdata in close inputdata close outpudata
Among them, the key to solving a case is to call the process GIFT (x, a, b) in line 6 to calculate the number of gifts that can be obtained.
(2) The algorithmic process of handling a case
For a test case x, a and B, it is easy to think of using enumeration to exhaust all integers of a~b and detect whether the mantissa of each is equal to X. Number of trace equivalents:
GIFT (x, a, b) t← x Decimal digits of m←10^t count ←0 for i ←a to b do if i Mod m=x then count ←count+1 return count
Algorithm 1-5 the algorithm process of accumulating and calculating the number of gifts for a test case data x, a and B
Lines 1 and 2 in algorithm 1-5 calculate m=10^t, where t is the decimal digit of x, which can be realized by the following operations:
m←1while m<x do m←m*10
Obviously, the time is l o g 10 x log_{10}x log10 × x, if there are n numbers between a and B, the running time of lines 3 ~ 6 in the above algorithm is Θ ( n ) Θ(n) Θ (n) Therefore, the running time of algorithms 1-5 is Θ ( l o g 10 x ) + Θ ( n ) Θ(log10x)+ Θ(n) Θ (log10x)+ Θ (n). With the help of mathematical calculation, we can reduce the algorithm time to Θ ( l o g 10 x ) Θ(log_{10}x) Θ(log10x).
GET-GIFT(x, a, b) t← x Decimal digits of m←10t ar ←a Mod m,aq←a/m br ←b Mod m,bq←b/m if ar>x then aq←aq+1 if br<x then bq←bq-1 return b q-aq+1
Algorithm 1-6 the algorithm process of directly calculating the number of gifts for a test case data x, a and B
cpp
#include <iostream>
#include <fstream>
using namespace std;
int getGift(int x,int a,int b)
{
int m = 1;
while(m < x)
m *= 10;
int ar = a % m, aq = a / m;
int br = b % m, bq = b / m;
if(ar > x)
aq++;
if(br < x)
bq--;
return bq - aq + 1;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int t;
inputdata>>t;
for(int i = 0; i < t;i++)
{
int x,a,b;
inputdata>>x>>a>>b;
int result = getGift(x,a,b);
outputdata<<result<<endl;
cout<<result<<endl;
}
inputdata.close();
outputdata.close();
return 0;
}
Question 1-6 find Niu Niu
Problem description
Farmer John keeps a herd of cows. Some Niuniu are very capricious and often run away from home. One day, John learned that one of his wandering cows came out and wanted to take her home immediately. John starts from point N (0 ≤ N ≤ 100000) on the number axis, and Niu Niu haunts point K (0 ≤ K ≤ 100000) on the same number axis. John has two ways of moving: walking or long-distance flying.
Walk: John can walk from point x to point X-1 or point X+1 in one minute
Long distance leap: John can leap from any point X to point 2 X in one minute
Assuming Niu Niu knows nothing about her danger and walks around in place all the time, how long will it take John to catch her at least?
input
The first line of the input file contains only an integer t representing the number of test cases. Followed by T lines of data, each line of data describes a test case, including two integers separated by spaces: N and K.
output
There is only one line of output for each case: the minimum time (minutes) for John to catch Niuniu.
sample input
2
5 17
3 21
sample output
4
6
Problem solving ideas
(1) Data input and output
According to the format description of input and output data in the problem plane, we can express the process of processing all cases as follows.
Open input file inputdata Create output file outputdata from inputdata Number of cases read from T for t←1 to T do from inputdata Read case data from N, K result←CATCH-THAT-COW(N, K) take result Write as one line outputdata in close inputdata close outpudata
CATCH-THAT-COW(N, K)
if N≥K
then return N-K
p←max{i|2i≤K}, q←max{i|2iN≤K}, t←max{i|2i≤N}
if N2q=K
then return q
a← q+K-N2q , b← q+1+ N2q+1-K, c←(N-2t)+(p-t)+(K-2p)
d←(N-2t)+(p-t+1)+(2p+1-K), e←(2 t+1 -N)+(p-t+1)+(K-2 p ), f ←(2t+1-N)+(p-t)+(2p+1 -K)
return min{a, b, c, d, e, f}
cpp
#include <fstream>
#include <iostream>
using namespace std;
pair<int, int> calculate(int x, int base = 1)
{
int t = 0, p = base;
while (p < x)
{
t++;
p *= 2;
}
if (p > x)
{
t--;
p /= 2;
}
return pair<int, int>(t, p);
}
int catchTheCow(int N, int K)
{
if (N >= K)
{
return N - K;
}
pair<int, int> x = calculate(K, N);
int q = x.first, n2q = x.second;
if (n2q == K)
{
return q;
}
x = calculate(K);
int p = x.first, one2p = x.second;
x = calculate(N);
int t = x.first, one2t = x.second;
int a = q + K - n2q, b = q + 1 + 2 * n2q - K, c = (N - one2t) + (p - t) + (K - one2p);
int d = (N - one2t) + (p - t + 1) + (2 * one2p - K), e = (2 * one2t - N) + (p - t + 1) + (K - one2p), f = (2 * one2t - N) + (p - t) + (2 * one2p - K);
return min(a, min(b, min(c, min(d, min(e, f)))));
}
int main()
{
ifstream inputdata("Catch The Cow/inputdata.txt");
ofstream outputdata("Catch The Cow/outputdata.txt");
int T;
inputdata >> T;
for (int t = 0; t < T; t++)
{
int N, K;
inputdata >> N >> K;
int result = catchTheCow(N, K);
outputdata << result << endl;
cout << result << endl;
}
inputdata.close();
outputdata.close();
return 0;
}
Problems 1-7 poor bus scheduling
describe
You are a grumpy man and hate waiting. You're going to visit a friend in New Orleans. When you come to the bus stop, you find that the schedule here is the worst in the world. The station does not list the arrival and departure schedule of each bus, only the departure interval of each adjacent bus
Grumpy, you grab your tablet out of your bag and try to write a program to calculate how long the nearest bus needs to wait. Hey, that's all you can do, isn't it?
input
The input to this question contains no more than 100 test cases. The input data format for each case is as follows.
The data of a test case includes four parts:
First line - there is only one line, "START N", where N represents the number of bus routes (1 ≤ N ≤ 20).
Route departure interval interval line - there are N lines in total. Each line is composed of M(1 ≤ m ≤ 10) departure intervals. These data represent the interval length from the last departure of each bus on this route to the departure time of this bus. The duration of each interval is an integer between 1 and 1000
Arrival time - one line only. This line of data represents the time you wait when you arrive at the station. This data represents the number of time units from the start of the station to your arrival at the station on the same day (all trains on all lines start from time 0). This is a nonnegative integer (if it is 0, it means that the bus starts when you arrive at the station) ending line - a single line, "END". After the last test case, there is a line "ENDOFINPUT" as the input END flag
output
For each test case, there is exactly one line of output. This line contains only one unit of time that you need to wait before the next bus arrives. We hope the bus you are waiting for is for New Orleans!
be careful
Each bus runs continuously on its route. If the passenger arrives at the departure time of the bus, he / she will get on the bus.
sample input
START 3
100 200 300
400 500 600
700 800 900
1000
END
START 3
100 200 300 4 3 2 4 2 22
800
10 1000
32767
END
ENDOFINPUT
sample output
200
20
The pseudo code is described as follows
Open input file inputdata
Create output file outputdata
from inputdata Read a line from to s
while s≠"ENDOFINPUT"
do Skip s Medium"START",And read N
Create array durations[1..N]
for i←1 to N
do from inputdata Read a line from to s
take s Each integer data in is added to the durations[i]in
from inputdata Read in arrival
result←WORLD-WORST-BUS-SCHEDULE(durations, arrival)
take result Write as one line outputdata
stay inputdata Skip a line"END"
from inputdata Read a line from to s
close inputdata
close outpudata
Among them, the key to solving a case is to call the process world-world-bus-schedule (durations, arrival) in line 11 to calculate the minimum waiting time of passengers.
(2) The algorithmic process of handling a case
For a case, record the departure interval duration of each train in a group of array durations, d u r a t i o n s [ i ] [ l ] durations[i][l] durations[i][l] refers to the time interval between the j-th departure of train I and the j-1 st departure. T i = ∑ j = 1 m d u r a t i o n s [ i ] [ l ] T_i=\sum^m_{j=1}durations[i][l] Ti = ∑ j=1m duration [i] [l] represents the time taken for each bus on route I to run a cycle (i=1, 2,..., n). If the arrival time of passengers in this case is assumed to be arrival, $Ri=arrival \mod Ti $indicates the time in the latest operation cycle after the I train has completed several cycles when the passengers arrive at the station. For example, in case 1 in the input example, one operation cycle T1 of No. 1 bus and No. 3 bus is 100 + 200 + 300 = 600, and the arrival time of passengers a r r i v a l = 1000 , R 1 = a r r i v a l m o d T 1 = 1000 m o d 600 ≡ 400 arrival=1000, R1=arrival \mod T1=1000 \mod 600≡400 arrival=1000,R1=arrivalmodT1=1000mod600≡400. This means that the third bus of No. 1 bus has been running for a cycle, and the passengers arrive at the station at 400 hours. Therefore, passengers should wait for the bus with a departure time of more than 400 from the beginning to the latest in the current cycle. The waiting time is naturally from the first to make the difference T i = ∑ j = 1 m d u r a t i o n s [ i ] [ l ] − R i ≥ 0 ( 1 ≤ k ≤ m i ) T_i=\sum^m_{j=1}durations[i][l]-R_i\ge 0(1 \le k \le m_i) Ti = ∑ j=1m − duration [i] [l] − Ri ≥ 0 (1 ≤ k ≤ mi). In this example, the value is (100 + 200 + 300) − 400 = 600 - 400 = 200. The minimum waiting time of all n channels is the required value. The above algorithm idea is written into pseudo code, and the process is as follows.
WORLD-WORST-BUS-SCHEDULE(durations, arrival)

Suppose there is No. n bus in the case, and the number of classes with the largest number of shifts is m. The running time of the algorithm depends on the repetition times of the two-level nested loop in lines 2 ~ 9. The outer for loop is repeated N times, and the fourth line of the inner layer is actually a loop (calculating the cumulative sum), and the maximum number of repetitions is m. Similarly, the while loop on lines 7 to 8 is repeated at most m times. The cycles of the two inner layers are parallel, so the running time is O(nm).
#include <fstream>
#include <iostream>
#include <vector>
#include <string>
#include <sstream>
using namespace std;
int sum(vector<int> &a,int start,int end)
{
int s = 0;
for(int i = start;i <= end;i++)
{
s += a[i];
}
return s;
}
int WorldsWorstBusSchedule(vector<vector<int>> duration,int arrival)
{
int N = int(durations.size());
vector<int> time(N);
for(int i = 0;i < N;i++)
{
int mi = int(durations[i].size());
int Ti = sum(durations[i],0,mi - 1);
int Ri = arrival % Ti;
int k = 0,sigm = 0;
while(sigm - Ri < 0)
sigm += durations[i][k++];
time[i] = sum(durations[i],0,k - 1) - Ri;
}
return *min(time.begin(),time.end());
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
string s;
getline(inputdata,s);
while(s != "ENDOFINPUT")
{
istringstream strstream(s);
string str;
strstream >> str; //Skip START
int N;
strstream N;
vector<vector<int>> durations(N);
for(int i = 0;i < N; i++)
{
getline(inputdata,s);
strstream = istringstream(s);
int x;
while(strstream >> x)
{
durations[i].push_back(x);
}
}
int arrival;
inputdata>>arrival;
int result = WorldsWorstBusSchedule(durations,arrival);
outputdata<<result<<endl;
cout<<result<<endl;
getline(inputdata,str);//Break line
getline(inputdata,str);//Skip END
getline(inputdata,s);//Read the first line of the new case
}
}
Question 1-8 bubble sorting
Problem description
Bubble sorting is a simple sorting algorithm. The algorithm repeatedly scans the list to be sorted and compares the adjacent element pairs. If the order of the two is wrong, they will be exchanged. In this way, the list is scanned repeatedly until there are no elements to be exchanged in the list, which means that the list has been sorted. The reason why the algorithm is called this name is that the smallest element appears at the top of the list like a "bubble", which is a sort algorithm based on comparison.
Bubble sorting is a very simple sorting algorithm, and its running time is O(n2). Each operation starts from the beginning of the list to compare adjacent items, and exchange the two when necessary. Repeat this operation several times until no more switching operation is required. Assuming that the sequence is arranged in ascending order after just T times of operation, we say that T is the number of bubble sorting times of the sequence. Here is an example. The sequence is "5 1 4 2 8", and the bubbling order is as follows.
First operation:
(5 1 4 2 8) − > (1 5 4 2 8), compare the first two elements and exchange them.
(1 5 4 2 8) − > (1 4 5 2 8), swap because 5 > 4.
(1 4 5 2 8) − > (1 4 2 5 8), swap because 5 > 2.
(1 4 2 5 8) − > (1 4 2 5 8) since these two elements have maintained order (8 > 5)
, the algorithm does not exchange them.
Second operation:
( 1 4 2 5 8 ) −> ( 1 4 2 5 8 )
(1 4 2 5 8) − > (1 2 4 5 8), swap because 4 > 2.
( 1 2 4 5 8 ) −> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) −> ( 1 2 4 5 8 )
After T = 2 times, the sequence has been sorted, so we say that the number of bubble sorting times of this sequence is 2. ZX learned bubble sorting in algorithm class, and his teacher left him an assignment. The teacher gave ZX an array A with N unequal elements, which has been arranged in ascending order. The teacher told ZX that the array was obtained after K times of bubble sorting. The question is: how many initial states does A have that make it bubble sort, and the number of times is just K? The result may be A large value. You only need to output the remainder of the number relative to the modulus 20100713
input
The input contains several test cases.
The first line contains an integer t representing the number of cases (t ≤ 100 000).
Followed by the T line, which represents the data of each case.
Each row contains two integers N and K(1 ≤ N ≤ 1000000, 0 ≤ K ≤ N − 1), where N represents the length of the sequence and K represents the number of times to bubble sort the sequence.
output
For each case, the initial case of the output sequence is the remainder of the analog-to-digital 20100713, one line for each.
sample input
3
3 0
3 1
3 2
sample output
1
3
2
#include <fstream>
#include <iostream>
#include <vector>
using namespace std;
void bublleSortRounds(int N,int K,int k,vector<int> &x,int &count)
{
if(k >= K)
{
int item = 1;
for(int i = 0;i < K; i++)
item = (item * x[i]) % 20100713;
count = (count + item) % 20100713;
return;
}
int begin,end;
if(k == 0){ begin = N - 1; end = K; }
else{ begin = x[k - 1] - 1; end = K - k;}
for(int p = begin; p >= end; p==)
{
x[k] = p;
bublleSortRounds(N, K, k + 1, x, count);
}
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int T,N,K;
inputdata >> T;
for(int t = 0; t < T; t++)
{
inputdata>>N>>K;
int count = 0;
vector<int> x = vector<int>(K);
bublleSortRounds(N, K, 0, x, count);
outputdata<<count<<endl;
cout<<count<<endl;
}
inputdata.close();
outputdata.close();
return 0;
}
Properties of Graphs
There is a certain relationship between the things involved in some counting problems. Such problems can often be expressed as a graph: each thing in the problem is regarded as a vertex. If there is such a relationship between the two vertices, an arc called an edge is made between the two vertices. The formal description is a set composed of things in the problem, which is recorded as vertex set V={v1,v2,..., vn}, edge set E={(vi, vj)| vi, vj ∈ V, and vi and vj have a relationship}.
For example, figure 1-3 shows the friend relationship among five people, Edward, John, Philips, Robin and Smith. Among them, Edward is friends with Robin and Smith, John is friends with Philips and Robin, Philips is friends with John, Robin and Smith, Smith is friends with Edward, Philips and Robin, and Robin is friends with everyone else.
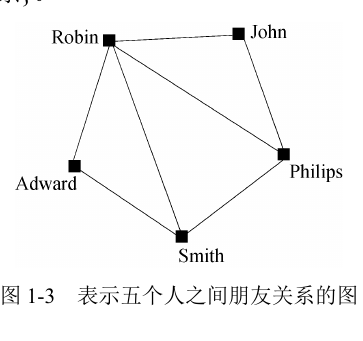
Figure G is marked as < V, E >. Mathematicians have studied graphs for a hundred years. There are many useful properties that can help us easily solve the counting problem. For example, there is a famous "handshake" theorem in graph theory.
Definition 1-1
Let g = < v, E > be an undirected graph, v ∈ v, and call v as the degree of the edge. The sum of the number of endpoints is v, which is called degree for short, and is recorded as d(v).
We have the following conclusions about the degrees of all vertices in the graph.
Theorem 1-1 (handshake theorem)
Let g = < V, E > be any undirected graph, V={v1,v2,..., vn},|E|=m, then
∑
i
=
1
n
=
2
m
\sum^n_{i=1} = 2m
i=1∑n=2m
That is, the sum of the degrees of all vertices is twice the number of edges
It is proved that each edge (including ring) in G has two endpoints, so when calculating the sum of the degrees of each vertex in G, each edge provides 2 degrees. Of course, m edges provide 2m degrees in total.
The handshake theorem shows that the sum of the degrees of each vertex in the graph must be even
Question 1-9 Party Games
Problem description
Baidu star finals is not only a competition for a group of programming giants, but also a rare get-together for many netizens in the circle. In the week-long party, there are always a variety of interesting games.
One year at the finals party, an interesting game was as follows:
The game is hosted by Robin, with A total of N participants (including the host). Robin asks everyone to tell the number of people they know on the scene (if A knows B, B also knows A by default). After receiving the data reported by all players, he will judge whether someone is lying. Robin said that if he can judge correctly, he hopes that every player can work in Baidu after graduation.
In order to help Robin keep these talents, please give him some advice now.
Special note:
1. Everyone knows Robin.
2. People you know don't include yourself.
input
The input data includes multiple groups of test cases, and each group of test cases has two lines. First, one line is an integer n (1 < n ≤ 100), indicating all the people participating in the game, and the next line includes N-1 integers, indicating the number of people reported by other people except the host.
Input ends when N is 0.
output
Please help host Robin to make a judgment according to the input data of each group: if it is determined that someone is lying, please output "Lieabsolutely"; Otherwise, output "may truth".
The output of each group of data occupies one row
sample input
7
5 4 2 3 2 5
7
3 4 2 2 2 3
0
sample output
Lie absolutely
Maybe truth
Problem solving ideas
(1) Data input and output
According to the description of the input file format in the question plane, there are several test cases in the file. The data of each case starts with the integer n representing the number of people, and then N-1 integers represent the number of acquaintances reported by everyone except the host. Judge whether someone lies in the case, and output a line of "may truth" or "lie alone" according to the calculation results. N=0 is the end of input flag.
Open input file inputdata Create output file outputdatawhile N≠0 do Create array a[1..N] for i←1 to N-1 do from inputdata Read in a[i]a[N] ←N-1 Robin Know everyone result← PARTY-GAME(a)if result=true then take"Maybe truth"Write as one line outputdata else take"Lie absolutely"Write as one line outputdata from inputdata Read case data from N close inputdata close outpudata
Among them, the key to solve a case is to call the process PARTY-GAME(a) in line 9 to judge whether someone in N individuals is lying.
(2) The algorithmic process of handling a case
In one case, two people know each other as a relational undirected graph G = < V, E >. The cognitive relationship between n individuals can be expressed as an undirected graph G = < V, E >. The elements in the edge set E represent two people, and the vertex set V={v1,v2,..., vn} represents the cognitive relationship between these n people. Using the handshake theorem, we add the number of people who know each case (including n − 1 reported by the host) to investigate the parity of the sum. If it is an odd number, someone must lie. Equivalently, set a counter count (initially 0) to detect the number of acquaintances reported by each person (including the host). If it is an odd number, the count will increase by 1, and judge according to the parity of the count. The pseudo code process is represented as follows:
PARTY-GAME(a)n←length[a]count←0for i←1 to n Z Check the number of acquaintances reported by each person do if a[i] is odd then count←count+1return count is even
Algorithm 1-11
The process of judging whether there are guests lying at the party by using the handshake theorem
For a case, if there are n people at the party, including the host, the for loop on lines 3 to 5 will be repeated N times. So the running time of the algorithm for a case is Θ (n).
#include <iostream>
#include <fstream>
#include <vector>
using namespace std;
bool partyGame(vector<int> a)
{
int n = int(a.size());
int count = 0;
for (int i = 0; i < n; i++)
if (a[i] % 2)
count++;
return (count % 2) == 0;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int n;
inputdata >> n;
while (n)
{
vector<int>a(n);
a[n - 1] = n - 1;
for (int i = 0; i < n - 1; i++)
inputdata >> a[i];
if (partyGame(a))
{
outputdata << "Maybe truth" << endl;
cout << "Maybe truth" << endl;
}
else
{
outputdata << "Lie absolutely" << endl;
cout << "Lie absolutely" << endl;
}
inputdata>>n;
}
inputdata.close();
outputdata.close();
return 0;
}
Replacement and rotation
There is a set a composed of N pairwise unequal elements a1, a2,..., an, considering a 1-1 transformation of a itself σ: a’ 1= σ (a1), a’2= σ (a2),…,a’n= σ (an). In other words, a'1,a'2,..., a'n is a rearrangement of a1, a2,..., an. In mathematics, it is called such a correspondence σ Is a permutation of A.
[example 1] set A = {2,4,3,1}, σ (2)=1 , σ (4)=2, σ (3)=3, σ (1) = 4 is A permutation on A.
set up σ Is a substitution of A={a1, a2,..., an}: A2= σ (a1), a3= σ (a2),…, an= σ (an − 1), then σ For a rotation on a.
[example 2] in example 1, due to σ (2)=1, σ (1)=4, σ (4) = 2, so σ It can be regarded as a rotation on the subset A1={2,1,4} of A σ 1.
[example 3] identity transformation on single element set A={a} σ (a)=a is considered rotation.
There are the following important propositions between replacement and rotation
Theorem 1-2
Any permutation on set A={a1, a2,..., an} σ, It can be uniquely 5 decomposed into the rotation on several disjoint subsets of a, and the union of these subsets is a
[example 4] in example 1, A={2,4,3,1} is replaced σ It can be decomposed into A1 in example 2 σ 1: Identity transformation on 2 → 1, 1 → 4, 4 → 2 and A2={3} σ 2: 3 → 3, and A= A1 A2,A1 A2 = ∅.
Question 1-10 Niu Niu queuing
Farmer John has N (1 ≤ N ≤ 10000) cows. At night, they have to milk in a row. Each Niuniu has a unique index with a value of 1 ~ 100000 indicating the degree of her temper. John wants to rearrange the angry cows in ascending order of the angry index (from small to large) because the angry cows are more likely to damage John's milking equipment. In this process, the positions of two Niuniu (not adjacent) may be exchanged, and it takes X+Y time units to exchange the positions of two Niuniu whose temper index is X and Y.
Please help John calculate the shortest time required to rearrange Niuniu.
input
The input file contains several test case data. Each test case consists of two lines of data:
The first line is an integer N representing the number of Niuniu.
The second line contains N integers separated by spaces, representing the temper index of each Niuniu.
N=0 is the end flag of input data. There is no need to deal with this case.
output
For each test case, the output line contains an integer representing the minimum time required to rearrange cattle and girls in ascending order of temper index.
sample input
3 2 3 1 6 4 3 1 5 2 6 0
sample output
7
18
Problem solving ideas
(1) Data input and output
The problem input file contains several test cases, and the input data of each case has two lines: the first line contains an integer n representing the number of Niuniu, and the second line contains n integers representing the temper index of Niuniu. N=0 is the end flag of input data. Niu Niu's temper index in the case can be organized into an array, which calculates the minimum cost of rearranging Niu Niu in ascending order of temper index. Write the calculated result to the output file as 1 line
Open input file inputdata Create output file outputdata from inputdata Number of people read in N while N≠0 do Create array a[1..N] for i←1 to N do from inputdata Read in a[i] result←COW-SORTING(a) take result Write as one line outputdata from inputdata Read case data from N close inputdata close outpudata
Among them, the key to solving a case is to call the procedure COW-SORTING(a) in line 8 to calculate the minimum cost of sorting Niuniu girls in ascending order of temper index
(2) The algorithmic process of handling a case
The algorithm idea is expressed as pseudo code, and the process is as follows.
COW-SORTING(a)
n←length[a], count←0
copy a to b
SORT(b)
amin←b[1]
while n>0
do j←a Subscript of the first non-0 element in
ti←∞, sum←a[j]
k←1, ai←a[j]
a[j]←0, n←n-1
while b[j]≠ai
do k←k+1
sum←sum+b[j]
if ti>b[j]
then ti←b[j]
j←FIND(a, b[j])
a[j]←0, n←n-1
if k>1
then count←count+sum+min{(k-2)*ti, (k+1)*amin}
return count
Algorithm 1-12 the algorithm process of calculating the minimum cost of rearranging Niuniu girls in ascending order of temper index
In the algorithm, set b as the result of array a sorted in ascending order (lines 2 ~ 3). a. The correspondence between b elements is determined according to the corresponding subscript, that is, a [i] σ b [i] (1 ≤ I ≤ n) the while loop of lines 5 ~ 18 repeatedly constructs a rotation subset of a each time, calculates the minimum cost of completing the element exchange of this subset, and accumulates it into the counter count (initialized as 0 in line 1). Specifically, line 6 takes the subscript j of the element not accessed in a (the element accessed in a is set to 0) and sets the first element ai rotated on the new subset. The while loop in lines 10 ~ 15 repeats according to the condition b[j] ≠ ai to construct a rotation subset. Once the condition is false (b[j]=a i), it means that the rotation is completed. In the construction process, the number of subset elements k in line 11 increases by 1, the newly discovered elements in line 12 are added to sum (line 7 is initialized as the first element ai of the subset), and lines 13 ~ 14 track the minimum element ti of the subset (line 7 is initialized as ∞). FIND the next corresponding element subscript j in line 15, set the accessed a[j] to 0 in line 16, and subtract the number of elements n (the number of elements initialized as a in line 1) that have not been accessed by 1. Once the construction of a rotation subset is completed (the while loop of lines 10 ~ 16 ends), lines 17 ~ 18 determine the added value of count according to the formula previously discussed according to whether the number of subset elements k is greater than 1. The running time of the algorithm depends on the number of times the operations in lines 11 ~ 16 are repeated. Since the value of one element in a is 0 every time, and the outer loop condition is that the number of non-0 elements in a is n > 0, the operations on lines 11 ~ 16 must be repeated several times n (i.e. the number of Niuniu). In each operation from lines 11 to 16, line 15 calls the FIND process to FIND the element subscript with value b[j] in a, which will take O(N) time, so the running time of the whole algorithm is O(N2).
#include <iostream>
#include <fstream>
#include <vector>
#include <algorithm>
using namespace std;
int cowSorting(vector<int> &a)
{
int cost = 0;
int n = int(a.size());
vector<int> b(a);
sort(b.begin(),b.end());
int a_min = b[0];
while(n > 0)
{
int j = 0;
while(a[j] == 0)
j++;
int ti = INT_MAX,sum = a[j];
int k = 1,ai = a[j];
a[j] = 0;n--;
while(b[j] != ai)
{
k++;
if(ti > b[j])
ti = b[j];
sum += b[j];
j = int(distance(a.begin(),find(a.begin(), a.end(), b[j])));
a[j] = 0;n--;
}
if(k > 1)
{
int mi = min((k - 2) * ti, ti + (k + 1) * a_min);
cost += (sum + mi);
}
}
return cost;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int n;
inputdata >> n;
while(n)
{
vector<int> a(n);
for(int i = 0;i < n; i++)
inputdata>>a[i];
int result = cowSorting(a);
outputdata <<result<<endl;
cout<<result<endl;
inputdata>>n;
}
inputdata.close();
outputdata.close();
return 0;
}
Data collection and information search
Collection and its dictionary operations
Question 2-1 open source projects
Problem description
The open resource seminar was held in a famous university. The heads of open source projects pasted the project registration form on the wall. The name of the project is located at the top of the sign form in capital as the logo of the project. Students who want to join a project sign in under the project name with their own user ID. A user ID is a string that begins with a lowercase letter followed by a lowercase letter or number.
Then the organizer takes all the signatures off the wall and enters the information into the system. Your task is to summarize the students on each project check-in form. Some students are too enthusiastic and sign their names on the project signature sheet many times. It doesn't matter. In this case, the student can count only once. Each student is required to sign up for only one project. Any student who signs up for more than one project will be disqualified.
There are up to 10000 students and up to 100 projects in the school.
input
The input contains several test cases. Each case takes a line containing only 1 as the end flag and a line containing only 0 as the end flag. Each test case contains one or more project signatures. A project signature line has a line as the project name, followed by several student user IDs, one for each line. Output for each test case, output the summary of each project. The summary data is a project name followed by the number of students enrolled in each line. These data lines should be output in ascending order of the number of students enrolled. If there are two or more projects with the same number of registered students, they shall be arranged according to the dictionary order of project names
sample input
UBQTS TXT
tthumb
LIVESPACE BLOGJAM
hilton
paeinstein
YOUBOOK
j97lee
sswxyzy
j97lee
paeinstein
SKINUX
1
0
sample output
YOUBOOK 2
LIVESPACE BLOGJAM 1
UBQTS TXT 1
SKINUX 0
Problem solving ideas
(1) Data input and output
According to the format of the input file: it contains several test cases, with "0" as the input end flag. The input data for each case contains several lines of data describing multiple projects. The first line of each project is the capitalized project name, followed by several lines of student signatures under the project. Take "1" as the end flag of case data. From the beginning, read each line in the input file in turn and store it in array a. In case of "1", end the data input of this case, calculate the final legal number of student signatures of each item in the case, and write the calculated data into the output file according to the output format requirements. Cycle until "0" is read.
Open input file inputdata Create output file outputdata from inputdata Read a line from to s while s≠"0" do Create an empty collection a while s≠"1" do APPEND(a, s) from inputdata Read a line from to s p←OPEN-SOURCE(a) for each project∈p do take"name[project] number[project] "Write as one line outputdata from inputdata Read a line from to s close inputdata close outputdata
Among them, line 9 calls the process of calculating the number of students under each open source project, OPEN-SOURCE(a), which is the key to solving a case.
(2) The algorithmic process of handling a case
For a test case, each open source project not only identifies the name of the project, but also corresponds to several student signatures. If a student has multiple signatures in a project, it is counted only once. Each student can only sign in one item. If the signature of a student appears in multiple items in the input data, the signature will be deleted from all items containing the student's signature. The final summary is the number of Students in each project. To solve a case, you can set up two sets: Projects and Students. The collection Projects is used to store the information of each project, including the project name and the number of student signatures of the project. That is, each element in Projects is an ordered pair < name, number >. Where name is the primary key, that is, the names of no two elements in Projects are the same. The element stored in the set Students is student, which contains the triple < userid, pname, deleted >, composed of the student's signature userid, the project name pname to which he belongs and the flag deleted. Where userid is its primary key. These collections can be maintained as array A is scanned. Specifically, when a project name is scanned, a sequence pair project = < project name, 0 > is created. Connect every student ID suerid scanned, and check whether there are triples < userid, pname, deleted > = student in Students. If it does not exist, it means that the student signs for the first time, add < userid, name [PROJECT], false > to Students, and increase number [project] by 1. If there is a student in Students and pname[student] ≠ name [PROJECT], deleted[student] = false, it means that the student has signed in other Projects and detected it for the first time, then subtract 1 from the number attribute value of the element with pname[student] in Projects (indicating that the student's signature is deleted from it), And change deleted[student] to true. Other situations, including pname[student] = name project Or pname[student] ≠ name[project] and deleted [student] = true (repeated signatures on multiple Projects have been investigated and dealt with), the student's signature will be ignored. Cycle until the full a is scanned. Finally, it is sorted in descending order by the number attribute value of the elements in Projects and returned as the return value. The process of writing pseudo code is as follows.
OPEN-SOURCE(a) Z Handle a case Projects←∅, Students←∅n←length[a], i←1while i≤n do project←<a[i], 0> i←i+1 while a[i]Process 1 item for student signature do userid←a[i] student←FIND(Students, userid) if student∉Students Signed as userid My students are the first to appear then INSERT(Students, < userid, project.name, false>) number[project]←number [project] +1 else if pname[student] ≠ name[project] and deleted [student]=false then deleted[student]←true p←FIND(Projects, pname[student]) DELETE(Projects, p) Z stay projects Delete element from number[p]← number [p]-1 Number of people modified INSERT(Projects, p) Rejoin i←i+1INSERT(Projects, project)SORT(Projects)return Projects
Algorithm 2-1 summarizes the number of applicants for each open source project
Consider algorithm 2-1, in which there are two sets: the project group set Projects created in line 1 and the student signature set Students. The algorithm operates on these sets as follows:
1 insert (add) the element into the collection, and call the procedure insert (Students, < userid, project. Name, false >) on line 10 to insert the triple < userid, project Name, false > add to the student signature set Students line 17 INSERT(Projects, p) add p to the project Projects line 19 INSERT(Projects, project) add the current project to the project set Projects.
2 delete the specified element from the collection. Line 15 calls the procedure DELETE(Projects, p) to delete project p from the project collection Projects.
3 find a specific value element in the collection. Line 8 calls the procedure FIND(Students, userid) to find the element with the signature of userid in the student collection students, and line 14 finds (Projects, pname[student]) to find the element with the project name of pname[student] in the Projects.
4 arrange the elements in the set in order. In line 20, SORT(Projects) arranges the elements in Projects in descending order according to the number of people in the project. If the number of people in two or more Projects is the same, they are arranged according to the dictionary order of project names.
Generally, the 1, 2 and 3 operations of the set INSERT, DELETE and FIND are called dictionary operations, and the set that implements dictionary operations is called a dictionary. According to this concept, Projects and Students are dictionaries. The fourth SORT operation is called sorting. Sorting operation can only be performed on total order set 1.
If there are n items in a case and the average number of students enrolled in each item is m, the operations in lines 7 ~ 18 will be repeated nm times. However, we cannot assert that the running time of algorithm 1 is Θ (nm) because it contains dictionary operations on each set. In addition, we need to consider the time required for sorting Projects in line 20.
In the computer, the set has various representations. Corresponding to different representations, the above four operation methods are different, which of course affects the time required for each operation.
Linear table representation of sets
The elements in the set are arranged in a row, and each element is retrieved by its location (subscript) - expressed as a linear table, as shown in Figure 2-1. Because the elements in the linear table are retrieved by their location, they can be used to represent a set of reusable elements (there can be multiple elements with the same value in the set). Find the element with a specific value of X in a linear table A={a1,a2,..., an} and operate FIND(A, x). The algorithm detects each element one by one from a 1 in a until a certain ai=x is encountered for the first time, or no element satisfying the condition is found in the whole linear table.
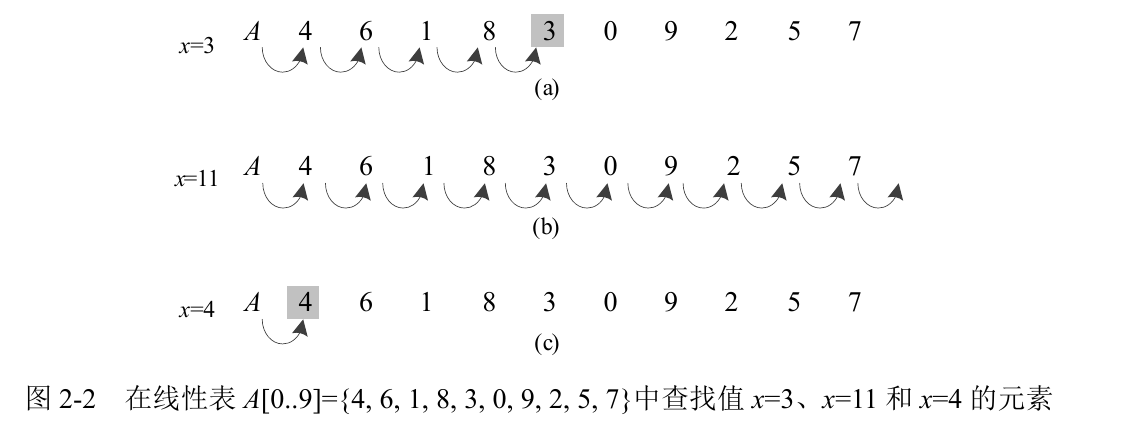
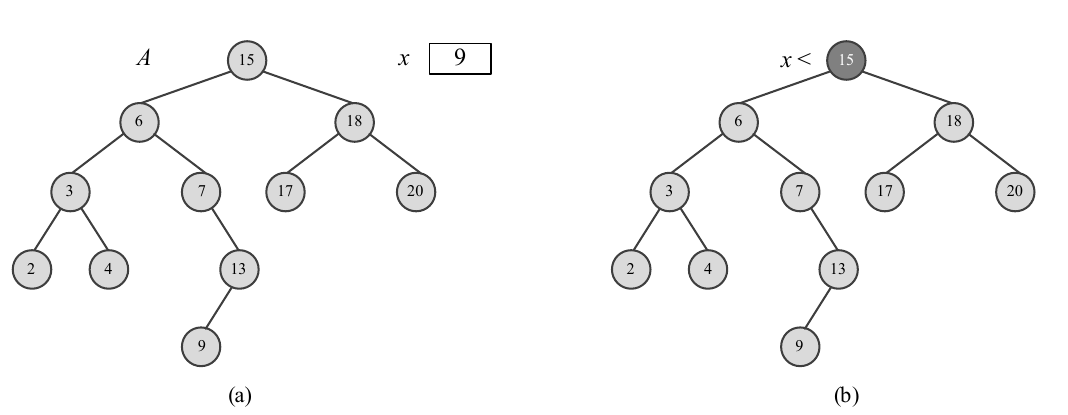
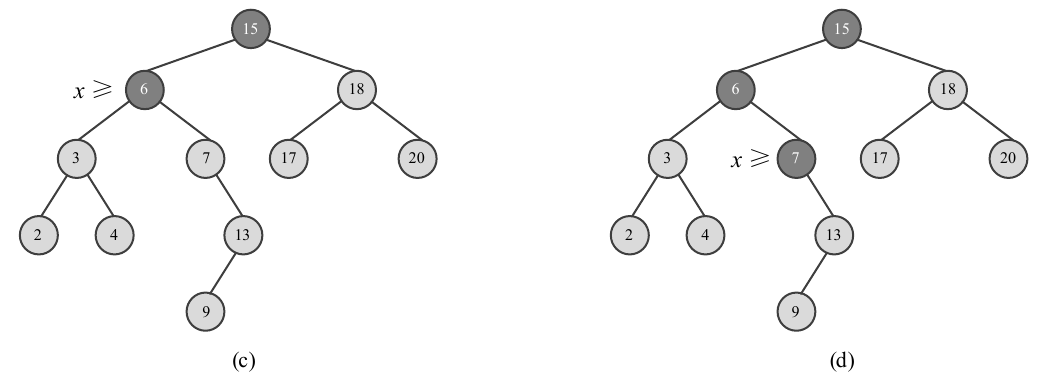
Figure 2-2 shows various situations of running FIND(A, x) when looking for elements with values x=3, x=11 and x=4 in the linear table A={4, 6, 1, 8, 3, 0, 9, 2, 5, 7}. The arc with arrow in the figure indicates sequential detection. Figure (a) shows that when x=3, the specific value element is found and detected for 5 times; Figure (b) shows that when x=11, no specific value element is found and detected 11 times, which is the worst case; chart © When x=4, the specific value element is found after one detection, which is the best case. It can be seen that the running time of the algorithm for finding the element with a specific value of X in a linear table with n elements is O(n).
The running time efficiency of INSERT and DELETE operations in linear tables is different depending on the storage mode of the table in memory. Linear lists are often represented in memory as arrays (continuous storage) or linked lists (connecting adjacent elements through pointers).
Figure 2-3(a) shows the operation of inserting data 8 into the third and fourth elements of the array (i.e. elements with values of 1 and 3). This requires that all elements after the third element (together with the third element) be moved back one position. Figure 2-3(b) shows the operation to DELETE the third element in the array (that is, the element with value 1) from the array. This requires moving all elements after the fourth element (along with the third element) forward by one position. It can be seen that for arrays, whether INSERT or DELETE, the required running time is O(n).
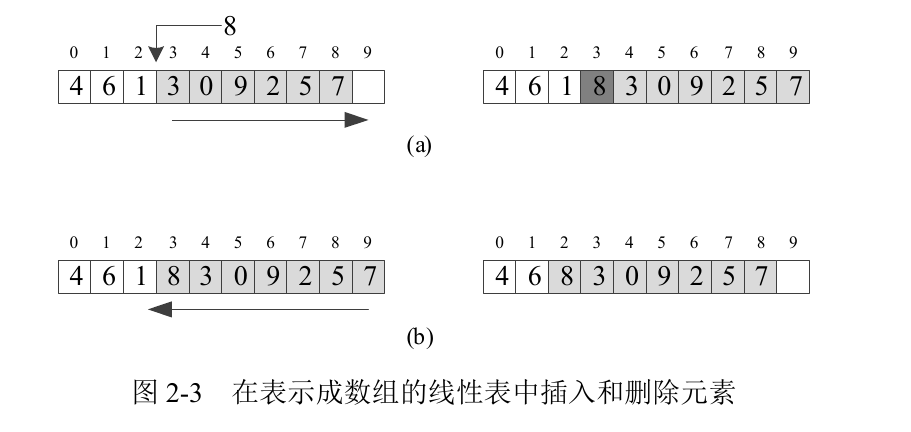
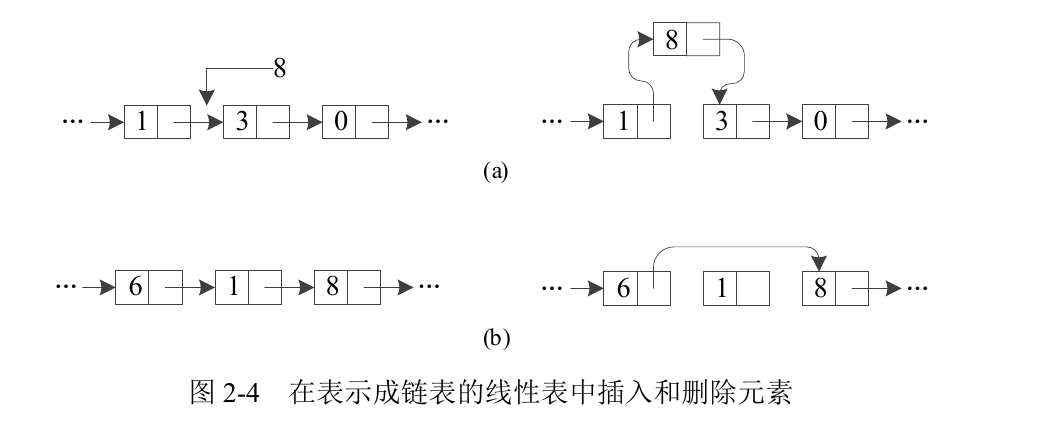
Figure 2-4(a) shows the operation of inserting an element with a value of 8 between two adjacent nodes (i.e. nodes with values of 1 and 3) in the linked list. Just point the pointer to the next node in the node with value 1 to the new node, and point the pointer to the next node in the new node to the node with value 3. Figure 2-4(b) shows the operation of deleting the node with value 1 between the nodes with value 6 and 8 in the linked list. You only need to point the pointer field of the node with value 6 to the node with value 8. It can be seen that the INSERT and DELETE operations on the linked list only take a constant time.
For the sorting operation of total ordered set represented by linear table (whether array or linked list), there are many distinctive algorithms, such as bubble sorting, insertion sorting, merge sorting, quick sorting, and so on. Theory has proved that as long as it is a sorting algorithm based on comparison between elements, the running time must not be less than n l g n 2 nlgn^2 nlgn2.
Binary search tree 3 representation of totally ordered sets
Totally ordered data sets can also be represented as binary search trees. In this binary tree, the left child's value does not exceed the father's value, while the father's value is less than the right child's value. Because the nodes in the binary search tree are retrieved according to the values of elements, the binary search tree can only represent a set without multiple elements (the values of elements in the set are different).
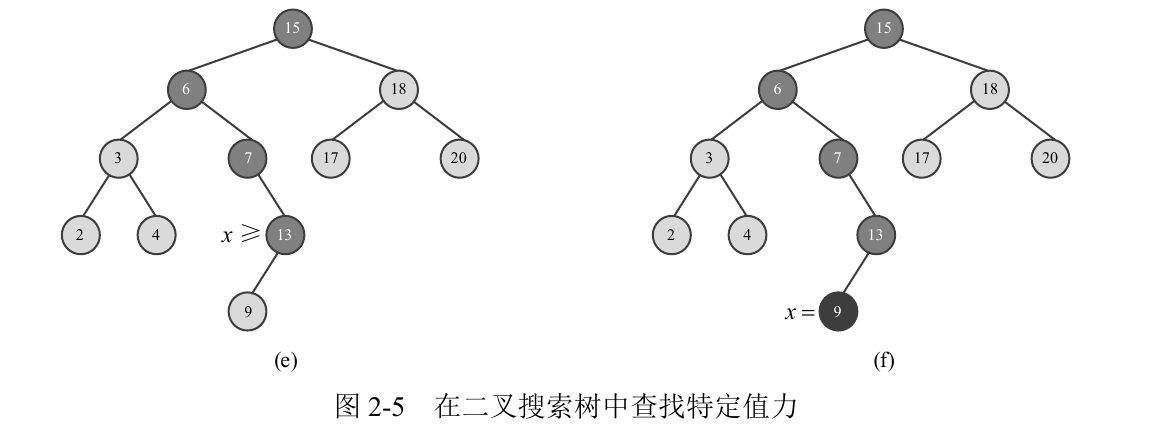
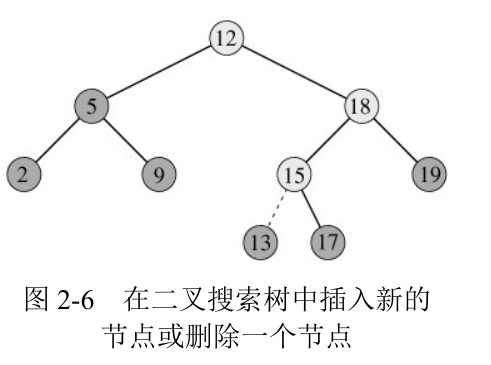
In order to find a node equal to the specific value x in the set represented as binary search tree T, compare x with the node value from the root of the tree. If it is equal, the search is successful. If x is less than the node value, continue to search in the left subtree of the node; If x is greater than the node value, continue searching in the right subtree of the node until it is found or cannot continue (there is no subtree for the current node to continue searching). As shown in Figure 2-5. The worst case is that there is no specified value node in the tree, which needs to query from the root to a leaf (node without children). The time taken will not exceed the height of tree t. If the binary search tree T with n nodes is balanced (the height of the left and right children is the same), its height is lgn. Therefore, the running time of FIND(T, x) is O(lgn). To insert a node with a value of X into the binary search tree and keep it as a binary search tree, as with the search method, first find the insertion position, and then point the child pointer of the parent node to the new node. The required time is also O(lgn). As shown in Figure 2-6.
Similarly, we can delete a node in the binary search tree in O(lgn) time to keep it as a binary search tree 4. For a set represented as a binary search tree, a sort of the set can be obtained by performing a "middle order traversal". The so-called middle order traversal starts from the root, first lists each node in the left subtree, then lists the root at the end of these nodes, and then lists each node in the right subtree. In this way, each node is accessed once, so SORT(T) takes time Θ (n).
Hash table representation of an integer set
The element value is A non negative integer or A set A that can be converted to A non negative integer, and can also be expressed as A hash table. The so-called hash table body is an array H[0... M − 1], in which each element is A linked list. Each element X in set A maps its value to an integer I in 0~m − 1 through A hash function, that is, hash(x)=i, 0 ≤ I < M. And store the element in the linked list represented by H[i], as shown in Figure 2-7. If the hash function can evenly distribute the elements in A in the M linked lists of H, it can ensure that the hash table is used as A data dictionary, and its three dictionary operations are constant time. From the structure of the hash table, it can be seen that the data set represented as A hash table cannot be sorted. Compare the running time of dictionary operation and sorting operation with the array, linked list, binary search tree and hash table discussed above, and summarize it as table 2-1.

Table 2-1
Comparison of dictionary operation and sorting algorithm running time of various data structures
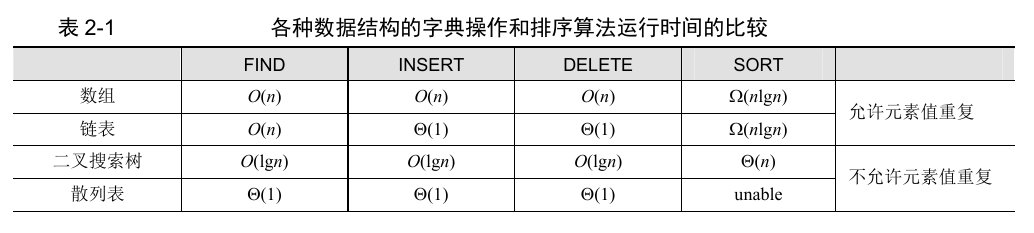
Back to algorithm 2-1. If the set students is represented as a hash table, the time consumption of FIND(Students, userid) in line 8 and insert (students, < userid, name [PROJECT], false >) in line 10 is as follows according to table 2-1 Θ (1). Since they are located in the inner cycle, the total time of these operations is O(nm). Since the collection Projects will be sorted in line 20, it is appropriate to represent it as a binary search tree. Thus, FIND(Projects, pname[student]) in line 14, DELETE(Projects, p) in line 15 and INSERT(Projects, p) in line 17 know the average time consumption O(lgn) according to table 2-1. Similarly, since these operations are located in the inner loop, the total time is O(nmlgn). Since the INSERT(Projects, project) in line 19 is located in the outer loop, the total time is O(nlgn). SORT(Projects) in line 20, according to table 2-1, the time consumption is Θ (n). Therefore, we conclude that the set Projects table is a binary search tree, the set students table is a hash table, and the running time of algorithm 2-1 is O(nmlgn). The C + + implementation code of the algorithm to solve this problem is stored in the folder laboratory/Open Source, and readers can open the file opensource CPP study and trial run.
#include <fstream>
#include <string>
#include <map>
#include <set>
#include <iostream>
#include <iterator>
#include <algorithm>
#include <vector>
using namespace std;
struct Project//Project data type
{
string name;
int number;
Project(string aname = "", int n = 0)
: name(aname), number(n) {}
};
bool operator==(const Project &a, const Project &b)
{
//A comparison operation used to find in a collection of items
return a.name == b.name;
}
bool operator<(const Project &a, const Project &b)
{
//A comparison operation used to sort a collection of items
if (a.number > b.number)
return true;
if (a.number < b.number)
return false;
return a.name < b.name;
}
ostream &operator<<(ostream &out, const Project &a)
{
//The operation used to output the elements in the project collection
out << a.name << " " << a.number;
return out;
}
struct Student
{
string pName;
bool deleted;
Student(string projectName = "", bool isDeleted = false)
: pName(projectName), deleted(isDeleted) {}
};
set<Project, less<Project>> openSource(vector<string> &a)
{
map<string, Student> students;
set<Project, less<Project>> projects;
int n = a.size(), i = 0;
while (i < n)
{
Project project(a[i++]);
while (i < n && a[i][0] >= 'a' && a[i][0] <= 'z')
{
string userid = a[i];
Student student = students[userid];
if (student.pName == "")
{
students[userid] = Student(project.name, false);
project.number++;
}
else if ((student.pName != project.name) && (!student.deleted))
{
set<Project>::iterator p = find(projects.begin(), projects.end(), Project(student.pName));
Project q(p->name,p->number - 1);
projects.erase(p);
projects.insert(q);
}
i++;
}
projects.insert(project);
}
return projects;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
string s = "";
getline(inputdata, s);
while (s != "0")
{
vector<string> a;
while (s != "1")
{
a.push_back(s);
getline(inputdata, s);
}
set<Project, less<Project>>projects = openSource(a);
copy(projects.begin(), projects.end(), ostream_iterator<Project>(outputdata, "\n"));
copy(projects.begin(), projects.end(), ostream_iterator<Project>(cout, "\n"));
getline(inputdata, s);
}
inputdata.close(); outputdata.close();
return 0;
}
Question 2-2 Prince's problem
Problem description
Prince Ray wants to marry his beautiful girlfriend Princess Amy. Amy loves Ray very much and is very willing to marry him. However, Amy's father, StreamSpeed, is a very persistent person. He thought his son-in-law should be smart enough to make him king after he retired. So he had to give Ray a test.
The king gave Ray a size of n × n × N's cube, which contains n × n × N small lattices, each lattice can be expressed as a triple (x, y, z) (1 ≤ x, y, Z ≤ n), and there is a number in each lattice. Initially, the number in all grids is set to zero
King StreamSpeed will do the following three operations on the Rubik's cube
1 add a number to the specified small cell.
2 subtract a number from the specified small cell.
3 query the sum of all numbers from lattice (x1,y1,z1) to lattice (x2,y2,z2).
(x1≤x2, y1≤y2, z1≤z2)
As Ray's good friend and an excellent programmer, you should write a program for ray to answer all queries,
Help Ray marry his dream lover.
input
The first line of input contains an integer n(1 ≤ n ≤ 100), indicating the size of the cube. Then there are several rows of data in the following format:
A x y z num: means adding a number num to the lattice (x, y, z).
S x y z num: means subtracting a number num from the lattice (x, y, z).
Q x1 y1 z1 x2 y2 z2: indicates the sum of the numbers in the grid from (x1, Y1, z1) to (X2, Y2, Z2).
The number involved in all queries will not exceed 1000000. The input file ends with a line of data containing only 0
0 does not require any processing.
output
For each query in the input file, the program should output the corresponding result - the sum of the numbers in the range (x1, y1, z1)~(x2, y2, z2). All results do not exceed 1 0 9 10^9 109.
sample input
10
A 1 1 4 5
A 2 5 4 5
Q 1 1 1 10 10 10
S 3 4 5 34
Q 1 1 1 10 10 10
0
sample output
10
-24
Problem solving ideas
(1) Data input and output
According to the description of the input file format of this question, you need to read the magic cube scale n from the input file first. Then read each row of instructions and store the instructions in string array a until only one row containing "0" is read. Calculate the impact of executing each instruction in a on the data in each grid in the magic cube, and record the query result of executing the query instruction in the array result. Write the elements in the result to the output file one per line.
Open input file inputdata Create output file outputdata from inputdata Read in n from inputdata Read a row from s Create array a while s≠"0" do APPEND(a, s) from inputdata Read one line s result←PRINCE-RAY-PUZZELE(a) for each x∈result do take x Write as one line outputdata close inputdata close outputdata
Among them, the key to solve a case is to call the process PRINCE-RAY-PUZZELE(a) to calculate the change of the magic cube state after the execution instruction sequence and return the query instruction execution result
(2) The algorithmic process of handling a case
The most intuitive idea of this problem is to use the method of solving problem 0-2 for reference, use A three-dimensional array BRICK[1... n, 1... n, 1... n] to represent the big magic cube, and initialize each element to 0. Add each A operation: BRICK[x, y, z] ← BRICK[x, y, z]+num; Subtract each S operation: BRICK[x, y, z] ← BRICK[x, y, z]+num; For each Q operation, traverse the three-dimensional area determined by the diagonal (x 1, Y1, Z 1) − (x 2, Y2, Z2), accumulate the data of each square BRICK[x, y, z] and output:
sum←0 for x←x 1 to x2 do for y←y1 to y2 do for z←z1 to z2 do sum←sum+BRICK[x, y, z] output sum
Assuming that the number of instructions is equal to n and the instruction types are balanced (the number of A, S and Q instructions is equal), the time to solve this problem is O(n4). In order to improve time efficiency, we make the following modifications. Treat each small cell in the magic cube as A quadruple < x, y, Z, number >, and maintain A sequence BRICK (initialized as an empty set) with such A quadruple element type. For each A or S operation, if (x, y, z) representing the grid position appears for the first time, insert (BRICK, < x, y, Z, Num >), otherwise, add or subtract. For the Q operation, traverse the sequence BRICK, accumulate the number attribute of the element < x, y, Z, number > that satisfies the conditions: x1 ≤ x ≤ x2,y1 ≤ y ≤ Y2, Z1 ≤ Z ≤ z2, and output it. Described as the following pseudo code process
PRINCE-RAY-PUZZELE(a) BRICK←∅, result←∅ m←length[a] for i←1 to m do read command from a[i] if command="A" or "S" Add or subtract instruction then read <x, y, z, num> from a[i] cell←FIND(BRICK, <x, y, z >) if cell∉BRICK then if command ="A" then APPEND(BRICK, <x, y, z, num>) else APPEND(BRICK, <x, y, z, - num>) else if command ="A" then number[cell] ← number[cell] +num else number[cell] ← number[cell] -num else read x1, y1, z1, x2, y2, z2 from a[i] Z Query instruction Q sum←0 for each <x, y, z, number> ∈BRICK Z ergodic BRICK do if x1≤x≤x2 and y1≤y≤y2 and z1≤z≤z2 then sum←sum+number APPEND(result, sum) return result
Algorithm 2-2 algorithm process for solving the "Prince's problem"
Still assuming that the number of instructions m is equal to N, the for loop on lines 3 to 20 will repeat Θ (n) Times. Each time you repeat the operations in lines 4 to 14, the time consumption can be regarded as Θ (n). This is because line 6 performs the search operation in BRICK. According to table 2-1, this requires Θ (n) Time. The insertion operation in BRICK in line 10 or 11 takes a constant time if the element is appended to the end of the sequence. The traversal of BRICK in lines 17 to 19 takes time Θ (n). In short, the running time of algorithm 2-2 is Θ (n2). The C + + implementation code of the algorithm to solve this problem is stored in the folder laboratory/ Prince Rays Puzzle
#include <iostream>
#include <fstream>
#include <sstream>
#include <list>
#include <string>
#include <vector>
#include <iterator>
#include <algorithm>
using namespace std;
class Tetrad
{
public:
int x,y,z,number;
Tetrad(int a, int b, int c, int d = 0): x(a), y(b), z(c), number(d) {}
};
bool operator==(const Tetrad &a,const Tetrad &b)
{
return a.x == b.x && a.y == b.y && a.z == b.z;
}
vector<int> princeRayPuzzle(vector<string> a)
{
list<Tetrad>BRICK;
vector<int> result;
int m = a.size();
istringstream strstr;
for(int i = 0;i < m; i++)
{
strstr = istringstream(a[i]);
string cmd;
strstr>>cmd;
list<Tetrad>::iterator cell;
if(cmd == "A" || cmd == "S")
{
int x, y, z, num;
strstr >> x >> y >> z >> num;
cell = find(BRICK.begin(), BRICK.end(), Tetrad(x,y,z));
if(cell == BRICK.end())
BRICK.push_back(Tetrad(x, y, z, cmd == "A" ? num : -num));
else
cell->number = cell->number + (cmd == "A" ? num : -num);
}
else
{
int x1, y1, z1, x2, y2, z2, sum = 0;
strstr >> x1 >> y1 >> z1 >> x2 >> y2 >> z2;
for(cell = BRICK.begin();cell != BRICK.end(); cell++)
if((cell->x >= x1 && cell->y >= y1 && cell->z >= z1) && (cell->x <= x2 && cell->y <= y2 && cell->z <= z2))
sum += cell->number;
result.push_back(sum);
}
}
return result;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int n;
inputdata >> n;
vector<string> a;
string s;
getline(inputdata,s);//Break line
getline(inputdata,s);
while(s != "0")
{
a.push_back(s);
getline(inputdata,s);
}
vector<int> result = princeRayPuzzle(a);
copy(result.begin(), result.end(), ostream_iterator<int>(outputdata, "\n"));
copy(result.begin(), result.end(), ostream_iterator<int>(cout, "\n"));
inputdata.close();
outputdata.close();
return 0;
}
Question 2-3 degree bear is the first to play
Problem description
A fashion show was arranged for Baidu's annual meeting. N employees will perform on the stage in full dress. The order of performances is determined by a "line drawing" lottery
First, employees draw N parallel vertical lines on a piece of white paper. At the top of the vertical line, write down the number of employees from 1 to N from left to right; Under the vertical line, write 1 to N from left to right to represent the order of performance
Then, employees randomly add a horizontal line segment perpendicular to the vertical line between two adjacent vertical lines.
Finally, the exit order of each employee is determined according to the following rules: each employee starts from his own number and draws his finger down the vertical line. Whenever he encounters a horizontal line, he moves to the adjacent vertical line until his finger reaches the exit order number below the vertical line. At this time, the number pointed by the finger is the appearance order of the employee. For example, in the example shown in the figure below, Dudu bear will be the second to appear, and the first to appear is employee 4.
When drawing horizontal lines, employees will avoid drawing lines repeatedly at the same position and avoid connecting two adjacent horizontal lines together, that is, the situation shown in the figure below will not occur.
Given a line drawing scheme, Dudu bear with employee number K wants to know whether he is the first to perform. If not, Dudu bear wants to know if he can make himself the first to perform by adding a horizontal line segment.
input
For the convenience of description, we stipulate that the direction with employee number is the positive direction of Y axis (i.e. above the vertical line in the above), the direction with exit order is the negative direction of Y axis (i.e. below the vertical line in the above), and the vertical line is numbered from 1 to N along the positive direction of X axis (i.e. from left to right in the above). Therefore, the position of each horizontal line can be determined by a triple (xl, xr, y), where xl, xr is the number of the vertical line where the left and right ends of the horizontal line are located, and Y is the height of the horizontal line. The first line of input is an integer T(T ≤ 50), representing the number of groups of test data. The first row of each group of data contains three integers N, M and K (1 ≤ N ≤ 100,0 ≤ M ≤ 1000,1 ≤ K ≤ N), representing the number of employees participating in the performance, the number of horizontal lines drawn and the employee number of Dudu bear respectively. Rows 2~M+1 of each group of data contain three integers xl,xr,y(1 ≤ xl ≤ N,x r = xl +1,0 ≤ y ≤ 1000000), which describe the position of a horizontal line.
output
For each group of data, a line of Yes or No is output, indicating whether the bear can make itself the first performance by adding a horizontal line segment. If Dudu bear is already the first to perform, Yes is also output. Note that although the height of the horizontal line drawn by the employee in the input data is an integer, the degree bear can draw a horizontal line at any real height. In addition, like employees, Dudu bear needs to avoid repeated scribing at the same position when drawing horizontal lines, and avoid two adjacent horizontal lines connected together.
sample input
2
4 6 3
1 2 1
1 2 4
1 2 6
2 3 2
2 3 5
3 4 4
4 0 3
sample output
Yes
No
Problem solving ideas
(1) Data input and output
According to the format of the input file, first read the number of cases T, and then read the data of each case in turn. For a case, first read the integers n, m and K representing the number of employees, the number of horizontal lines and the degree bear number, and then read the data x, l, XR and y of each horizontal line in turn and place them in array a. For the input data N,M,K and a of the case, calculate and judge whether the degree bear can enter the field first by adding a horizontal line, and finally write the judgment result (Yes/No) as a line into the output file. The pseudo code is described as follows.
Open input file inputdata Create output file outputdata from inputdata Read in T for i←1 to T do from inputdata Read in N, M, K Create array a for j←1 to M do from inputdata Read in xl,xr,y APPEND(a, <xl,xr,y>) result←TO-BE-FIRST(a, N, K) take result Write as one line outpudata close inputdata close outputdata
Among them, the key to solve a case is to call the process TO-BE-FIRST(a, N, K) in line 10 to calculate and judge whether Dudu bear can get out first by adding a horizontal line.
(2) algorithm process of handling a case
Let the height of the horizontal line drawn at the highest point be L. Then the data model of the engraving problem is a two-dimensional matrix A L + 2 × N : A_{L+2×N}: AL+2×N: A [ 0.. L , 1.. N ] A[0..L,1..N] A[0..L,1..N]. A[0…L, 1…N]. Each column represents a vertical line. If there is a horizontal line segment at the height i between two adjacent vertical lines J and j+1, then A[i, j]=right(→), A[i, j+1]=left(←). In order to be consistent with the direction shown in the figure, we number the rows of the matrix in the reverse order of the top-down ordinary matrix (from bottom to top). For example, test case 1 data can be represented as 8 shown in Figure 2-8 × 4 matrix.
Using this matrix, we can find the path of any employee from top to bottom: down from the top of the vertical line with the same number J as the employee - Search downward from A[L+1, j] in column J of the corresponding matrix A. assuming that the first non down is searched at i, if A[i, j] is right, the next search should start from A[i, j+1], Otherwise, search down from A[i, j − 1]. This cycle is repeated until it reaches below the bottom of a vertical line. At this time, the column number is the sequence number of employee J. The vertical line segment passed during the scribing process is represented as a triple (yl, yu, x), where yl represents the lower end position of the vertical line segment, yu represents the upper end position of the line segment, that is, (yl, yu) represents the height of the line segment, figure 2-8 represents the symbol matrix degree interval of test case 1, and X represents the number of the vertical line where the vertical line segment is located, then the scribing path of employee J can be represented as the set path j of these triples. In particular, the scribing path pathK of the degree bear can be found. The first line at the bottom is all down, indicating the virtual exit; The eighth line at the top is all down, indicating the virtual entry.
The first line at the bottom is all down, indicating the virtual exit; The eighth line at the top is all down, indicating the virtual entry.
For example, in the above case 1, consider the degree bear No. 3. From A[7, 3], A[5, 3] = ← is searched vertically, so switch to A[5, 2]., Switch to A[4, 1]. From A[4, 1], A[1, 1] = →, so switch to A[1, 2]. Search vertically from A[1, 2] to exit A[0, 2]. In this way, the path of the degree bear can be expressed as path3={(0, 1, 2),(1, 4, 1),(4, 5, 2),(5, 7, 3)}
The search process in the opposite direction can determine the marking path of employees corresponding to each exit order. In particular, the marking path backpath1 of the first employee can be found. For example, in case 1, starting from A[0, 1], A[1, 1] = →, so switch to A[1, 2], continue to search vertically until A[2, 2] = →, and switch to A[2, 3]. Search vertically from A[2, 3] to A[4, 3] = →, and switch to A[4, 4]. Continue to search vertically from A[4, 4] until the entrance A[7, 4] is 0. In this way, the marking path of the first employee is backpath 1={(0, 1, 1), (1, 2, 2), (2, 4, 3), (4, 7, 4)}. Compare the scribing path of Dudu bear with the scribing path of employee No. 1. If there is a vertical line adjacent to each other and the height intersects, draw a horizontal line at any point of the intersection, and Dudu bear will be the first to exit. Otherwise, No. For example, in the above example, (5, 7, 3) in the medium bear marking path is adjacent to (4, 7, 4) in the marking path of employee 1, and (5, 7) ∩ (4, 7) = (5, 7). Therefore, Dudu bear can draw a horizontal line (height between 5 ~ 7) from the third vertical line to the fourth vertical line to make himself the first to appear. Of course, Dudu bear can also draw a horizontal line to the left at the bottom (0.1) of the second straight line before the exit.) There are two problems when using matrix to represent the scribing model: first, because the geometry of the highest horizontal line height is not exactly known in the design, in order to adapt to all possible case data, the number of rows of the matrix must be defined as the maximum value of 1000000 described in the question plane. Second, when the number of employees N reaches the maximum value of 100, the scale of the matrix reaches 1000 × 1000000, which is a big expense. Moreover, when searching the scribed path, the running time of the algorithm is also very extravagant. In order to improve the space-time efficiency of the algorithm, we represent the ith column in the matrix as a set linei, in which the elements are binary < height, direction >, representing the endpoint information of a horizontal line: the height and direction (left or right) of the horizontal line. The elements in linei are arranged in descending order of height. The M horizontal lines in a case correspond to 2M such triples distributed in the set line 1,line2,..., lineN. Those data representations with down direction are omitted, which reduces the space-time overhead. For a case data in the input file, the process of forming such data storage can be described as follows.
(can't understand)
Question 2-4 finding human clones
Problem description
The Texas town of dubville was attacked by aliens. Aliens kidnapped some residents of the town and escorted them to their spaceship around the earth. After a difficult time, the aliens cloned a group of prisoners and put them back to the small town of dabwilli with their copies. Therefore, there may be six identical people named Hugh F. bumblebee in the town: Hugh F. Bumblebee himself and his five copies. The FBI asked you to find out how many copies everyone in the town has. In order to help you complete your task, the Bureau of investigation has collected DNA samples from everyone. All copies of the same person have the same DNA sequence, and the DNA sequences of different people must be different (it is known that there have never been twins in the small town).
input
The input file contains several test cases. The first row of data in each case contains two integers, 1 ≤ n ≤ 20000 and 1 ≤ m ≤ 20, representing the number of people in each town and the length of each DNA sequence respectively. The next N lines represent the DNA sequence of these n individuals: each line contains A string of length m composed of the characters' A ',' C ',' G 'or'T'. The case where n=m=0 in the data is the end flag of the input data.
output
For each case, the program outputs n lines, each line containing an integer. The first line indicates the number of people without a copy, and the second line indicates the number of people with a copy. The third line indicates the number of people with two copies, and so on: the i line indicates the number of people with i-1 copies. For example, there are 11 samples in total, of which 1 is from John Smith and the other 10 are from Joe Foobar. Then the output lines 1 and 10 are 1, and all other lines are 0.
sample input
9 6
AAAAAA
ACACAC
GTTTTG
ACACAC
GTTTTG
ACACAC
ACACAC
TCCCCC
TCCCCC
0 0
sample output
1
2
0
1
0
0
0
0
0
Problem solving ideas
(1) Data input and output
According to the description of the input file format of this question, the first line of each test case contains two integers n and m representing the number of DNA strings and the length of each DNA string. Followed by N lines, one DNA string per line. n=0 and m=0 is the input end flag. Read the DNA strings in the case in turn. Since DNA strings are repetitive, it is appropriate to represent the set a composed of these strings as an array. Process a to calculate the number of clones of each DNA sample. Similarly, since the number of DNA samples with different clone numbers may be the same, it is also appropriate to organize these data into an array solution. Write each item of solution data as a line to the output file. The process of representing as pseudo code is as follows.
Open input file inputdata Create output file outputdata from inputdata Read in n and m while n>0 and m>0 do Create array a[1..n] for i←1 to n do from inputdata Read in a[i] solution←FIND-THE-CLONES(a) for each s∈solution do take s Write as one line outputdata in from inputdata Read in n and m close inputdata close outputdata
Among them, line 8 calls the process FIND-THE-CLONES(a) to calculate the number of DNA strings with different clone numbers, which is the key to solve a case.
(2) The algorithmic process of handling a case
Two sets are used to solve a test case with a given input a: one is the sample set DNAS composed of N DNA strings, in which the elements can be regarded as the sequence pair composed of DNA representing the DNA string and copies representing the number of copies of the string < DNA, copies >. The other is the set solution representing solutions, in which the elements can also be regarded as ordered pairs < copies, number >, which is used to represent the number of samples with the number of copies. It is worth noting that the value of the attribute copies of the solution element is also the sequence number when the element is output. The set DNAS can be dynamically generated by scanning the input array a[1... N]: for the current DNA string a[i], if the DNA string without sample in DNAS is a[i], add < a[i], 1 > to DNAS; Otherwise, increase the copy attribute value of the element sample = < a[i], copies > in DNAS by 1. The number of elements in the solution must be n, and the value of the element can be determined according to the element attribute copies in DNAS. The specific process is described in the following pseudo code.
FIND-THE-CLONES(a)
n←length[a], DNAS←∅
for i←1 to n
do dna←a[i]
sample←FIND(DNAS, dna)
if sample ∉DNAS
then INSERT(DNAS, <dna, 1>)
else copies[sample]←copies[sample]+1
solution[1..n]←{0, 0, ..., 0}
for each sample∈DNAS
do solution[copies[sample]]←solution[copies[sample]]+1
return solution
Algorithm 2-7 algorithm process of solving a case of "looking for human cloning"
Since the operations on the set DNAS are limited to finding and inserting, it is appropriate to represent it as a Hash table, and the first attribute copies of the element in the solution is also the output order of the element. Therefore, the value of this attribute can be used as the subscript of the element stored in the array. In other words, it is appropriate to represent the solution as an array whose element type is an integer (solution[i] represents the number of DNA strings with I copies), which is also reflected in algorithm 2-2. Thus, the running time of the algorithm is Θ (n) , this is because the for loop in rows 2 ~ 7 is repeated N times. The time-consuming of searching and inserting the Hash table DNAS is constant each time. The for loop in rows 9 ~ 10 is repeated at most N times. The time-consuming of arithmetic operation and assignment operation in the loop body is also constant. The C + + implementation code of the algorithm to solve this problem is stored in the folder laboratory/Find the Clones. Readers can open the file find the clones CPP study and trial run. For C + + code parsing, please read chapter 9.4 Description of procedure 9-43 in Section 1.
#include <iostream>
#include <string>
#include <vector>
#include <fstream>
#include <iterator>
#include <map>
using namespace std;
vector<int> findTheClones(const vector<string> &a)
{
int n = a.size();
map<string,int>DNAS;
for(int i = 0;i < n;i++)
{
DNAS[a[i]]++;
}
vector<int> solution = vector<int>(n,0);
map<string,int>::iterator dna;
for(dna = DNAS.begin();dna!=DNAS.end();dna++)
solution[dna->second-1]++;
return solution;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int n,m;
inputdata>>n>>m;
while(n!=0 || m!=0)
{
vector<string> a;
for(int i = 0;i<n;i++)
{
string sample;
inputdata>>sample;
a.push_back(sample);
}
vector<int>solution=findTheClones(a);
copy(solution.begin(), solution.end(), ostream_iterator<int>(outputdata, "\n"));
copy(solution.begin(), solution.end(), ostream_iterator<int>(cout, "\n"));
inputdata>>n>>m;
}
inputdata.close();outputdata.close();
return 0;
}
Question 2-5 crazy search
Problem description
Many people are keen on guessing puzzles and are crazy about puzzles from time to time. One such puzzle is to find a prime number related to it in a given text. This prime may be the number of different substrings of a specified length in the text. To solve this problem, it seems that we need to turn to a computer and a good algorithm. Your task is to write a program to determine the number of different substrings with length N in the text for a given text and the number of characters that make up the text. For example, for the text "daababac", NC=4 is known, and the different substrings with length N=3 in the text are: "daa", "aab", "aba", "bab" and "bac". So the answer is 5.
input
The input contains several test cases, and each case contains two rows of data: the first row contains two integers separated by a space, N and NC. Line 2 is a piece of text to search for. It is assumed that in this text composed of NC characters, the number of substrings with length n does not exceed 16000000. N=0,NC=0 is the end flag of input data.
output
The program outputs only one line of data for each test case, including only one integer representing the number of different substrings with length N in the text.
sample input
3 4
daababac
0 0
sample output
5
Problem solving ideas
(1) Data input and output
Read N and NC from the input file for each test case according to the description of the input file format, and then read the text line text. Calculate the number of different substrings with length N in text, and write the calculation result as a line to the output file. Until N=0 and NC=0 are read from the input file. The process of becoming code is as follows
Open input file inputdata Create output file outputdata from inputdata Read in N and NC while N>0 or NC>0 do from inputdata Read text lines in text result← CRAZY-SEARCH(text, N) take result Write as one line outputdata from inputdata Read in N and NC close inputdata close outputdata
Among them, line 6 calls the process of calculating the number of different substrings of a given length contained in the text line, which is the key to solving a test case.
CRAZY-SEARCH (text, N)
(2) The algorithmic process of handling a case
The essence of this problem is to calculate the set composed of all substrings with length N in text[1... Length], and count the number of elements of the set (the same substring is counted only once). Dynamically maintain the substring set s of text (initialized to ∅), and for each substring with length N, s=text i...i+N , check whether it occurs in s ∈ s. If yes, add s to s. The specific process can be expressed as the following pseudo code.
CRAZY-SEARCH(text, N) length←text Length of S←∅ for i←0 to length-N do s←text[i...i+N-1] t←FIND(S, s) if t∉S then INSERT(S, s) return S Number of elements
Algorithm 2-8 algorithm process for solving the "crazy search" problem
Here, there are only two operations for set S: FIND(S, s) and INSERT(S, s). Therefore, S can be any kind of dictionary. For dictionary operation, according to table 2-1, hash table is the most time-saving. However, the elements stored in the hash table must be non negative integers. In this problem, if the dynamic set S is represented as a hash table, the string added to it needs to be converted into a non negative integer. NC in the input indicates the number of characters constituting text. For example, text = "daabaac" in the input example is composed of four letters a, B, C and D. If a corresponds to 0,b corresponds to 1,c corresponds to 2 and D corresponds to 3, any substring of text can uniquely correspond to a quaternary integer. For example, the substring daa corresponds to 3 × 4 2 + 0 × 4 + 0 = 48 3×4^2+0×4+0=48 three × 42+0 × 4 + 0 = 48, and aab corresponds to 3 × 4 2 + 0 × 4 + 1 = 1 3×4^2+0×4+1=1 3×42+0×4+1=1,...
Thus, the running time of the process is Θ (length), that is, the length of text
#include <iostream>
#include <fstream>
#include <string>
#include <set>
using namespace std;
int cracySearch(string &text,int n)
{
set<string> S;
int length=text.length();
for(int i = 0;i<=length-n;i++)
{
string s = text.substr(i,n);
S.insert(s);
}
return S.size();
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int n,nc;
inputdata>>n>>nc;
while(n>0||nc>0)
{
string text;
inputdata>>text;
int result=cracySearch(text,n);
outputdata<<result<<endl;
cout<<result<<endl;
inputdata>>n>>nc;
}
inputdata.close();outputdata.close();
return 0;
}
Search of text string
In information processing, the problem of finding the location of a pattern in a text string often occurs. For example, text is a document being edited, and the pattern to find is a specific word provided by the user. As shown in Figure 2-9, find the first occurrence of mode P = "ABAA" in the text string T = "ABCABAABCABAC". This pattern appears only once in the text at an offset of s = 3. Each character in the pattern is connected with the matching character in the text through a vertical bar,
All matching characters are shaded. This problem is called string matching problem. Set a set of all legal characters Σ Is a finite set called the alphabet. Σ Use alphabet Σ A collection of all finite length strings composed of characters in. Zero length empty string, with ε It also belongs to Σ. We treat text and patterns in text search as Σ* String in
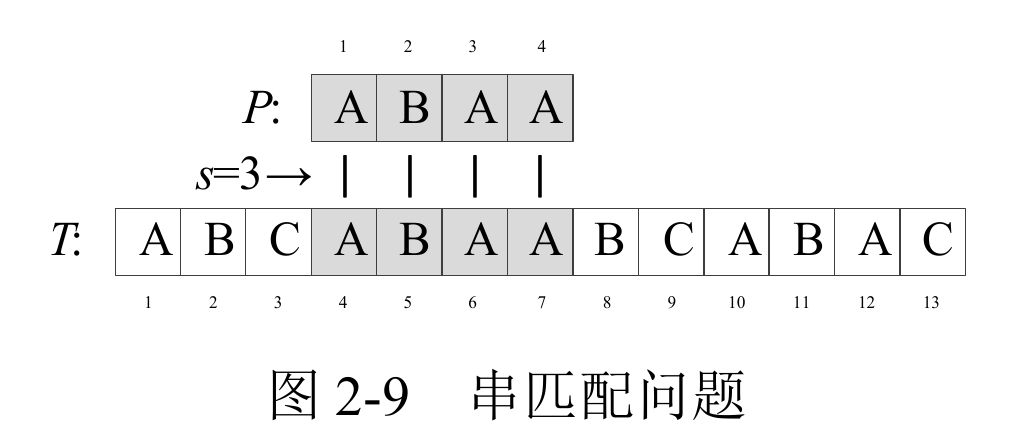
The most intuitive algorithm to solve the string matching problem for text T [1... N] and pattern P[1... M] is to use a loop to find the first effective offset by detecting whether the condition P[1... m] = T [s + 1... s + m] is true for each of n − m + 1 possible s values, as shown in Figure 2-10.
In Figure 2-10(a), the offset s=0,P[1] matches T[1] (connected by a vertical line), but P[2] ≠ T[2] encounters a mismatch (represented by a cross), and s increases by 1 to enter figure 2-10(b). In Fig. 2-10(b), s=1,P[1] ≠ T[2] encounters another mismatch, s increases by 1 and enters Fig. 2-10 ©. In Figure 2-10 © Where s=2, P[1]=T[3], P[2]=T[4], P[3]=T[5], a complete match is obtained.
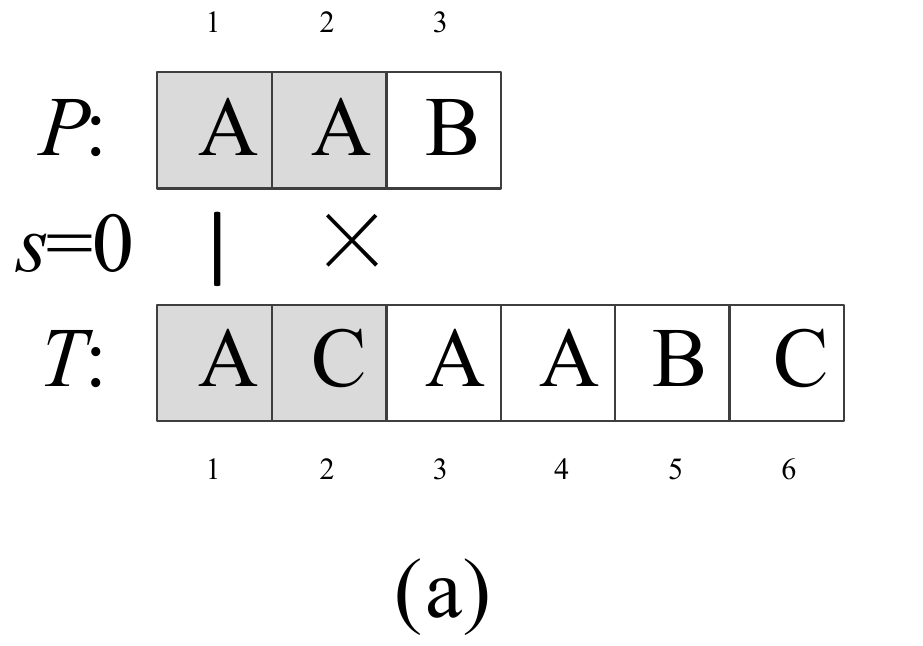
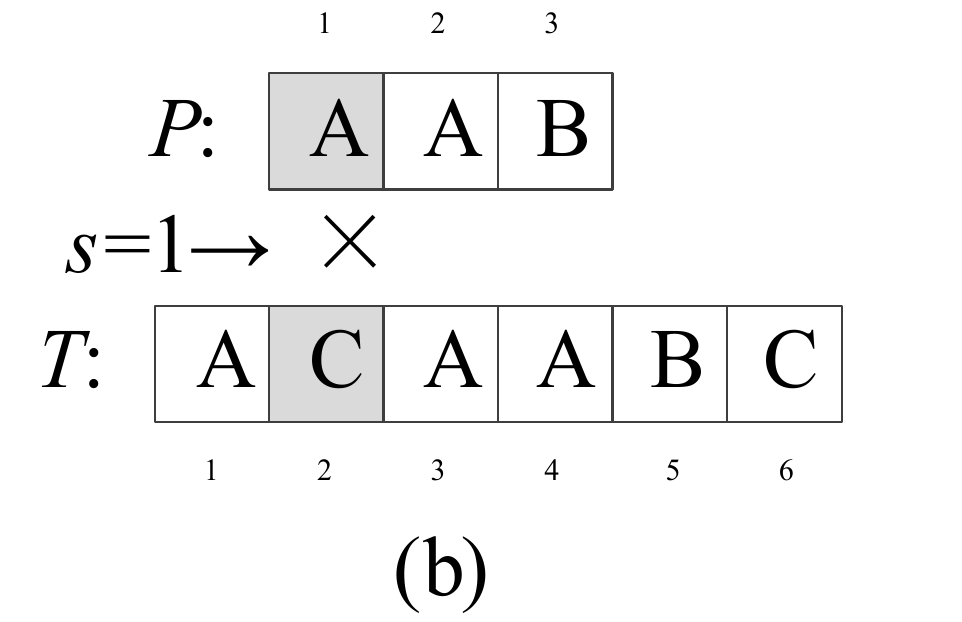
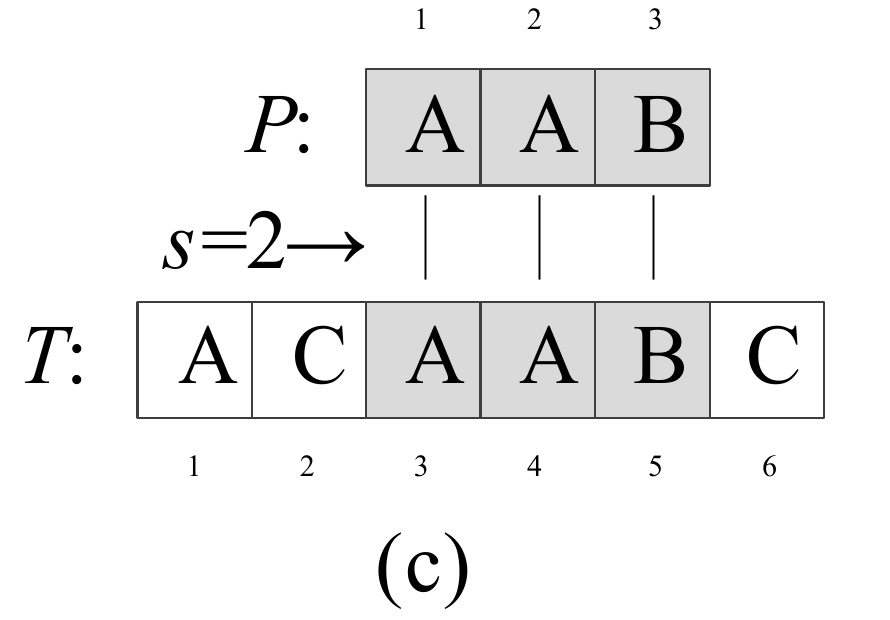
The process of describing this idea as pseudocode is as follows
STRING-MATCHER(T, P) n ← length[T] m ← length[P] for s ← 0 to n - m do k←1 while P[k] = T[s + k] do k←k+1 if k>m then return s return -1
Algorithm 2-9 powerful algorithm for calculating string matching with text T[1... n] and pattern P[1... m]
The running time of the string-match process mainly depends on the execution times of the comparison operation T[s+i]=P[i] in line 5. The worst case is that each mismatch occurs between P[m] and T[s+m], that is, m comparisons are required for the matching of n − m+1 values from 0 to n − M. Therefore, the running time is O((n − m+1) m) (see Figure 2-11). Figure 2-11 shows the execution process of the strong matching algorithm for the worst case t = "aaaaab", P = "AAB" of n = 9 and M = 4: each legal value of s (6=n − m+1 values in total: 0,1,2,3,4,5) in figure (a) to figure (f), and each element of the pattern (4 elements with shadows in total) should be compared with the corresponding text element (elements with shadows) for 6 times × 4=24.
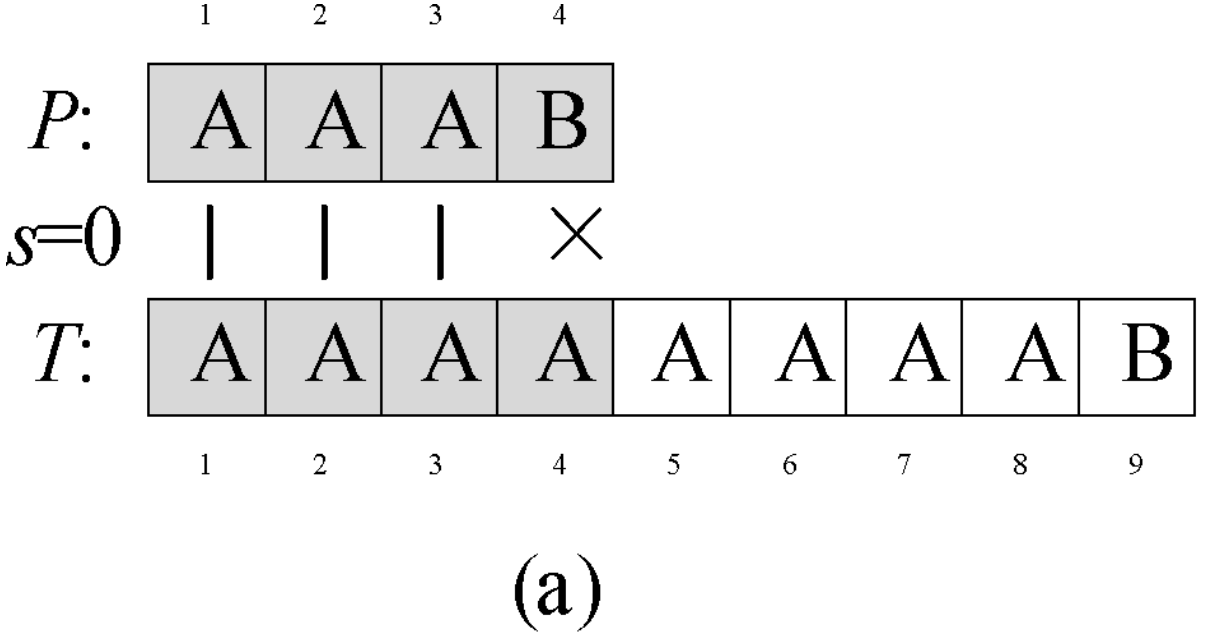
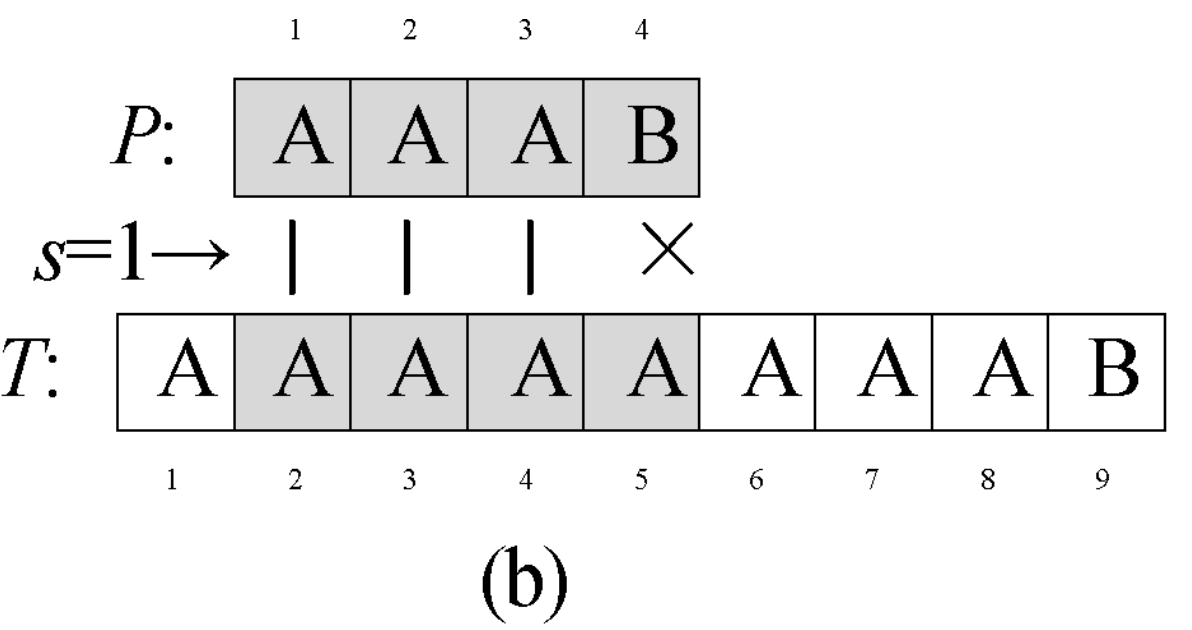
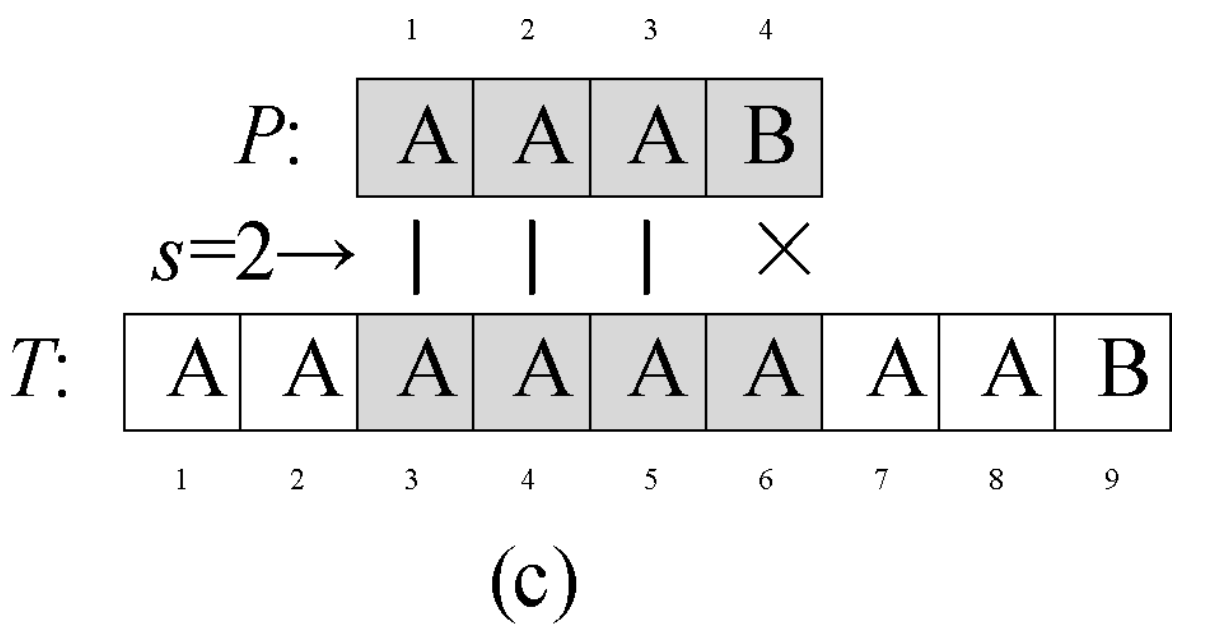
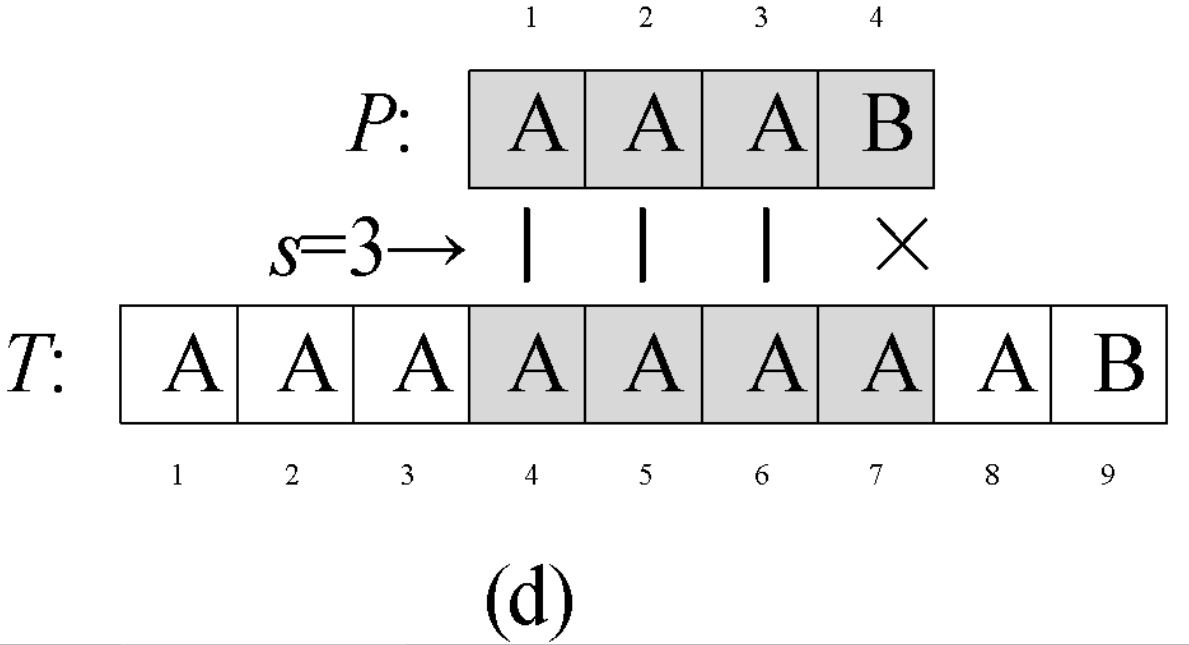
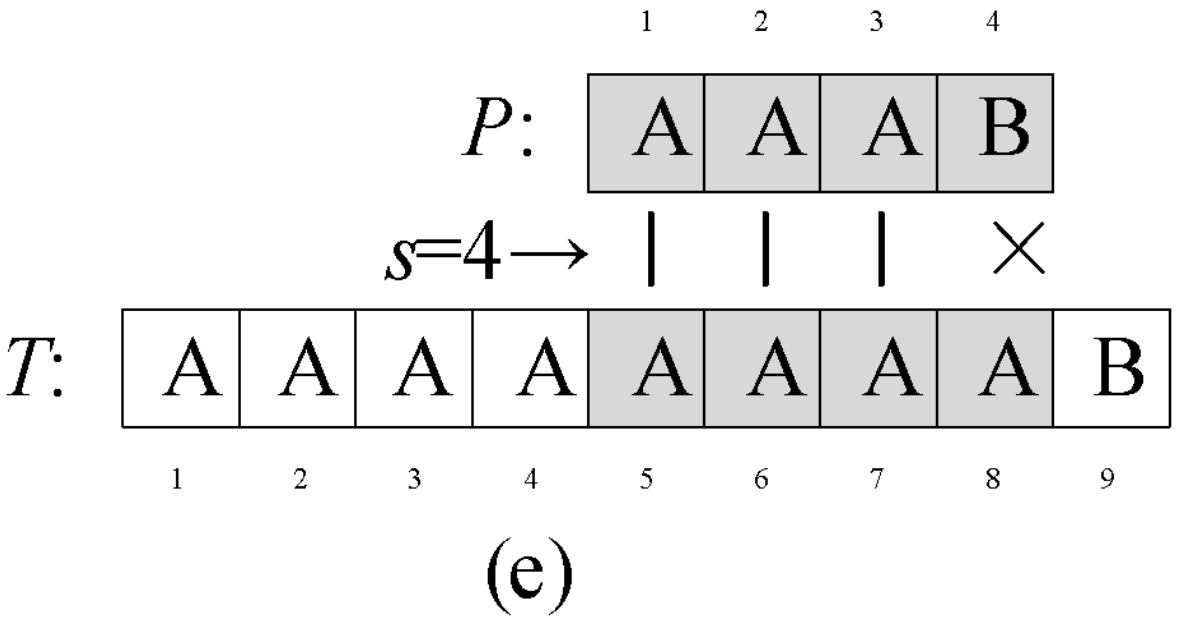
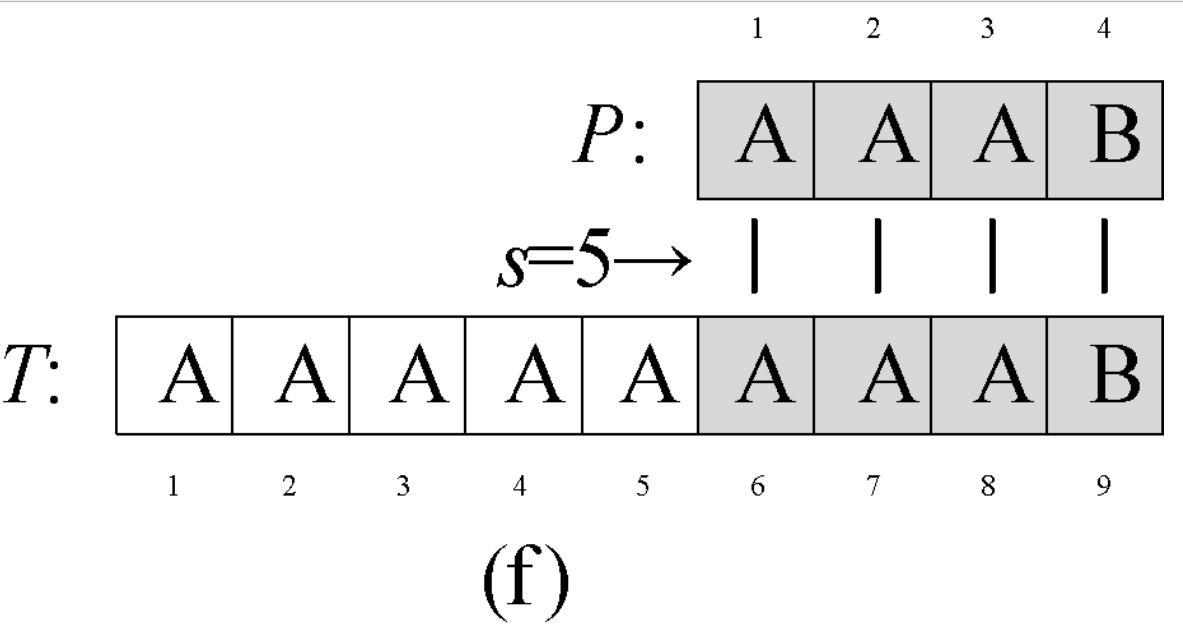
In fact, in the above example, 4 pairs of elements are not compared every time. Because in addition to comparing 4 pairs of elements in the first match, for each mismatch (the first occurs at s=0,i=4, and the last occurs at s=4,i=4), we observe that P[1... 3] in the pattern matches T[s+1... s+3] in the text, and the prefix P[1... 2] of P[1... 3] is just the suffix of T[s+1... s+3]. In this way, when we increase the offset s by 1, we know that T[s+1... s+2] matches P[1... 2], so the comparison can start with i=3. In this way, only two pairs of elements (P[3], T[s+3], P[4], T[s+4]) need to be compared, which greatly reduces the number of comparisons (see Figure 2-12).
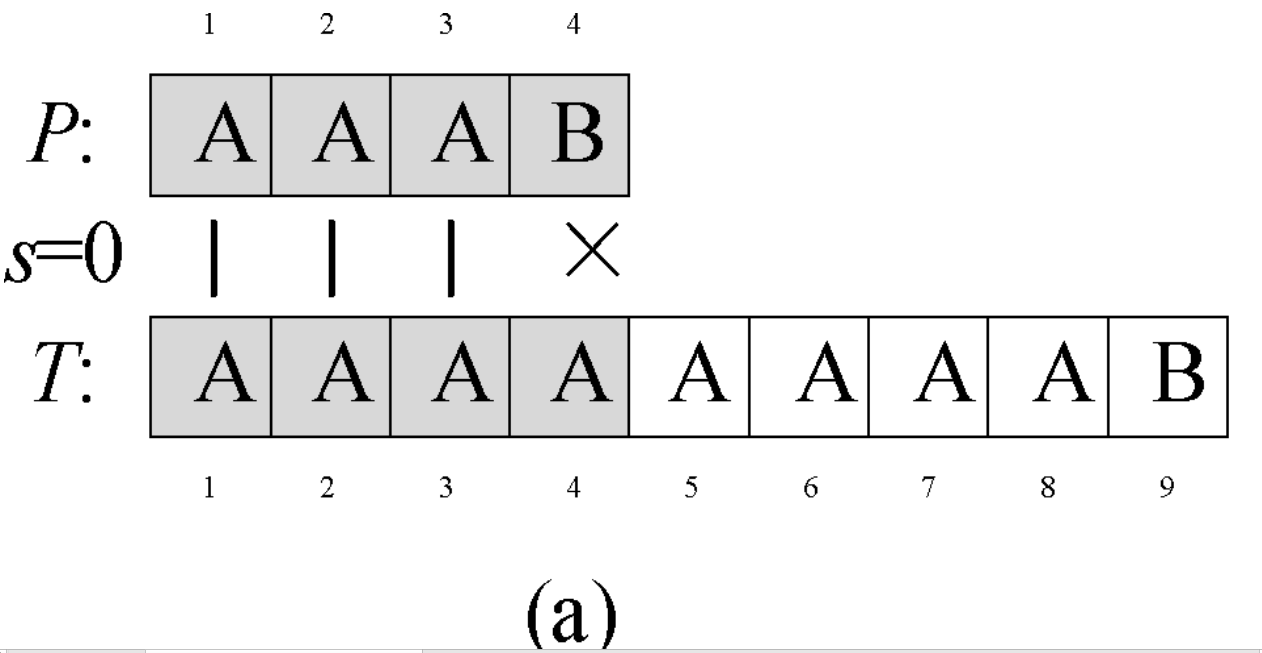
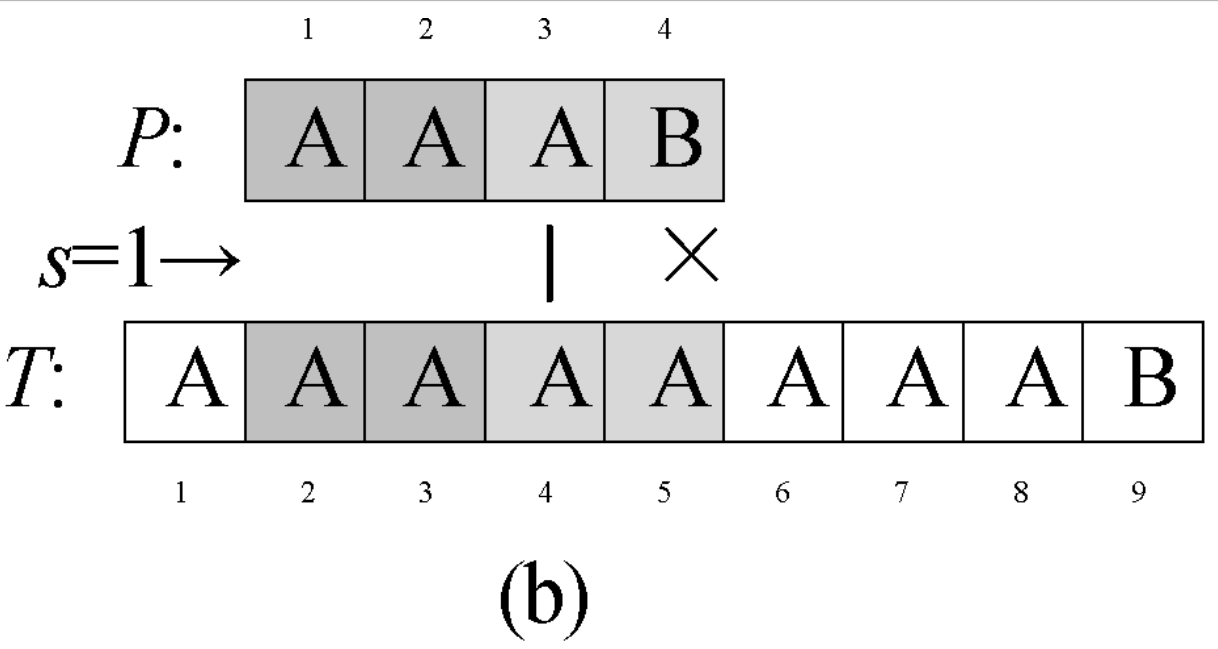
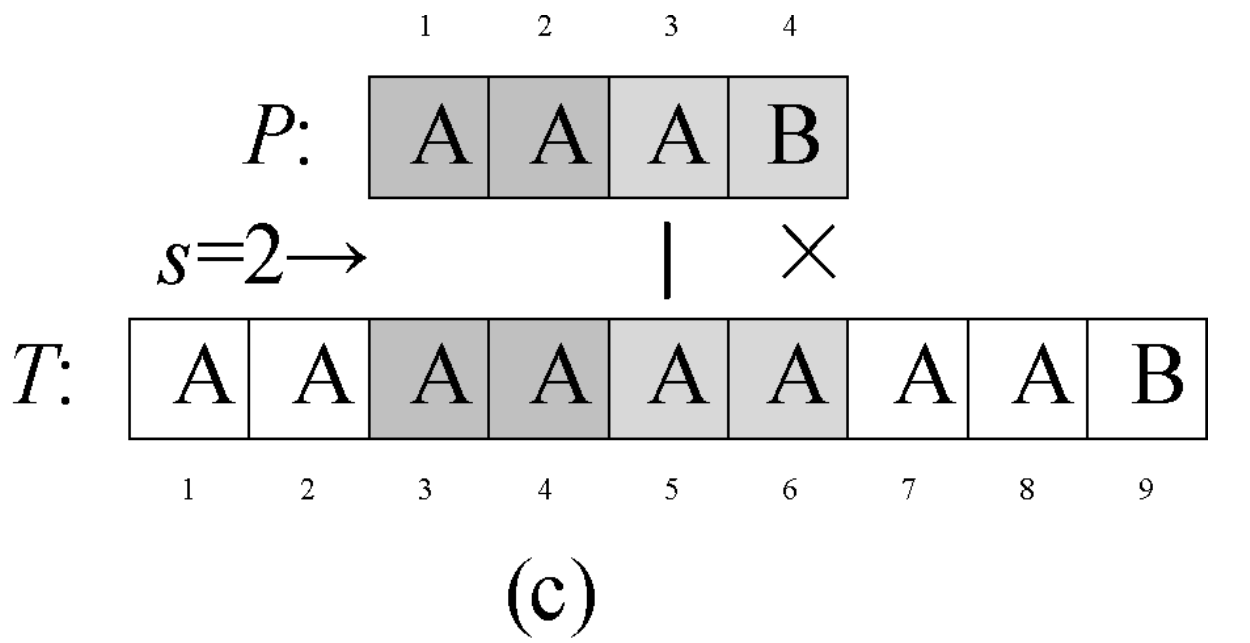
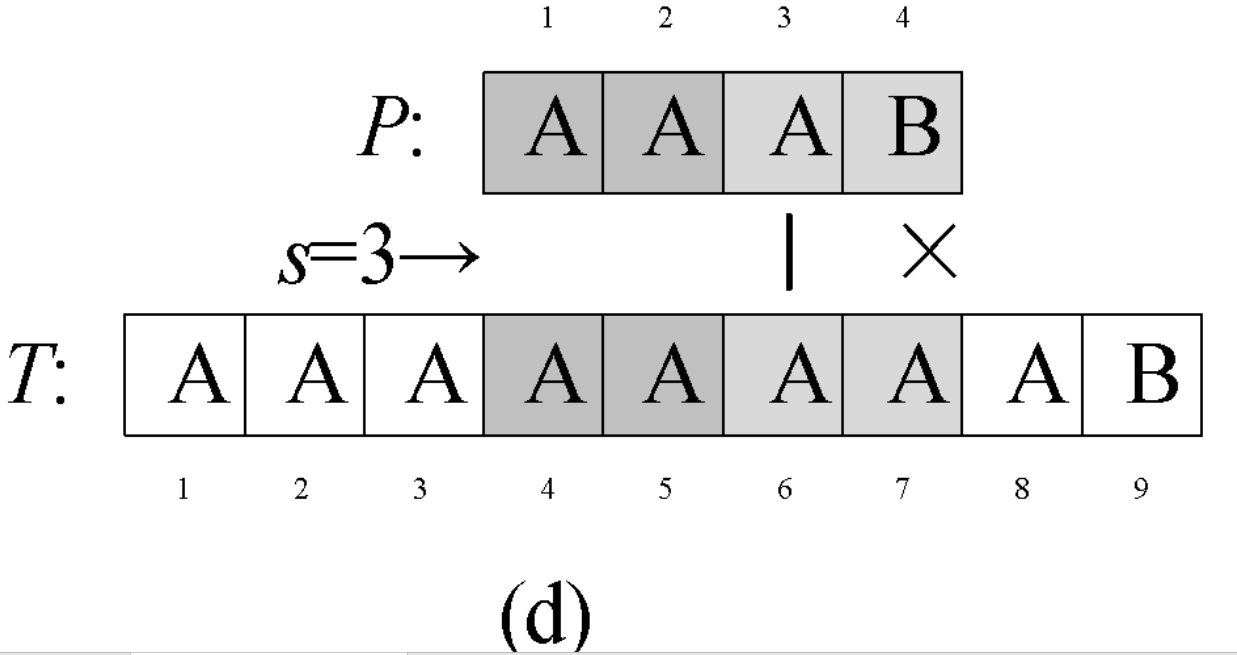
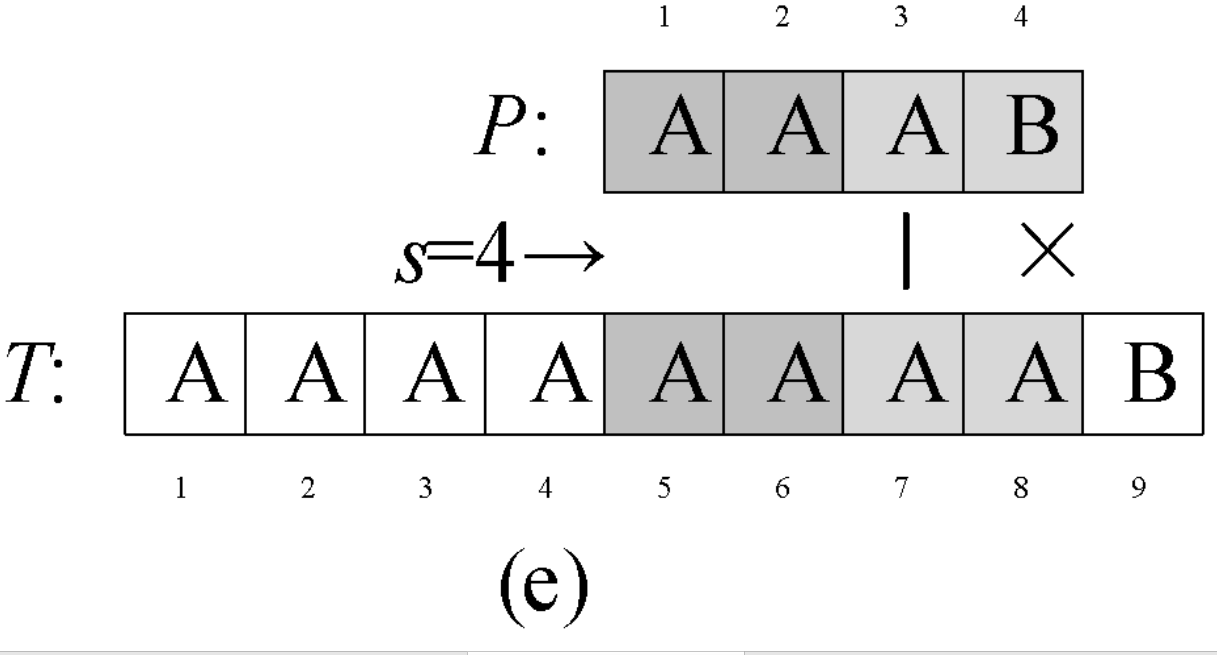
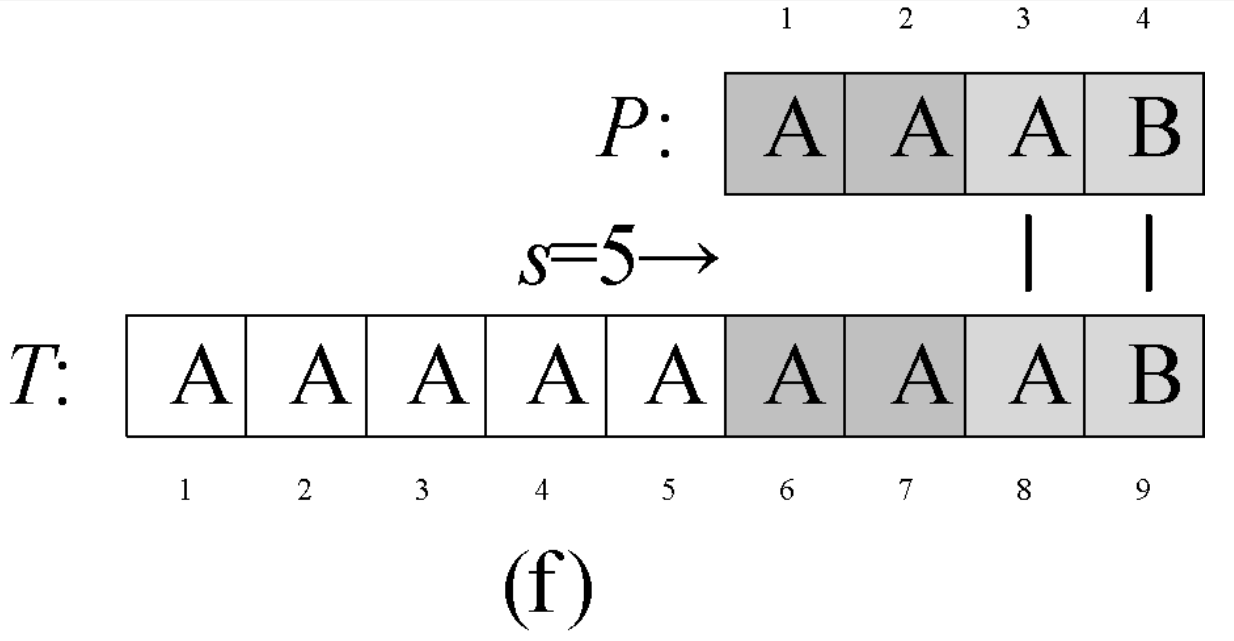
Using the structural characteristics of pattern P to accelerate the string matching process, the most famous is KMP algorithm 5 (which was independently invented by Knuth, Pratt and Morris), and its running time can be reduced from algorithm 2-9 Θ (n − m+1) reduced to linear Θ (n+m).
Question 2-6 computer viruses on Pandora
Problem description
People on Pandora have to write computer programs like us. The program they stole from the earth consists of capital letters ('A 'to' Z '). On Pandora, hackers also created some computer viruses, so Pandora people also stole virus scanning algorithms from people on earth. Each virus has A pattern string composed of uppercase letters. If the pattern string of A virus is A substring of A program, or the pattern string is A substring of the reverse string of the program, they think that the program is infected by the virus. Given A program and A series of virus pattern strings, please write A program to determine how many viruses A given program is infected with.
input
For each test case, the input contains several test cases. The first line of input is an integer T(T ≤ 10) representing the number of test cases.
The second line is an integer n representing the number of virus pattern strings (0 < n ≤ 250). Followed by N lines, each line represents a virus pattern string. Each pattern string represents a virus, and the N strings are different, so it indicates that there are n different viruses. Each mode string contains at least one character and is no longer than 1000. The last line of the test case is a string representing a program. The program may be expressed in a compressed format, which consists of uppercase letters and "compression characters". The form of the compressor is [qx], where q is an integer (0 < Q ≤ 5 000 000); And x is a capital letter. Its meaning is that there are Q consecutive letters x in the original program. For example, [6K] means "KKKK" in the original program. Therefore, if the compression program is
AB[2D]E[7K]G
The program is restored to abddekkkg.
The length of the program, whether compressed or not, is at least 1 and at most 5 100 000.
output
For each test case, an integer K representing the number of viruses infected by the program is output.
sample input
3
2
AB
DCB
DACB
3
ABC
CDE
GHI
ABCCDEFIHG
4
ABB
ACDEE
BBB
FEEE
A[2B]CD[4E]F
sample output
0
3
2
Problem solving ideas
(1) Data input and output
According to the input file format, first read the number of cases T, and then read each test case in turn. For each case, first read the number of viruses n from the input file, and then read n text lines representing viruses to form an array virus. Finally, read the text string program representing the program. For the case data virus and program, calculate the number of viruses contained in the program, and write the calculation results into the output file as a line.
Open input file inputdata Create output file outputdata from inputdata Read in T for t←1 to T do from inputdata Read in n Create array virus[1..n] for i←1 to n do from inputdata Read in virus[i] from inputdata Read in program result←COMPUTER-VIRUS-ON-PLANET-PANDORA(virus, program) take result Write as one line outputdata close inputdata close outputdata
Among them, the key to solving a test case is to call computer - virus-on-plane-pandora (virus, program) in line 10 to calculate the number of different substrings of a given length contained in a text line.
(2) The algorithmic process of handling a case
For a case data virus and program, set a counter count (initialized to 0) to successively detect whether each virus pattern virus[i] and its reverse string in are substrings of program (decompressed if necessary) (that is, whether virus[i] and its reverse string match the program string). If yes, count will increase by 1. Detect the complete array virus, and count is the required value.
COMPUTER-VIRUS-ON-PLANET-PANDORA(virus, program) n←length[virus] count←0 program1 ← EXTRACT(program) for i←1 to n do virus1←virus[i]Inverse string of if STRING-MATCHER(program 1 , virus[i])>-1 or STRING-MATCHER(program1 , virus 1 ) then count←count+1 return count
Algorithm 2-10 process of solving a case of "computer virus on Pandora"
The EXTRACT process called in the third line of the algorithm completes the decompression of the program string. The specific operations are as follows.
EXTRACT(program)
program1 ←∅, i←1
N←length[program]
while i≤N scanning program
do while i≤N and program[i]≠'[' Copy uncompressed content
do APPEND(program1, program[i])
i←i+1
if i>N
then return program
i←i+1, q←0 Compression character encountered
while program[i]As number a
do q←q*10+a
i←i+1
x←program[i]
str←q individual x Composition string
APPEND(program1, str)
i←i+1
return program1
Algorithm 2-11 algorithm process of decompressing program string
#include <iostream>
#include <fstream>
#include <string>
#include <vector>
using namespace std;
string extract(string &program)
{
string program1;
int i = 0, n = program.length();
while (i < n)
{
while (i < n && program[i] != '[')
program1 += program[i++];
if (i >= n)
return program1;
int q = 0;
i++;
while (program[i] >= '0' && program[i] <= '9')
q = q * 10 + (program[i++] - '0');
string str(q, program[i++]);
program1 += str;
i++;
}
}
int computerVirusOnPlanetPandora(vector<string> &virus, string &program)
{
int n = virus.size();
int count = 0;
string program1 = extract(program);
for (int i = 0; i < n; i++)
{
string virus1(virus[i].rbegin(), virus[i].rend());
if (program1.find(virus[i]) != string::npos ||
program1.find(virus1) != string::npos)
count++;
}
return count;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int T;
inputdata >> T;
for (int t = 0; t < T; t++)
{
int n;
inputdata >> n;
vector<string> virus(n);
for (int i = 0; i < n; i++)
inputdata >> virus[i];
string program;
inputdata >> program;
int result = computerVirusOnPlanetPandora(virus, program);
outputdata << result << endl;
cout << result << endl;
}
inputdata.close();
outputdata.close();
return 0;
}
Ordering of totally ordered set sequences
In the previous table 2-1, we listed the effects of various representations of sets on the efficiency of dictionary operations. Among them, we also gave an important operation of totally ordered sets under these representations - whether sorting is feasible or not. This is because for a fully ordered set, all elements are listed in a certain order (ascending or descending), which itself adds more useful information to the set. For example, for an ascending sequence a1,a2,..., an, we can quickly query the storage location of a specific value x element by using the "binary search" method: set q=(1+n)/2, and find such element location q if aq =x. If not, or x < a q x<a_q X < AQ, or x > a q x>a_q x>aq. For the former, according to the order of sequences a1,a2,..., an, if there is an element with value x in the sequence, it must be located in the sub sequence a1,..., AQ − 1. Similarly, if the latter occurs, X should be in aq+1,..., an. In this way, we can reduce the problem to the problem of finding X in the ordered subsequence whose length is halved. In the same way, take the intermediate value of the subsequence and compare it to determine whether it is found. If not, the scale of the problem will be further halved. In this way, the "binary search" method can find specific value elements in an ordered sequence in O(lgn) time, which will run much faster than the linear search method in the sequence introduced earlier. For the needs of science and reality, the research on sequence sequencing has a long history. For example, the "bubble sort" and the so-called "merge sort" in questions 1-8 in Chapter 1 are well-known sorting algorithms. The merging and sorting process requires an auxiliary operation - merging two ordered sequences into one ordered sequence. The idea is as follows: let L[1... N1] and R[1... n2] be ordered (ascending) sequences, and we want to merge n=n1+n2 elements in the two sequences into sequence A[1... N]. To this end, we start with the first element of L and r, compare the sizes of L[1] and R[1], and place the smaller one in A[1]. One of the remaining L or r is one element less than before comparison. Repeat the above element comparison and migration operations to obtain A[2]..., and so on, we can combine L[1... n 1] and R[1... n 2] into an ordered sequence A[1... N]. It is not difficult to see that this process is time-consuming Θ (n). If L[1... n 1]=A[p... Q] and R[1... n2] = A[q+1... r], and the above process is named MERGE(A, p, q, r), the so-called merging and sorting process of A[1... N] can be described as follows: let q=(1+n)/2, recursively do the same operation on A[1... Q] and A[q+1... N] to obtain the ordered subsequence A[p... Q] and A[q+1... r], and call MERGE(A, 1, q, n) to obtain the ordered sequence A[1... N].
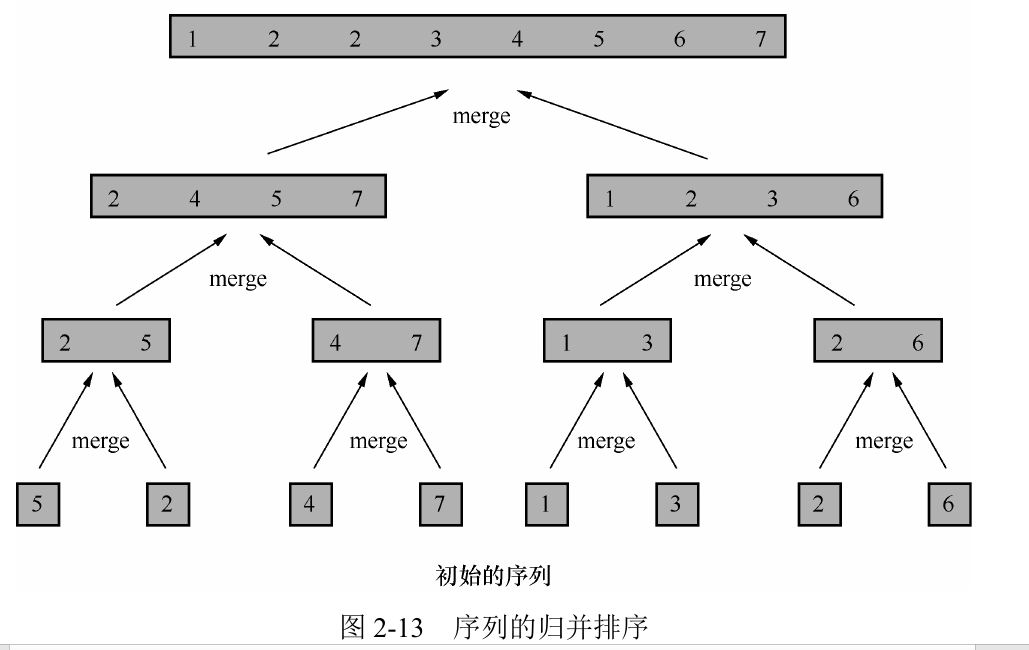
Assuming that the running time of merging and sorting of A[1... N] is T(n), the merging and sorting of A[p... q] and A[q+1... r] takes T(n/2) respectively, plus the time of increasing MERGE(A, 1, q, n) Θ (n) , we get
T
(
n
)
=
2
T
(
n
/
2
)
+
Θ
(
n
)
T(n)=2T(n/2)+Θ(n)
T(n)=2T(n/2)+Θ(n)
In the above formula, the Θ (n) Simplification to n does not affect the asymptotic representation of T(n). That is, the above formula can be expressed as
T
(
n
)
=
2
T
(
n
/
2
)
+
n
T(n)=2T(n/2)+n
T(n)=2T(n/2)+n
Θ ( n l g n ) Θ(nlgn) Θ (nlgn) the running time of bubble sort is Θ (n2)
Question 2-7 DNA sequencing
Problem description
One way to measure the "clutter" of a sequence is to count the logarithms of elements in the sequence that do not conform to the order from small to large. For example, in this way, the measure of the alphabetic sequence "DAABEC" is 5. Because D is larger than the four letters on its right, and E is larger than the one letter on its right. This measure is called the inverse number of sequences. The sequence "AACEDGG" has only one reverse order (E and D) - it is almost well ordered. The sequence "ZWQM" has 6 reverse orders (this is the most "messy" sequence - reverse sequence).
Please sort a sequence composed of a DNA string (the string contains only four letters A,C,G and T). Sorting rules are not in dictionary order, but in the order of their reverse number from small to large.
input
The first line of the input file contains two integers n (0 < n ≤ 50) and m (0 < m ≤ 100), representing the length and number of strings respectively. The following M lines represent m DNA strings of length n.
output
The m strings in the input file are output to the output file in the order of inverse ordinal number from small to large, and each line is output to the output file.
sample input
10 6
AACATGAAGG
TTTTGGCCAA
TTTGGCCAAA
GATCAGATTT
CCCGGGGGGA
ATCGATGCAT
sample output
CCCGGGGGGA
AACATGAAGG
GATCAGATTT
ATCGATGCAT
TTTTGGCCAA
TTTGGCCAAA
(1) Data input and output
According to the input file format, first read n and m representing the string length and the number of strings from the input file. Then read m rows, one string per row, and organize them into an array DNAS[1... m]. DNAS is sorted in ascending order according to the reverse number of each string. Write one string per line of the ordered DNAS into the output file.
Open input file inputdata Create output file outputdata from inputdata Read in n and m for i←1 to m do Create array DNAS[1..m] from inputdata Read a line from to DNAS[i] DNA-SORTING(DNAS) for i←1 to m do take DNAS[i]Write as one line outpudata close inputdata close outputdata
Among them, the key to solve this problem is the process DNA-SORTING(DNAS) called in line 7 to calculate the reverse order number of each string in DNAS and sort DNAS according to the ascending order of the reverse order number.
(2) The algorithmic process of handling a case
First, we need an algorithm to calculate the reverse order number of DNA string composed of four symbols (A,C,G,T). Set a counter count (initialized to 0) and scan the string in reverse order. The ith element dna[i] calculates the number of elements greater than it before it and adds it to the count. After scanning, the obtained count is the required value. In order to calculate the number of elements larger than dna[i], we set a counter for symbols C, G and T C C , C G , C T C_C,C_G,C_T CC, CG and CT (all initialized to 0), which respectively track the number of C, G and T before the ith element. For dna[i], if
INVERSION(dna) n←length[dna], count←0 cC←0,cG←0,cT←0 for i←1 to n do if dna[i]= "A" then count←count+(cC + cG + cT) else if dna[i]= "C" then count←count+(cG + cT) cC←cC+1 else if dna[i]= "G" then count←count+ cT cG ← cG +1 else cT ← cT +1 return count
The running time of this algorithm depends on the number of repetitions n of the for loop in lines 3 ~ 13. Each time, the operation in the circulatory body takes Θ (1). So the running time of the algorithm is Θ (n).
Using the INVERSION process, we solve the DNA sequencing problem. Create a temporary sequence a, and add the binary (dna, inv) composed of each string in DNAS[1... m] and its inverse number inv to a. Then, a is sorted in ascending order according to the inv attribute of the elements, and the DNA attributes of the elements in a are copied back to DNAS in turn. The specific process is written as pseudo code as follows.
DNA-SORTING(DNAS)m ←length[DNAS]Create collection afor i←l to m do inv[DNAS [i]]←INVERSION(string[DNAS [i]])SORT(DNAS
cpp
#include <fstream>
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <iterator>
using namespace std;
int inversion(const string &dna)
{
int count=0,n=dna.length();
int cC=0, cG=0, cT=0;
for(int i = 0;i < n;i++)
{
switch(dna[i])
{
case 'A':count+=(cC+cG+cT);
break;
case 'C':count+=(cG+cT);
cC++;
break;
case 'G': count+=cT;
cG++;
break;
default:cT++;
}
}
return count;
}
struct Dna:public string
{
int inv;
Dna(string s="",int i=0):string(s),inv(i){}
};
bool operator<(const Dna &a,const Dna &b)
{
return a.inv < b.inv;
}
void dnaSorting(vector<Dna> &dnas)
{
int m = dnas.size();
for(int i = 0;i < m;i++)
{
dnas[i].inv = inversion(dnas[i]);
}
sort(dnas.begin(),dnas.end());
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int n,m;
inputdata >> n>>m;
vector<Dna> dnas;
for(int i = 0;i < m;i++)
{
Dna s;
inputdata>>s;
dnas.push_back(s);
}
dnaSorting(dnas);
copy(dnas.begin(), dnas.end(), ostream_iterator<string>(outputdata, "\n"));
copy(dnas.begin(), dnas.end(), ostream_iterator<string>(cout, "\n"));
inputdata.close();
outputdata.close();
return 0;
}
Question 2-8 degrees bear's gift
Problem description
Dudu bear has its own Baidu space. Dudu bear will give gifts to space friends from time to time to increase the friendship value between Dudu bear and his friends. Dudu bear got two kinds of super gifts by chance, so he decided to give each friend a super gift. Different types of friends can achieve different happiness values when receiving different gifts. The measurement standard of happiness value is as follows: each super gift has two attributes (A, B), and each friend also has two attributes (X, Y). If the friend receives the super gift, the happiness value obtained by the friend is AX+BY. Due to the limited number of super gifts, Dudu bear is curious: how to distribute these gifts to maximize the total happiness of his friends?
input
The first line n represents the number of friends of the Dudu bear.
Next n lines, two integers in each line represent the two attributes Xi and Yi of Du Xiong's good friend.
The next two lines are three integers ki,Ai and Bi in each line, indicating the number and attribute value of the i-th super gift. 1 ≤ n ≤ 1000,0 ≤ Xi,Yi,Ai,Bi ≤ 1000,0 ≤ ki ≤ n, ensure k1+k2 ≥ n.
output
Output a value in one line, which represents the maximum value of the sum of friends' happy values.
sample input
4
3 6
7 4
1 5
2 4
3 3 4
3 4 3
sample output
118
Problem solving ideas
(1) Data input and output
According to the description of the input file format, first read the number of friends n from the input file, then read the attribute data of n friends and organize them into two arrays X[1... N] and Y[1... N]. Finally, read the attributes and number of two gifts from the input file: A1,B1,k1 and A2,B2,k2. For the input data, calculate the gift distribution to all friends and the total number of maximum happiness values of friends. Write the result as a line to the output file.
Open input file inputdata Create output file outputdata from inputdata Read in n Create array X[1..n]and Y[1..n] for i←1 to n do from inputdata Read in X[i]and Y[i] from inputdata Read in k1,A1,B1 from inputdata Read in k2,A2,B2 result←GIFTS(X, Y, k1, A1, B1, k2, A2, B2) take result Write as one line outputdata close inputdata close outputdata
Among them, line 9 calls the process gifts (x, y, A1, B1, K1, A2, B2, K2) to calculate the maximum happy value of friends, which is the key to solve the problem.
Since the i-th friend's happiness with both gifts can be calculated, they are A iX1+BiY1 and AiX2+BiY (i=1,2,..., n). You can decide the type of gift for the ith friend according to the size of these two values. Two sets S1 and S2 can be maintained. The former stores the friend number given to the first gift and the happy value of the gift obtained by the friend, and the latter stores the same information given to the friend of the second gift. If the number of elements n1 of S1 exceeds k1, the numbers of n1 − k1 friends with the lowest happy value and their happy value of accepting the second gift are transferred to S2. If the number of elements n2 of S2 exceeds k2, do the same for S2. Finally, the sum of the open center values of the elements in S1 and the sum of the open center values of the elements in S2 is the result.
GIFTS(X, Y, k1, A1, B1, k2, A2, B2) n←length[X] S1←∅, S2←∅ for i←1 to n do if A1X[i]+B1Y[i]>A2X[i]+B2Y[i] then INSERT(S1, <A1X[i]+B1Y[i], i>) INSERT(S2, <A2X[i]+B2Y[i], i>) n1←length[S1], n2←length[S2] if n1>k1 then SORT(S1) take S1 At the end of n1-k1 Remove the elements and add the second value corresponding to these elements S2 else if n2>k then SORT(S2) take S2 At the end of n2-k2 Remove the first element and add the corresponding value of the first gift S1 return S1 Sum of happy values in+S2 Sum of happy values in
Algorithm 2-14 process of solving the "gift of the bear" problem
If the sum is represented as a linear table (array) and the newly added element is placed at the end, the for loop in lines 3 ~ 6 takes time Θ (n). The call to SORT the linear table in rows 8 ~ 13 is executed at most once, which is theoretically time-consuming Θ (nlgn). Line 14 needs to calculate the sum of elements in S1 and S2, which takes time Θ (n). Therefore, the algorithm is time-consuming at most Θ (nlgn).
#include <iostream>
#include <fstream>
#include <vector>
#include <algorithm>
using namespace std;
struct Gift
{
int value,index;
Gift(int v,value)b.value(v),index(i){};
};
bool operator>(const Gift &a, const Gift &b)
{
return a.value > b.value;
}
int gifts(vector<int> &X,vector<int> &Y,int k1,int A1, int B1, int k2, int A2, int B2)
{
int sum = 0;
int n=X.size();
vector<Gift>S1,S2;
for(int i = 0;i < n; i++)
{
int v1=A1*X[i]+B1*Y[i], v2=A2*X[i]+B2*Y[i];
v1>v2?S1.push_back(Gift(v1,i)):S2.push_back(Gift(v2, i))
}
int n1=S1.size(),n2=S2.size();
if(n1>k1)
{
sort(S1.begin(), S1.end(), greater<Gift>());
for(int i = 0;i<n1-k2,i++)
{
S2.push_back(Gift(A2*X[S1[k1+i].index]+B2*Y[S1[k1+i].index], 0));
n2++;
}
S1.erase(S1.begin()+k1, S1.end());
n1-=k1;
}
else if(n2>k2)
{
sort(S2.begin(),S2.end(),greater<Gift>());
for(int i = 0;i<n2-k2;i++)
{
S1.push_back(Gift(A1*X[S2[k2+i].index]+B1*Y[S2[k2+i].index], 0));
n1++;
}
S2.erase(S2.begin()+k2,S1.end());
n2-=k2;
}
for(int i = 0;i<n1;i++)
sum+=S1[i].value;
for(int i=0;i<n2;i++)
sum+=S2[i].value;
return sum;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int n;
inputdata>>n;
vector<int>X,Y;
for(int i =0;i<n;i++)
{
int x,y;
inputdata>>x>>y;
X.push_back(x);
Y.push_back(y);
}
int A1, B1, k1, A2, B2, k2;
inputdata>>k1>>A1>>B1;
inputdata>>k2>>A2>>B2;
int result=gifts(X, Y, k1, A1, B1,k2, A2, B2);
outputdata<<result<<endl;
cout<<result<<endl;
inputdata.close();
outputdata.close();
return 0;
}
Question 2-9 communication system
Problem description
We have just received an order from pizoo communications for a special system. The system consists of several devices. We can choose from several manufacturers for each kind of equipment. For the same equipment, the maximum bandwidth and price of different manufacturers are different. The minimum bandwidth of all equipment in the system is called the global bandwidth (B), and the sum of the prices of the selected equipment constituting the communication system is called the total price §. Our goal is to select a manufacturer for each device to maximize B/P.
input
The first line of the input file contains an integer T (1 ≤ T ≤ 10), representing the number of cases. Then enter the data of each case. The first line of each case contains an integer n (1 ≤ n ≤ 100), which represents the number of devices in the communication system, followed by N lines of data of each device. Each line starts with mi representing the number of manufacturers, followed by mi pairs, which represent positive integers of bandwidth and price of devices provided by each manufacturer.
output
Your program generates and outputs a line for each input case, containing only one data representing the maximum possible B/P, which is rounded to 3 decimal places.
sample input
1
3
3 100 25 150 35 80 25
2 120 80 155 40
2 100 100 120 110
sample output
0.649
Problem solving ideas
(1) Data input and output
According to the input file format, first read the number of cases t, and then read the data of each case in turn. The first line of the case only contains n indicating the number of devices, and the integer m at the beginning of each line of the subsequent n lines represents the number of providers of a device, and then the mi pair represents the bandwidth b and price p of the device provided by a merchant. Organize the supply data of N devices into nested arrays: devices[1... N], where devices[i] is an array with mi elements d e v i c e s [ i ] [ 1.. m i ] devices[i][1..m_i] devices[i][1..mi] each of its elements d e v i c e s [ i ] [ j ] devices[i][j] devices[i][j] is a binary (b, p) representing the bandwidth and price given by the j-th supplier of the i-th device. Write all product ratios B/P and the calculated results with an accuracy of 3 decimal places into the output file as one line.
Open input file inputdata Create output file outputdata from inputdata Read in T for t←1 to T do from inputdata Read in n Create array devices[1..n],And for each k,establish devices[k]←∅ Create collection bands←∅ for i←1 to n do from inputdata Read in mi for j←1 to mi do from inputdata Read in(b, p) INSERT(devices[i], (b, p)) INSERT(bands, b) result←COMMUNICATION-SYSTEM(devices, bands) take result Write in one line with the precision of three decimal places outputdata close inputdata close outputdata
Among them, line 14 calls the process communication system (devices, bands) to calculate and configure the maximum cost performance of all devices, which is the key to solving a test case.
(2) The algorithmic process of handling a case
For the data devices and bands of a case, the goal is to calculate the maximum B/P, where B is the minimum bandwidth in the selected device and P is the sum of the selected prices. Therefore, we investigate each value B in bands, which can play the role of B in the optimal solution. For each device, there must be at least one supplier whose device bandwidth B ≥ B. For specific B, it is also necessary to consider making the total price P of the selected equipment smaller. This can be achieved by selecting the minimum price P of each equipment on the premise that B meets the requirements (B ≥ B). In order to quickly select the appropriate device constraint (b, p) in devices[i], we can sort devices[i] according to the descending order of B attribute in advance, check whether B of (b, p) ∈ devices[i] is not less than B from scratch, select a smaller pmin from the devices that meet this condition and add it to P.. Once b > b is detected, you can immediately stop the search in devices[i] (if devices[i] is not sorted, you need to conduct a full search). If there is no device with bandwidth B not less than B in devices[i], discard this B and detect the next element in bands. In order to improve the scanning efficiency, track the P determined according to the above method for the element B of bands, and the maximum B/P is the required value. The above algorithm idea is written into pseudo code, and the process is as follows.
COMMUNICATION-SYSTEM(devices, bands)
n←length[devices], r←0
for i←1 to n
do SORT(devices[i])
for each B∈bands Examine each possible bandwidth
do P←0
for i←1 to n Inspect each equipment
do pmin←∞
for each (b, p) ∈devices[i]On the first i The bandwidth of each device shall not be less than B Vendor data for
do if b<B from devices[i]Descending order of,There is no need to consider the following data
then break this loop
if p<pmin Track the minimum price that meets the criteria
then pmin←p
if pmin=∞ No compliance, bandwidth not less than B Equipment under this condition
then break this loop
P←P+pmi
if i≤n No compliance, bandwidth not less than B Equipment under this condition
if r<B/P
then r←B/P
return r
Algorithm 2-15 algorithm process of solving a case of "communication system" problem
In the algorithm, lines 2 to 3 sort each device [i] (1 ≤ I ≤ n) according to the descending order of the b attribute of the element, taking Ω (n2lgn). Suppose m=max{m1, m2,..., mn}, in the triple nested loop of lines 4 ~ 19, the first layer repeats O(nm), the second layer repeats n times, and the third layer repeats O(m). Thus, the running time of the algorithm is O(n2m2).
#include <iostream>
#include <fstream>
#include <vector>
#include <set>
#include <algorithm>
#include <climits>
using namespace std;
struct Device
{
int b, p;
Device(int x, int y): b(x), p(y) {}
};
bool operator>(const Device &a, const Device &b)
{
return a.b > b.b;
}
double communicationSystem(vector<vector<Device>> &devices, set<int> bands)
{
double r = 0.0;
int n = devices.size();
for (int i = 0; i < n; i++)
sort(devices[i].begin(), devices[i].end(), greater<Device>());
for (set<int>::iterator i = bands.begin(); i != bands.end(); i++)
{
int B = *i, P = 0, k;
for (k = 0; k < n; k++)
{
int temp = INT_MAX;
for (int j = 0; j < devices[k].size(); j++)
{
if (devices[k][j].b < B)
break;
if (devices[k][j].p < temp)
temp = devices[k][j].p;
}
if (temp == INT_MAX)
break;
P += temp;
}
if (k < n)
continue;
double r1 = double(B) / double(P);
if (r1 > r)
r = r1;
}
return r;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int T;
inputdata >> T;
for (int t = 0; t < T; t++)
{
int N;
inputdata >> N;
vector<vector<Device>> devices(N, vector<Device>());
set<int>bands;
for (int i = 0; i < N; i++)
{
int mi;
inputdata >> mi;
for (int j = 0; j < mi; j++)
{
int b, p;
inputdata >> b >> p;
devices[i].push_back(Device(b, p));
bands.insert(b);
}
}
}
}
Union, intersection and difference of sets
In many application problems, union, intersection and difference operations between homogeneous sets (with the same element types in the set) will also be involved. Implementing these operations usually requires scanning the elements of the collection.
INTERSECTION(A, B) aggregate A And B Hand in C←∅ for each x∈A do if x∈B then INSERT(C, x) return C
DIFFERENCE(A, B) aggregate A And B Poor C←∅, T←INTERSECTION(A, B) for each x∈A do if x∉T then INSERT(C, x) return C
UNIN(A, B) aggregate A And B And T←INTERSECTION(A, B) , C←DIFFERENCE(B, T) for each x∈A do INSERT(C, x) return C
Algorithm 2-16
Calculate the algorithm process of set merging, intersection and difference
Obviously, each operation process needs to scan, query and insert the collection. The different representations of the collection in the computer will also affect the efficiency of these operations of the collection. If the set is represented as A linear table, and assuming that the number of elements of A and B is equal (set to n), the running time to realize these three algorithms is Θ (n 2).
Problem 2-10 computer scheduling
Problem description
As we all know, computer scheduling is a classical problem in computer science, and the research on this problem has a long history. The machine scheduling problem is different from the scheduling problem under constraints. Here we consider the 2-machine scheduling problem
There are two computers A and B. Machine A has N working modes, which are recorded as mode_0,mode_1, …, mode_n−1. Similarly, machine B has m working modes, which are recorded as mode_0,mode_1,…,mode_m−1. They always start from mode_0 started working. There are k tasks, each of which can be processed in A specific mode of two machines. For example, job 0 can be in the mode of machine A_ Mode of machine 3 or B_ 4. job 1 can be processed in the mode of machine A_ Mode of machine 2 or B_ 4 processing, etc. Therefore, job i and its constraints can be expressed as triples (i, x, y), which means that it can be in the mode of machine A_ Mode of X or B machine_ Y processing. Obviously, to complete the processing of all tasks, it is necessary to change the working mode of the computer from time to time. Unfortunately, when A computer changes from one mode to another, it must be turned off and then turned on before switching. Write A program to minimize the number of computer restarts by changing the processing order of tasks and specifying the appropriate machine for the task.
input
The input file contains several test cases. The first line of each case contains three integers: n, m (n, m < 100) and K (k < 1000). Then, K rows give the constraints of K tasks, and each row is represented as a triple: i,x,y. The input file ends with a line of data containing only 0.
output
Each case output line contains an integer representing the minimum number of machine restarts.
sample input
5 5 10
0 0 0
1 0 1
2 0 2
3 0 3
4 1 0
5 1 1
6 1 2
7 1 3
8 2 2
9 3 2
0
sample output
3
Problem solving ideas
(1) Data input and output
According to the format description of the input file, the first data of each case is n representing the mode number of machine A, and N = 0 is the end flag of the input file. For each case where n > 0, m and K representing the number of modes and tasks of machine B need to be read next. Next is k sets of data (i,x,y) describing each task constraint. Organize this K group of data into three arrays i[1... k],x[1... K] and y[1... K]. For the case data n, m, I, X and y, calculate the minimum startup times for completing all tasks, and write the calculated results into the output file as one line. Until n read from the input file is 0.
Open input file inputdata Create output file outputdata from inputdata Read in n while n≠0 do from inputdata Read in m and k Create array i[1..k],x[1..k],y[1..k] for j←1 to k do from inputdata Read in i[j],x[j],y[j] result←MACHINE-SCHEDULE(n,m,i,x,y) take result Write as one line outputdata from inputdata Read in n close inputdata close outputdata
Line 9 calls the process MACHINE-SCHEDULE(n) to calculate the minimum boot times required to complete all tasks,
m. I, x, y) is the key to solve a test case.
(2) In the algorithm process of processing A case, n+m modes are expressed as n+m sets, which are organized into an array mode[0... n+m − 1]:A machine mode_0,mode_1, …, mode_n − 1 is mode[0... N − 1], and B machine mode is mode_0,mode_1, …, mode_m − 1 is mode[n... n+m − 1]. Add the constraint data (i, x, y) of each task in the input to the set mode[x] and mode[n+y] according to its running mode. For example, the input examples can be expressed as: mode[0]={0,1,2,3},mode[1]={4,5,6,7},mode[2]={8},mode[3]={9},mode[4] = ∅, mode[5]={0,4},mode[6]={1,5},mode[7]={2,6,8,9},mode[8]={3,7},mode[9] = ∅. To solve this problem, we adopt the following "greedy" strategy: select the mode that can run the most tasks each time. In this way, all tasks can be completed after starting the machine at least once. For example, in the input sample, all tasks are {0,1,..., 9}. First, select the task set to be run as mode[0]={0,1,2,3}, its cardinality is 4 (one of the largest), and it conforms to the mode in which A starts up for the first time. Record the boot times as 1. After {0,1,2,3} (meaning running these tasks) is removed from all modes, the status of each mode is: mode[0] = ∅, mode[1]={4,5,6,7}, mode[2]={8}, mode[3]={9}, mode[4] = ∅, mode[5]={4},mode[6]={5},mode[7]={6,8,9},mode[8]={7},mode[9] = ∅. Tasks that are not currently running become {4, 5, 6, 7, 8, 9}. Then select the task set to be run as mode[1]={4,5,6,7}, the base number is 4 (the largest), and the number of boot times increases by 1 to 2. Run task {4,5,6,7}, then the status of all modes is: mode[0] = ∅, mode[1] = ∅, mode[2]={8}, mode[3]={9}, mode[4] = ∅, mode[5] = ∅, mode[6] = ∅, mode[7]={8,9},mode[8] = ∅, mode[9] = ∅. The remaining tasks are {8,9}. Select the mode with the largest base, mode[7]={8,9}, as the task to be run. When running, the number of boot times increases to 3. Complete the operation of all tasks after removing {8,9} in each mode. The required number of starts is 3. Generally, set the task set jobs that have not been run at present and initialize them as all tasks {0,1,..., n+m − 1}. Set the task set currently ready to run as R. since the two machines are always in mode[0] and mode[n] for the first time, R is initialized to the greater of mode[0] and mode[n]. Set A counter num to track the number of boot times and initialize it to 0. Each time, remove the tasks in R from all modes, remove r from jobs (which means that these tasks have completed running), and increase num by 1 (which means that A boot is added). Set R to the one with the largest cardinality in the current modes and prepare for the next boot. Cycle until jobs is empty. The process of writing pseudo code is as follows.
MACHINE-SCHEDULE(n,m,i,x,y)
Create array mode[0..n+m-1]←{∅, ∅, ..., ∅}
k←length[x], jobs←∅
for j←0 to k-1
do INSERT(mode[x[j]], i[j])
INSERT(mode[n+y[j]], i[j])
INSERT(jobs, j)
R←mode[0],mode[n]Whichever is larger
num←0
while jobs≠∅
do num←num+1
jobs←jobs-R
for j←0 to n+m-1
do mode[j]←mode[j]-R
R←mode[0..n+m-1]The one with the largest base
return num
#include <iostream>
#include <fstream>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;
bool operator<(const set<int> &a, const set<int> &b)
{
return a.size() < b.size();
}
class Comp
{
public:
bool operator()(set<int> &a, set<int> &b)
{
return a < b;
}
};
int machineSchedule(int n, int m, vector<int> &i, vector<int> &x, vector<int> &y)
{
vector<set<int>> mode(n + m, set<int>());
set<int> jobs;//Unprocessed task collection
int k = x.size();
for (int j = 0; j < k; j++)
{
mode[x[j]].insert(i[j]);//Record the working mode of machine A for task i
mode[n + y[j]].insert(i[j]); //B machine working mode of recording task i
jobs.insert(j);
}
set<int> r = mode[0].size() > mode[n + m - 1].size() ? mode[0] : mode[n + m - 1]; //Tasks to be processed on the first boot
int num = 0; //Machine restart times
while (!jobs.empty()) //There are still outstanding tasks
{
num++;
int *temp = new int[jobs.size()];
int *p = set_difference(jobs.begin(), jobs.end(), r.begin(), r.end(), temp); //Handle this task
jobs = set<int>(temp, p);
delete []temp;
for (int j = 0; j < n + m; j++) //Adjust the acceptable tasks of each mode
{
temp = new int[mode[j].size()];
p = set_difference(mode[j].begin(), mode[j].end(), r.begin(), r.end(), temp);
mode[j] = set<int>(temp, p);
delete []temp;
}
int j = distance(mode.begin(), max_element(mode.begin(), mode.end(), Comp())); //Mode that can handle the most tasks
r = mode[j]; //Tasks to be processed next time
}
return num;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int n;
inputdata >> n;
while (n > 0)
{
int m, k;
inputdata >> m >> k;
vector<int> i(k), x(k), y(k);
for (int j = 0; j < k; j++)
inputdata >> i[j] >> x[j] >> y[j];
int result = machineSchedule(n, m, i, x, y);
outputdata << result << endl;
cout << result << endl;
inputdata >> n;
}
inputdata.close();
outputdata.close();
return 0;
}
Question 3-1 symmetric sorting
Problem description
You work for the albatross circus with a group of ugly stars as the pillars. You have just completed a program that outputs their list in non descending order according to the length of the stars' name string (that is, the length of the current name is at least the same as that of the previous name). However, your boss doesn't like this output format. He proposes that the length of the first and last names of the output is short, while the length of the middle part is slightly longer, which appears symmetrical. The specific method mentioned by the boss is to deal with the list that has been sorted by length one by one, putting the former at the head of the current sequence and the latter at the tail. For the first case in the input example, Bo and Pat are the first pair of names, Jean and Kevin are the second pair, and so on.
input
The input contains several test cases. The first line of each case contains an integer n(n ≥ 1), indicating the number of name strings. The next N lines each line a name string, which is arranged by length. The name string does not contain spaces, and each string contains at least one character. n=0 is the end of input flag.
output
For each test case, first output a line of "SET n", where n starts from 1, indicating the case serial number. Next is the n-line name output, as shown in the output example.
sample input
7
Bo
Pat
Jean
Kevin
Claude
William
Marybeth
6
Jim
Ben
Zoe
Joey
Frederick
Annabelle
5
John
Bill
Fran
Stan
Cece
0
sample output
SET 1
Bo
Jean
Claude
Marybeth
William
Kevin
Pat
SET 2
Jim
Zoe
Frederick
Annabelle
Joey
Ben
SET 3
John
Fran
Cece
Stan
Bill
Problem solving ideas
(1) Data input and output
According to the input file format, read the integer n in the first line of each test case, and then read the list of N clowns in the case in order by length, and organize them into a sequence names. Rearrange the name strings in names according to the boss's opinion, and then write them to the output file one by one. Case data n=0 is the end flag of the input file.
Open input file inputdata Create output file outputdata from inputdata Read in n num←1 while n>0 do Create sequence names←∅ for i←1 to n do from inputdata Read a line from to name INSERT(names, name) SYMMETRIC-ORDER(names) take"SET num"Write as one line outputdata for each name in names do take name Write as one line outputdata from inputdata Read in n close inputdata close outpudata
Among them, line 10 calls the process of rearranging the list names according to the boss's opinion. Geometric-order (names) is the key to solving a case.
(2) The algorithmic process of handling a case
For the list names stored in the sequence in ascending order of length, to rearrange according to the boss's opinion, we need to set two position pointers I and j for names, which are initialized to 2 and n+1 respectively. Move names[i] before names[j], and I increases by 1 and j decreases by 1. Repeat this operation until I > ⎣ n/2 ⎦ 1(n is an even number) or I > ⎣ n/2 ⎦ + 1(n is an odd number). For example, for the data of case 1 in the input sample, the rearrangement process is shown in Figure 3-1.
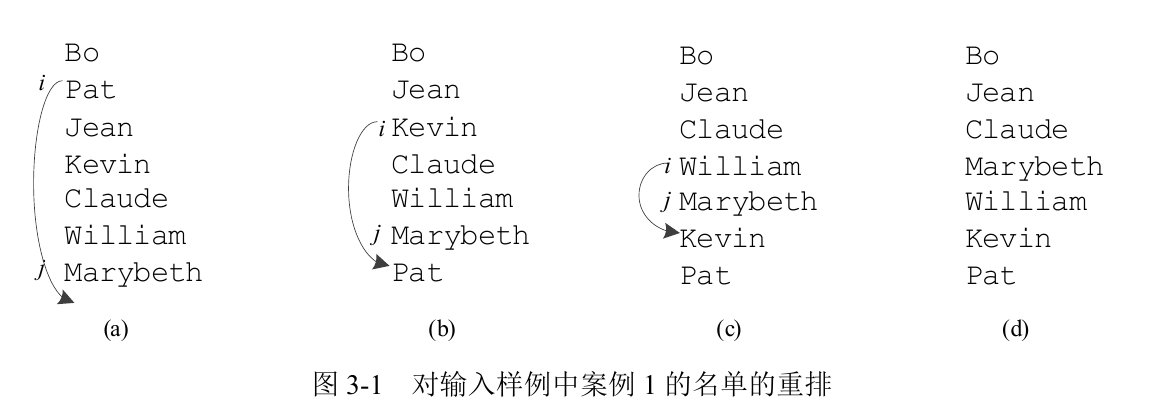
In case 1 in the input example, there are n=7 names in the list. Figure 3-1(a) shows the initial state of, I is 2,j is 8(=n+1). Move Pat(=names[i]) after Marybeth (before names[j]), as shown by the arrow arc in Figure 3-1(a), and I increases by 1 to 3 and j decreases by 1 to 7 to obtain the state shown in Figure 3-1(b). Repeat the operation of moving names[i] before names[j] for state (b), and I increases by 1 and j decreases by 1 to obtain the state © . At this time, i=4=3+1 = ⎣ n/2 ⎦ + 1 reaches the critical point. Insert names[i] before names[j] for the last time, and I increases by 1 and j decreases by 1 to reach the final state (d). Such a simulated rearrangement process is represented as the pseudo code for processing the list in general, as follows.
SYMMETRIC-ORDER(names) n←length[names] if n Even number then m←⎣n/2⎦ else m←⎣n/2⎦+1 i←2, j←n+1 while i≤m do name←names[i] take name Insert into names[j]before DELETE(names, name) i←i+1, j←j-1
Algorithm 3-1 algorithm process of a case to solve the "symmetric sorting" problem
The running time of the algorithm depends on the number of while loop repetitions in lines 6 to 10. Obviously, the loop repeats m= Θ (n/2)= Θ (n) Times. In addition to the constant time operations in lines 7 and 10, the elements are inserted in the sequence names in line 8 and deleted in line 9. If you represent names as an array, you can see from table 2-1 that both operations will take time Θ (n). Thus, the running time of algorithm 3-1 is Θ (n2). If names is represented as a linked list, it is known from table 2-1 that it takes time to insert and delete elements Θ (1). Thus, the running time of algorithm 3-1 is Θ (n)
#include <iostream>
#include <fstream>
#include <list>
#include <string>
#include <iterator>
using namespace std;
void symmetricOrder(list<string> &names)
{
int n = names.size();
int m = (n%2==1)?(n/2+1):n/2;
int k = 1;
list<string>::iterator i = ++(names.begin()),j = (names.end());
while(k<m)
{
names.insert(j,*i);
names.erase(i++);
i++;j--;
k++;
}
}
int main(int argc, char const *argv[])
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int n,number=0;
inputdata>>n;
while(n>0)
{
list<string>names;
for(int i = 0;i < n;i++)
{
string name;
inputdata>>name;
names.push_back(name);
}
symmetricOrder(names);
outputdata<<"SET "<<(++number)<<endl;
copy(names.begin(),names.end(),ostream_iterator<string>(outputdata,"\n"));
cout<<"SET "<<(number)<<endl;
copy(names.begin(), names.end(), ostream_iterator<string>(cout, "\n"));
inputdata>>n;
}
inputdata.close();
outputdata.close();
return 0;
}
Question 3-2 boundary
Problem description
A program needs to be written to draw the boundary of a closed path in the bitmap as shown in Figure 3-1. The closed path travels counterclockwise along the grid line, that is, it always travels between the grids (thick lines in the figure). Thus, following the path, the boundary on the pixel is located on the "right" side of the path. The size of the bitmap is 32 × 32, and set the coordinates of the lower left corner as (0,0). A closed path in a bitmap must not pass through the edge of the bitmap or cross itself.
input
The first line of the input file contains an integer representing the number of test cases. Each test case contains two rows of data. The first row of data in the case is two integers x and y representing the coordinates of the start and end points of the closed path. The second line is a string. Each character in the string represents a walk in a closed path, where "W" represents west, "E" represents East, "N" represents north, "S" represents South and "." Indicates termination.
output
For each test case, output a line of information indicating the case number ("Bitmap #1" "Bitmap #2", etc.). Next, data representing 32 rows of pixels in the bitmap is output. Each line is represented as a 32 character string, and each character represents a pixel in the line. "X" indicates pixels on the path boundary, "." Represents pixels on non path boundaries
sample input
1
2 1
EENNWNENWWWSSSES.
sample output
Bitmap #1
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
.XXX...
X...X...
X...X...
X...X...
.X...X...
...XX...
Problem solving ideas
(1) Data input and output
According to the description of the input file format, the number of cases T should be read from the input file first. Then read the number of cases in turn: the first line contains X and Y representing the coordinates of the starting point, and the second line is a string representing the direction of each step of the closed path counterclockwise from the starting point (with "." As an end flag) path. For this path, the simulation travels counterclockwise from the starting point (x, y) and draws the boundary (pixels around the path). The bitmap data (two-dimensional array) with the peripheral boundary of the path is taken as the calculation result, and the result is written to the output file line by line according to the output format (one line of data in the two-dimensional array is also taken as one line).
Open input file inputdata Create output file outputdata from inputdata Read in T for t←1 to T do from inputdata Read in x, y from inputdata Read a line from to path bitmap←BORDER(path, x, y) take"Bitmap # i "write outpudata as a line for i←1 to 32 do take bitmap[i]Write as one line outputdata close inputdata close outpudata
Among them, the seventh line calls to simulate the process of moving counterclockwise along the path from (x, y), and then drawing the peripheral boundary of the path. BORDER(path, x, y) is the key to solve a case.
(2) The algorithmic process of handling a case
Will 32 × The bitmap of 32 is represented as a matrix bitmap[1... 32, 1... 32], which is initialized to each pixel bitmap[i, j] = "". The closed route path starts from the coordinates (x, y) and travels counterclockwise along the grid line. The boundary we want to identify is always on the periphery of the route, that is, if we travel on the route, the boundary is always on the right side of the traveler (see Figure 3-2). In this way, when moving in four different directions, the identification boundary should follow the following rules:
1 to the East: mark "X" at the pixel (x, y), and then increase x by 1.
2 to the West: X decreases by 1, and then mark "X" at the pixel (x, y+1).
3: increase y by 1, and then mark "X" at the pixel (x, y).
4. South: mark "X" at the pixel (x − 1, y), and then y decreases by 1.
According to this law, we have the pseudo code description of the algorithm shown below.
BORDER(path, x, y) Create bitmap array bitmap[1..32]And initialize each element as a string".............................." i←1 while path[i]≠ "." do if path[i]= "E" then bitmap[y][x] ←"X" x←x+1 else if path[i]= "W" then x←x-1 bitmap[y+1][x] ←"X" else if path[i]= "N" then y←y+1 bitmap[y][x] ←"X" else bitmap[y][x-1] ←"X" y←y-1 i←i+1 return bitmap
Algorithm 3-2 process of solving a case of "boundary" problem
The running time of the algorithm depends on the number of repetitions of the while loop in lines 3 to 15. Since each repetition simulates further along the path line (the second line i is initialized to 1, and the 15th line i increases by 1), the number of repetitions of the cycle is exactly the number of steps along the path, that is, the length n of the path. The operation in the loop body is to simulate the further of the line, which is nothing more than filling in "X" at the appropriate position of the bitmap according to the law of traveling around the path. The time must be Θ (1). Thus, the running time of algorithm 3-2 is Θ (n) Where n is the length of the path. The C + + implementation code of the algorithm to solve this problem is stored in the folder laboratory/Border, and readers can open the file border CPP study and trial run. For C + + code parsing, please read chapter 9.1 Description of procedure 9-2 in Section 2. In reality simulation, it is often necessary to skillfully organize the data reflecting the attributes of things according to the characteristics of things themselves, which can effectively improve the time-space efficiency of the problem-solving algorithm. Commonly used data organization methods include stack - reflecting the law of data first in and last out, queue - reflecting the law of data first in and first out, and priority queue - reflecting the law of arranging the order of data use according to the priority of data attributes, etc. Even, the description of attribute data of some things can be organized into interesting data structures. For example, a mathematical expression can be represented as a binary tree - the parent node represents the operator and the child node represents the operand
#include <fstream>
#include <iostream>
#include <vector>
#include <string>
#include <iterator>
using namespace std;
vector<string> border(string path,int x,int y)
{
vector<string> bitmap(32,"................................");
int i = 0;
while(path[i] != '.')
{
switch(path[i])
{
case 'E':
bitmap[32-y][x++] = 'X';
break;
case 'W':
bitmap[31-y][--x]='X';
break;
case 'N':
bitmap[32 - (++y)][x] = 'X';
break;
case 'S':
bitmap[32 - (y--)][x - 1] = 'X';
break;
default:
break;
}
i++;
}
return bitmap;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int T;
inputdata >> T;
for(int t=0;t<T;t++)
{
int x,y;
inputdata>>x>>y;
string path;
getline(inputdata,path);
getline(inputdata,path);
vector<string> bitmap = border(path,x,y);
copy(bitmap.begin(), bitmap.end(), ostream_iterator<string>(outputdata, "\n"));
copy(bitmap.begin(), bitmap.end(), ostream_iterator<string>(cout, "\n"));
}
inputdata.close();
outputdata.close();
return 0;
}
Stack and its application
The so-called "stack" is a variation of the linear table: the addition and deletion of data elements are limited to the same end of the linear table. The first element added is called "stack bottom", and the last element added is called "stack TOP", which is recorded as TOP. The operation of adding elements to the stack is called "stacking" and is recorded as PUSH. The operation of deleting the TOP element of the stack is called "out of the stack"
, recorded as POP. As shown in Figure 3-3.
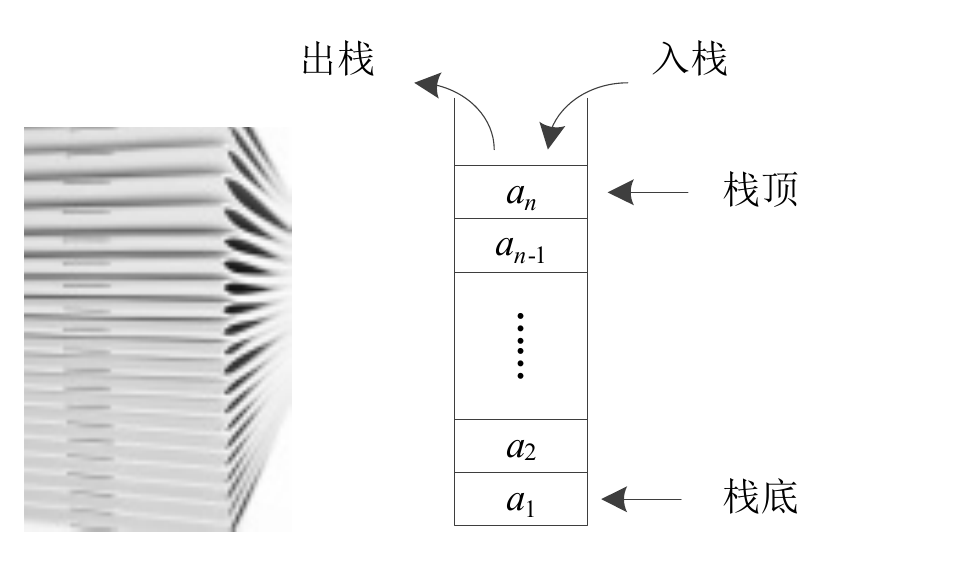
If an array is used to store the elements added to the stack S and maintain the attribute top (initially 0) representing the subscript of the element at the top of the stack, algorithm 3-3 describes several common stack operations
TOP(S) if S ≠∅ then return S[top[S]] else return NIL
PUSH(S, e) top[S]← top[S]+1 S[top[S]]←e POP(S) if S ≠∅ then top[S]← top[S]-1
Since insert and delete operations are limited to the end of the array, the running time of all these operations is constant Θ (1).
Question 3-3 Web navigation
Problem description
Standard Web browsers include the ability to turn pages back and forth. One way to achieve this is to use two stacks to track the Web page trace, so that the specified page can be reached through backward or forward operation. In this question, you are required to achieve this goal. The following commands need to be supported:
BACK: push the current page into the FORWARD stack. Pop up the BACK stack top page and set it as the new current page. If the backward stack is empty, this command is ignored. FORWARD: push the current web page into the backward stack. Pop up the top page of the FORWARD stack and set it as the new current page. If the FORWARD stack is empty, this instruction is ignored. VISIT: press the current web page into the BACK stack and set the URL as the new current web page. Clear FORWARD page. QUIT: exit the browser.
Assume that the browser's initial load URL is http://www.acm.org/ Web page
input
Input is a series of instructions. The instruction keywords are BACK, FORWARD, VISIT and QUIT, all in uppercase. Each URL has no white space characters and no more than 70 characters.
output
For each command except the QUIT command, if the command is not Ignored, the URL of the current page is output after executing the command. Otherwise, output "Ignored". The output of each instruction should occupy one line. No information is output for QUIT instruction.
sample input
VISIT http://acm.ashland.edu/
VISIT http://acm.baylor.edu/acmicpc/
BACK
BACK
BACK
FORWARD
VISIT http://www.ibm.com/
BACK
BACK
FORWARD
FORWARD
FORWARD
QUIT
sample output
http://acm.ashland.edu/
http://acm.baylor.edu/acmicpc/
http://acm.ashland.edu/
http://www.acm.org/
Ignored
http://acm.ashland.edu/
http://www.ibm.com/
http://acm.ashland.edu/
http://www.acm.org/
http://acm.ashland.edu/
http://www.ibm.com/
Ignored
Problem solving ideas
(1) Data input and output
According to the format of the input file, we should read each instruction line by line from the input file until we read QUIT. Store each instruction (except QUIT) in the array cmds in turn. Call the browser simulation process to execute various instructions, and store the execution results in the array result one by one. Finally, each element in the result is written to the output file as a line.
Open input file inputdata Create output file outputdata Create array cmds←∅ from inputdata Read a line from to cmd while cmd≠"QUIT" do INSERT(cmds, cmd) from inputdata Read in cmd result←WEB-NAVIGATION(cmds) for each r∈result do take r Write as one line outpudata close inputdata close outpudata
Among them, line 8 calls the process of simulating web browser, and WEB-NAVIGATION(cmds) is the key to solve a case.
(2) The algorithmic process of handling a case
According to the question prompt, it is necessary to maintain two stacks FORWARD stack and BACK stack (initialized as empty set ∅) and a current URL representing the currently accessed page address (initialized as“ http://www.acm.org/ ”)To simulate the process of turning pages BACK and forth when surfing the Internet. In addition to QUIT, the browser responds to three operations, namely BACK, FORWARD and VISIT.
BACK ( ) if back-stack≠∅ then PUSH(forward-stack, current-url) current-url←TOP(back-stack) POP(back-stack) return true return false FORWARD( ) if forward-stack≠∅ then PUSH(back-stack, current-url) current-url←TOP(forward-stack) POP(forward-stack) return true return false VISIT(url) PUSH(back-stack, current-url) current-url←url while forward-stack≠∅ do POP(forward-stack)
Using the above operations, the process of simulating a browser for Web navigation can be described as follows.
WEB-NAVIGATION(cmds) n←length[cmds], result←∅ forward-stack←∅, back-stack←∅ current-url←"http://www.acm.org/" for i ←1 to n do from cmds[i]The directive character is parsed from the cmd aline←"Ignored" if cmd="BACK" and BACK()=true then aline←current-url else if command="FORWARD" and FORWARD()=true then aline←current-url else if command="VISIT" then from cmds[i]Parse out parameters url VISIT(url) aline←current-url INSERT(result, aline) return result
Algorithm 3-4 algorithm process for solving "Web navigation" problem
Set the number of instructions in the input file to n. Because of the three functional processes BACK, FORWARD and VISIT, only the last repeated stack clearing operation (the while loop in lines 3 ~ 4 in the VISIT process) takes time Θ (n) , the other two take Θ (1). In the process of WEB-NAVIGATION, the for loop in lines 2 ~ 15 repeats n, so its running time is at most N 2, i.e Θ (n 2)
#include <fstream>
#include <iostream>
#include <sstream>
#include <stack>
#include <vector>
#include <string>
#include <iterator>
using namespace std;
class Brower
{
stack<string> fowardStack,backStack;
string currentUrl;
public:
Brower(string Url):currentUrl(Url){}
private:
bool back()
{
if(!backStack.empty())
{
fowardStack.push(currentUrl);
currentUrl=backStack.top();
backStack.pop();
return true;
}
return false;
}
bool foward()
{
if(!fowardStack.empty())
{
backStack.push(currentUrl);
currentUrl=fowardStack.top();
fowardStack.pop();
return true;
}
return false;
}
void visit(string url)
{
backStack.push(currentUrl);
currentUrl=url;
while(!fowardStack.empty())
{
fowardStack.pop();
}
}
public:
vector<string> webNavigation(vector<string> &commands)
{
int n = commands.size();
vector<string> result;
for(int i = 0;i<n;i++)
{
istringstream strstr(commands[i]);
string cmd,aline="Ignored";
strstr>>cmd;
if(cmd=="BACK" && back())
{
aline=currentUrl;
}
else if(cmd=="FORWARD" && foward())
{
aline=currentUrl;
}
else if(cmd=="VISIT")
{
string url;
strstr>>url;
visit(url);
aline=currentUrl;
}
result.push_back(aline);
}
return result;
}
};
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
string command;
vector<string>cmds;
getline(inputdata,command);
while(command!="QUIT")
{
cmds.push_back(command);
getline(inputdata,command);
}
Brower brower("http://www.acm.org/");
vector<string> result=brower.webNavigation(cmds);
copy(result.begin(), result.end(), ostream_iterator<string>(cout, "\n"));
copy(result.begin(), result.end(), ostream_iterator<string>(outputdata, "\n"));
inputdata.close();
outputdata.close();
return 0;
}
Question 3-4 periodic sequence
Problem description
Given function f:{0... N} → {0... N}. Where n is a nonnegative integer. For a given nonnegative integer n ≤ n, an infinite sequence can be constructed F = f 1 ( n ) , f 2 ( n ) , . . . , f k ( n ) , . . . F={ f^1 (n), f^2 (n), ..., f^k(n), ...} F=f1(n),f2(n),...,fk(n),.... Among them, f k ( n ) f^k(n) fk(n) is defined as f 1 ( n ) = f ( n ) f^1(n) = f(n) f1(n)=f(n) and f k + 1 ( n ) = f ( f k ( n ) ) f^{k+1}(n) = f(f^k(n)) fk+1(n)=f(fk(n)).
It is not difficult to see that each such sequence eventually has a period. That is, starting from a certain item, the subsequent data items are repeated, such as {1, 2, 7, 5, 4, 6, 5, 4, 6, 5, 4, 6,...}. For a given nonnegative integer n ≤ 11000000, n ≤ N and functional relationship F, it is required to calculate the period of sequence F.
Each line of input contains the integers n and N and the expression of the function F. Where f is given as a suffix, and the suffix expression is also called Reverse Polish Notation (abbreviated as (RPN)). The operands in the expression are unsigned integer constants, symbols representing integer n, and variable symbols x. Operators are all binary operations, including: + (add), * (multiply) and% (modulus, that is, the remainder of integer division). Operands and operators are separated by a space. The operator% occurs only once in the expression and is at the end of the expression. Its second operand must be the symbol representing n. The following functions:
2 x * 7 + N %
It is an RPN, which is converted into an equivalent suffix expression of (2*x+7)%N. The value of N in the last line of input is 0, which indicates the end of input. No processing is required for this line of data. For each row in the input, the output row contains only an integer representing the period of the sequence F corresponding to the given input data row.
sample input
10 1 x N %
11 1 x x 1 + * N %
1728 1 x x 1 + * x 2 + * N %
1728 1 x x 1 + x 2 + * * N %
100003 1 x x 123 + * x 12345 + * N %
0 0 0 N %
sample output
1
3
6
6
369
Problem solving ideas
(1) Data input and output
Process each test case in sequence according to the input file format. Each line in the file represents a test case. Where, the beginning is two integers N,n representing the value of modulus and variable x. Then there is a string of symbols for inverse Polish. The inverse Polish expression is expressed as a character array RPN, the sequence period value composed of this expression is calculated for the case data N,n and RPN, and the calculated result is written into the output file as a line. n=0 and n=0 is the input end flag.
Open input file inputdata Create output file outputdata from inputdata Read a row from s from s Resolved in N and n while N>0 or n>0 do take s Make the remaining symbols in the string RPN result←EVENTUALLY-PERIODIC-SEQUENCE(N, n, RPN) take result Write as one line outputdata from inputdata Read a line from to s from s Resolved in N and n close inputdata close outpudata
Among them, line 7 calls the process EVENTUALLY-PERIODIC-SEQUENCE(N, n, RPN) to calculate the minimum cycle of the cycle sequence, which is the key to solving a case.
(2) The algorithmic process of handling a case
There are two key points to solve this problem: first, how to calculate the function value according to the inverse Polish formula expressed as a string; Secondly, how to find the sequence f ( x ) , f 2 ( x ) , . . . , f k ( x ) , . . . f(x), f^2(x), ..., f^k(x), ... f(x),f2(x),...,fk(x),... Minimum period in. For the former, we can use a stack S to calculate the value of the expression when analyzing the inverse Polish formula. For example, for the string "x x 1 + * N%" in the input sample, figure 3-4 shows the calculation process.
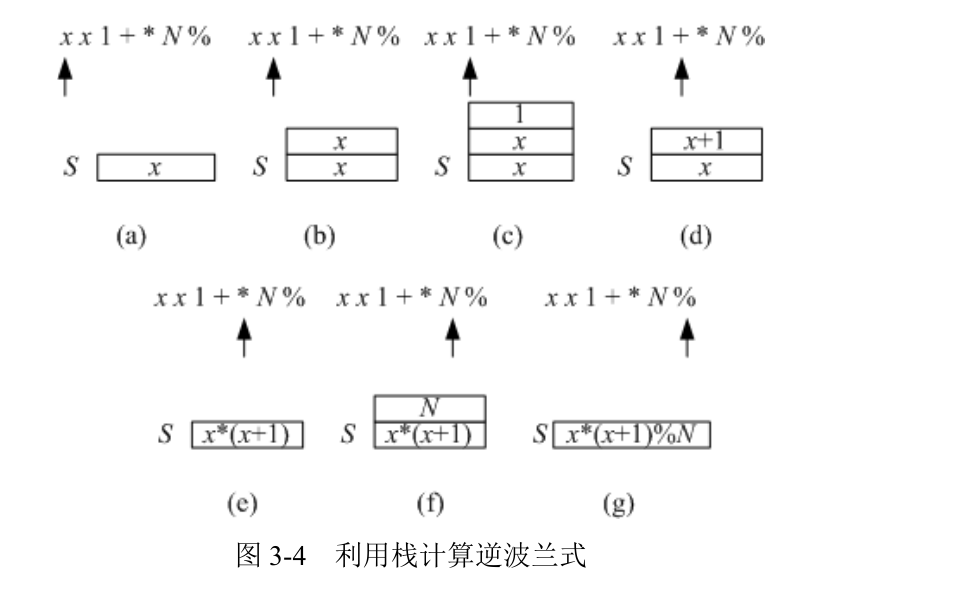
In Fig. 3-4, (a) analyze the first operand X in the formula and press it into the stack S; (b) Analyze the second operand X and press it into stack s; © Analyze to the third operand 1 and press into stack S; (d) Analyze the operator "+", pop up the two operands 1 and X in s, add them and press them into stack S; (e) Analyze the operator "" and pop up the two operands x+1 and X in s, multiply and press into S; (f) Analyze the operand N and press the stack; (g) Analyze the operator '%', pop up the two operands N and x(x+1) in s, and press the obtained result x*(x+1)%N on the stack after calculation.
We express the process of calculating f(x) from the inverse Polish RPN, independent variable value x and module N as the following pseudo code.
CALCULATE(N, x, RPN)
S←∅ Set empty stack
n←length[RPN]
for i←1 to n
do if RPN[i]∈{'+', '*', '%'} If operator
then op2←POP(S) From stack S Pop up the second operand
op1←POP(S) From stack S Pop up the first operand in the
if RPN[i]='+' If the operator is"+"
then PUSH(S, op1+op2) Calculate the sum of the two numbers and push them into the stack
else if RPN[i]='*' If the operator is"*"
then PUSH(S, op1*op2) Stack the backlog of two numbers
else PUSH(S, op1%op2) Operator is"%"
else if RPN[i]= 'x'
then PUSH(S, x) Is an operand x
else if RPN[i]= 'N'
then PUSH(S, N) Is an operand N
else d←RPN[i] Is a general operand, Convert to integer
PUSH(S, d)
return POP(S)
Algorithm 3-5 algorithm process of calculating inverse Polish expression
The running time of the algorithm depends on the number of for loop repetitions n in lines 3 ~ 17. It takes time to repeat any branch in the if branch structure each time Θ (1) (this is because the time-consuming operations of pressing stack and bouncing stack of stack S are Θ (1)). Therefore, the running time of algorithm 3-5 is Θ (n). For the latter, we initialize x to N and set A set A (initialized to ∅) to store fk(x)(k=0, 1,...). As long as X ∉ A, save X and its serial number k in A. Then, using the CALCULATE process, CALCULATE fk+1(x) and give x,k self increment 1 as the starting point of the next round of calculation. Cycle until x ∈ A. The difference k-i between the sequence number k of the current X and the sequence number I of the found equal element is the minimum cycle of the x value, which is returned.
EVENTUALLY-PERIODIC-SEQUENCE(N, n, RPN) k←0 Create collection A←∅ x←n while x∉A do INSERT(A, (x, k)) k←k+1 x← CALCULATE(N, x, RPN) i ← x stay A Serial number in return k-i
Algorithm 3-6 algorithm process for solving "periodic sequence" problem
Let the while loop on lines 4 to 8 of the algorithm repeat m times. Since there are only two dictionary operations for set A: insert (line 5) and find (condition detection in line 4), both operations are time-consuming if A is represented as A hash table Θ (1) (see table 2-1). According to the above analysis of the algorithm process CALCULATE, the time consumption in line 7 is Θ (n). Therefore, the running time of the algorithm is Θ (nm).
#include <fstream>
#include <iostream>
#include <sstream>
#include <vector>
#include <map>
#include <stack>
#include <string>
using namespace std;
int calculate(int N, int x, vector<string> RPN)
{
stack<unsigned long long> S;
int n = RPN.size();
string operators = "+*%";
for (int i = 0; i < n; i++)
{
size_t op = operators.find(RPN[i]);
if (op <= 2)
{
unsigned long long op2 = S.top(); S.pop();
unsigned long long op1 = S.top(); S.pop();
switch (op)
{
case 0: //"+"
S.push(op1 + op2);
break;
case 1: //"*"
S.push(op1 * op2);
break;
case 2://"%"
S.push(op1 % op2);
break;
default:
break;
}
}
else
{
if (RPN[i] == "x")
S.push(x);
else if (RPN[i] == "N")
S.push(N);
else S.push(int(atoi(RPN[i].c_str())));
}
}
return S.top();
}
int eventuallyPeriodicSequence(int N, int n, vector<string> &RPN)
{
int k = 0, x = n;
map<int, int>A;
int i = A[x];
while (!i)
{
A[x] = ++k;
x = calculate(N, x, RPN);
i = A[x];
}
return k - i + 1;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int N, n;
inputdata >> N >> n;
while (N > 0 || n > 0)
{
string s, item;
getline(inputdata, s);
istringstream strstr(s);
vector<string>RPN;
while (strstr >> item)
{
RPN.push_back(item);
}
int result = eventuallyPeriodicSequence(N, n, RPN);
outputdata << result << endl;
cout << result << endl;
inputdata >> N >> n;
}
inputdata.close();
outputdata.close();
return 0;
}
Queue and its application
The so-called queue is also a variation of the linear table: the insertion and deletion of elements are limited to the tail and head of the linear table respectively. In this way, the data elements in the queue meet the characteristics of first in first out, just like people queuing for services, as shown in Figure 3-5. The operation of adding elements to the queue to become the end of the queue is called "joining the queue", and the operation of deleting the head of the queue is called "leaving the queue".
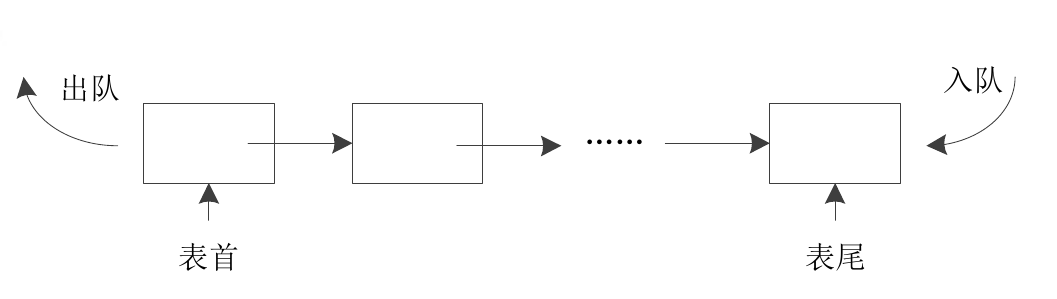
Similar to the stack operation, queue in operation and queue out operation are represented as PUSH and POP respectively. Queues are usually implemented with linked lists. In addition, three attributes need to be maintained: the number of elements in the queue n, the head of the queue and the tail of the queue.
PUSH(Q, e) crate node x with value e next[tail]←x next[tail]←NIL tail←x
POP(Q) if Q≠∅ then head← next[head] FRONT(Q) return head
Since it only takes a constant time to add and delete elements at both ends of the linked list, the running time of the queue in PUSH and out POP operations in algorithm 3-7, including reading the first element of the queue, is the same Θ (1).
Question 3-5 stable marriage
Problem description
The problem of stable marriage refers to the problem of seeking the corresponding relationship between the members of one set and the members of another set according to the degree of admiration. Input to the question includes:
A set of n males M. A set F of n women. Every man and every woman has a table of their admiration for the opposite sex. The list in the table is sorted according to the degree of admiration, from favorite to least favorite. Marriage is a 1-1 correspondence between male set and female set. Marriage a is said to be stable. If there is no ordered couple < F, M > so that f ∈ f likes m ∈ m more than his partner, and M likes f more than his partner. Stable marriage a is called male priority. If there is no stable marriage B, any male in B likes his partner more than his partner in a. Given each male and female's degree of admiration for the opposite sex, find out that men give priority to stable marriage.
input
The first line of input gives the number of test cases T. The first line of each test case contains an integer n (0 < n < 27). The next line describes the names of N men and N women (the first n letters). Male names are in lowercase letters and female names are in uppercase letters. The next N lines describe how much each man loves each woman. The last n lines describe how much each woman admires each man.
output
For each test case, the stable marriage with male priority is output. The sequence pairs in the test case are arranged in the order of the male name dictionary, as shown in the output example. Test cases are separated by blank lines.
sample input
2
3
a b c A B C
a:BAC
b:BAC
c:ACB
A:acb
B:bac
C:cab
3
a b c A B C
a:ABC
b:ABC
c:BCA
A:bac
B:acb
C:abc
sample output
a A
b B
c C
a A
b B
c C
According to the format description of the input file, first read the number of cases T. Then read the input data of each case in turn. The first row of data in each case is an integer n indicating how many boys and girls each have, and the row indicating the identification of boys and girls is omitted. Read the likes of N boys to girls in turn and store them in dictionary F. Read the likes of n girls to boys in turn and store them in the dictionary M. For F and m, calculate the n most stable marriages formed by the cooperation of N boys and n girls. Write the calculation results to the output file in the order of boys' identifier dictionary, one couple per line, and output a blank line before the end.
Open input file inputdata Create output file outputdata from inputdata Number of cases read from T for t←1 to T do from inputdata Read the number of boys and girls in n Skip inputdata Middle school boys and girls are OK Create dictionary F←∅ for i←1 to n do from inputdata Read boy representation in f,And how much you like girls preference INSERT(F, (f, preference)) Create dictionary M←∅ for i←1 to n do from inputdata Read boy representation in m,And how much you like boys preference INSERT(M, (m, preference)) A←STABLE-MARRIAGE(M, F) SORT(A) for each couple∈A do take couple Write as one line outputdata towards outputdat Write a blank line close inputdata close outpudata
Among them, line 15 calls the process of calculating stable marriage (m, f), which is the key to solving a case.
(2) The algorithmic process of handling a case
For A case data f and m, A queue q is used to simulate the engagement process between men and women. Set A boy's proposal queue Q and engagement set A (initialized to an empty set). At the beginning, all men enter the marriage proposal queue Q, and then ask the first man m to propose to his favorite woman f who has not proposed. If the woman is not engaged, m,f are engaged, < F, M > enter marriage set A, and M is out of the queue. Otherwise, f has A fiance M ', that is < F, M' > ∈ A. At this time, if f prefers m, then < F, M '> cancel the engagement, m,f are engaged, m leaves the team and M' joins the team. Otherwise, m propose to the next woman you like. Write this process as pseudo code as follows.
STABLE-MARRIAGE(M, F) A←∅ Marriage collection Q←M Proposal queue while Q≠∅ do m←FRONT(Q) m Head of the team f←F in m Never pursued and m The most adored if f single then INSERT(A, <f, m>) f, m be engaged POP(Q) m Out of the team else if <f, m'>∈A and f More admiration m then DELETE(A, <f, m'>) f, m'Dissolution of engagement INSERT(A, <f, m>) f, m be engaged POP(Q) m Out of the proposal queue PUSH(Q, m') m'Rejoin the proposal queue return A
Algorithm 3-8 algorithm process for solving a case of "stable marriage"
Let the number of boys and girls be n. The worst case is that every boy has to propose n times to get true love. In this way, the while loop on lines 3 to 12 will repeat Θ (n2) times. The time-consuming of queue in, queue out and accessing the head of queue Q in each cycle is constant Θ (1). If f and m are represented as hash tables, the time-consuming search operation of line 5 in F is Θ (1). If engagement set A is represented as A binary search tree (because it needs to be sorted before output in addition to dictionary operation on A), the insertion operation on line 7 and 11, the search operation on line 9 and the deletion operation on line 10 are time-consuming Θ (LGN) (see table 2-1). Therefore, the running time of algorithm 3-8 is Θ (n2lgn). The C + + implementation code of the algorithm to solve this problem is stored in the folder laboratory/The Stable Marrige. Readers can open the file the stable marrige CPP study and trial run. For C + + code parsing, please read chapter 9.5 Description of procedure 9-65 ~ procedure 9-67 in Section 3
#include <iostream>
#include <fstream>
#include <queue>
#include <string>
#include <set>
#include <map>
#include <iterator>
using namespace std;
struct Male
{
string pref;
size_t current;
Male(string p = ""): pref(p), current(0) {}
};
struct Female
{
string pref;
bool engaged;
Female(string p = ""): pref(p), engaged(false) {}
};
struct Couple
{
char female, male;
Couple(char f = ' ', char m = ' '): female(f), male(m) {}
};
bool operator==(const Couple &a, const Couple &b)
{
return a.female == b.female;
}
bool operator<(const Couple &a, const Couple &b)
{
return a.male < b.male;
}
ostream &operator<<(ostream &out, const Couple &a)
{
out << a.male << " " << a.female;
return out;
}
set<Couple, less<Couple>> stableMarriage(map<char, Male> &M,
map<char, Female> &F)
{
set<Couple, less<Couple>> A;
queue<char> Q;
map<char, Male>::iterator a;
for (a = M.begin(); a != M.end(); a++)
Q.push(a->first);
while (!Q.empty())
{
char m = Q.front();
char f = M[m].pref[M[m].current++];
if (!F[f].engaged)
{
A.insert(Couple(f, m));
F[f].engaged = true;
Q.pop();
}
else
{
set<Couple, less<Couple>>::iterator couple =
find(A.begin(), A.end(), Couple(f));
char m1 = couple->male;
if ((F[f].pref).find(m) < (F[f].pref).find(m1))
{
A.erase(Couple(f, m1));
A.insert(Couple(f, m));
Q.pop();
Q.push(m1);
}
}
}
return A;
}
int main()
{
ifstream inputdata("inputdata.txt");
ofstream outputdata("outputdata.txt");
int t;
inputdata>>t;
for(int i = 0;i<t;i++)
{
int n;
string aline;
inputdata>>n;
map<char,Male>M;
map<char,Female>F;
getline(inputdata,aline,'\n');
getline(inputdata,aline,'\n');
for(int j=0;i<n;j++)
{
getline(inputdata,aline,'\n');
char name=aline[0];
string preference=aline.substr(2,n);
M[name]=Male(preference);
}
for(int j=0;j<n;j++)
{
getline(inputdata,aline,'\n');
char name=aline[0];
string preference=aline.substr(2,n);
F[name]=Female(preference);
}
set<Couple,less<Couple>> A=stableMarriage(M,F);
copy(A.begin(),A.end(),ostream_iterator<Couple>(outputdata, "\n"));
outputdata<<endl;
copy(A.begin(),A.end(),ostream_iterator<Couple>(cout, "\n"));
cout<<endl;
}
inputdata.close();
outputdata.close();
return 0;
}