HashMap is a Map interface implementation based on hash table. It exists in the form of key value storage, that is, it is mainly used to store key value pairs. Among them, key value can be null, and the mapping is not orderly. The implementation of HashMap is not synchronous, that is, the thread is not safe.
1, Storage characteristics
1.1 evolution of data structure
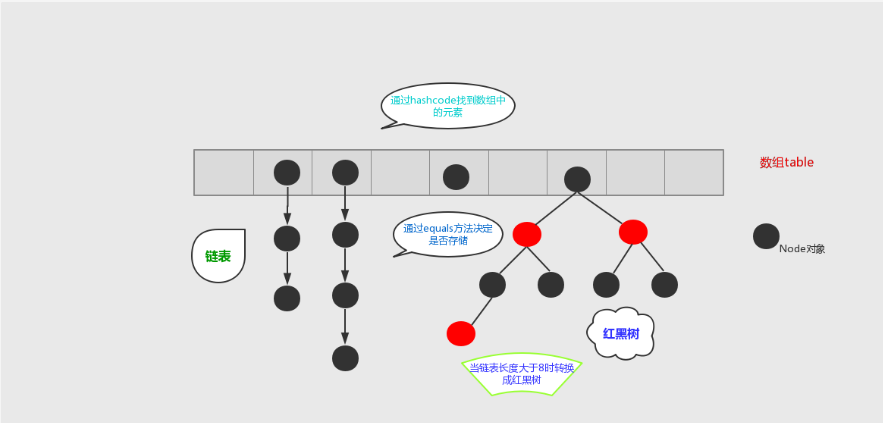
jdk1.7 -: it is composed of array + linked list. The array is the main body. The linked list mainly exists to solve hash conflicts (i.e. the array index values calculated through the key are the same) (the "zipper method" solves conflicts).
jdk1.8 +: it is composed of array + linked list + red black tree. There are great changes in resolving hash conflicts. When the length of the linked list is greater than the threshold (the boundary value of the red black tree is 8 by default) and the current array length is greater than 64, the data storage structure at this index position will be transformed into a red black tree.
Add: before the linked list is converted into a red black tree, even if the threshold is greater than 8, but the array length is less than 64, the linked list will not be changed into a red black tree, but the capacity of the array will be expanded.
The purpose is to avoid the red black tree structure when the array is small. Because when the array is small, it will become a red black tree structure, which will reduce the efficiency (the red black tree needs to perform left-hand rotation, right-hand rotation and color change to maintain balance). At the same time, when the array length is less than 64, the search time is relatively faster. Therefore, as mentioned above, in order to improve performance, the linked list is converted to a red black tree only when the underlying threshold is greater than 8 and the array length is greater than 64. For details, please refer to the treeifyBin() method.
Of course, although the red black tree is added as the underlying data structure, the structure becomes complex, but when the threshold is greater than 8 and the array length is greater than 64, the efficiency becomes more efficient when the linked list is converted to red black tree.
1.2 features
- Storage out of order.
- The key and value can be null, but only one null can exist at the key position.
- The key position is unique and controlled by the underlying data structure.
- jdk1. The data structure before 8 is linked list + array, jdk1 8 followed by linked list + array + red black tree.
- Only when the threshold value (boundary value) > 8 and the array length is greater than 64 can the linked list be converted into a red black tree. The purpose of changing into a red black tree is to provide super query.
2, Class structure
2.1 inheritance
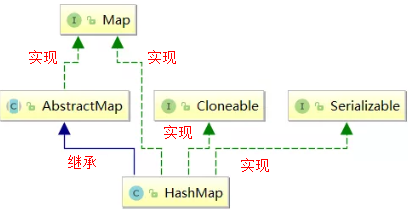
explain:
- Cloneable is an empty interface, indicating that it can be cloned. Create and return a copy of the HashMap object.
- Serializable serialization interface. Tag HashMap objects can be serialized and deserialized.
- AbstractMap provides a Map implementation interface. To minimize the effort required to implement this interface.
Question: through the above inheritance relationship, we find a very strange phenomenon, that is, HashMap has inherited AbstractMap, and AbstractMap class implements the Map interface. Why is HashMap implementing the Map interface? This structure is also found in ArrayList and LinkedLis.
Answer: according to Josh Bloch, founder of the Java collection framework, this writing is a mistake. In the Java collection framework, there are many ways to write like this. When he first wrote the Java collection framework, he thought it might be valuable in some places until he realized that he was wrong. Obviously, jdk maintainers didn't think this small mistake was worth modifying, so they kept it.
2.2 member variables
public class HashMap<K, V> extends AbstractMap<K, V>
implements Map<K, V>, Cloneable, Serializable {
/** Serialized version number */
private static final long serialVersionUID = 362498820763181265L;
/** The set initialization capacity must be the n-th power of 2. The default initial capacity is 16 */
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
/** The maximum capacity of the collection. The default is the 30th power of 2 */
static final int MAXIMUM_CAPACITY = 1 << 30;
/** Default load factor, default 0.75 */
static final float DEFAULT_LOAD_FACTOR = 0.75f;
/** When the number of elements in the linked list exceeds this value, it will turn into a red black tree (new in jdk1.8) */
static final int TREEIFY_THRESHOLD = 8;
/** When the value of the linked list is less than 6, it will be transferred back from the red black tree to the linked list */
static final int UNTREEIFY_THRESHOLD = 6;
/** When the number of stored elements exceeds this value, the bucket in the table can be converted into a red black tree. Otherwise, the bucket will only be expanded when the elements in the bucket exceed the specified conditions */
static final int MIN_TREEIFY_CAPACITY = 64;
/** Array structure */
transient Node<K,V>[] table;
/**Store cached data */
transient Set<Entry<K,V>> entrySet;
/**Number of stored elements */
transient int size;
/** It is used to record the modification times of HashMap, that is, the counter for each expansion and change of map structure */
transient int modCount;
/** Capacity expansion critical value: when the number of stored elements exceeds the critical value (capacity * load factor), capacity expansion will be carried out */
int threshold;
/** Hash table load factor */
final float loadFactor;
}
2.3 construction method
2.3.1 HashMap(initialCapacity, loadFactor)
/**
* Constructor specifying capacity size and load factor
* @param initialCapacity capacity
* @param loadFactor Load factor
*/
public HashMap(int initialCapacity, float loadFactor) {
// Judge whether the initialization capacity is less than 0
if (initialCapacity < 0)
// If it is less than 0, an illegal parameter exception, IllegalArgumentException, is thrown
throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity);
// Judge whether the initialization capacity initialCapacity is greater than the maximum capacity of the set_ CAPACITY
if (initialCapacity > MAXIMUM_CAPACITY)
// If maximum is exceeded_ Capability, the maximum_ Capability is assigned to initialCapacity
initialCapacity = MAXIMUM_CAPACITY;
// Judge whether the load factor loadFactor is less than or equal to 0 or whether it is a non numeric value
if (loadFactor <= 0 || Float.isNaN(loadFactor))
// If one of the above conditions is met, an illegal parameter exception IllegalArgumentException is thrown
throw new IllegalArgumentException("Illegal load factor: " + loadFactor);
// Assign the specified load factor to the load factor loadFactor of the HashMap member variable
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
/*
* Returns the n-th power of the smallest 2 larger than the specified initialization capacity
* @param capacity
*/
static final int tableSizeFor(int cap) {
// Prevent cap is already a power of 2. If cap is already a power of 2 and there is no minus 1 operation,
// After performing the following unsigned operations, the returned apacity will be twice that of this cap.
int n = cap - 1;
n |= n >>> 1; // The highest non-zero bit shifts to the right by 1 bit, logic or n, and the highest 2 bits can be 11
n |= n >>> 2; // The highest non-zero 2 bits are shifted to the right by 2 bits, logic or n. at this time, the highest 2 bits can be 1111
n |= n >>> 4; ...
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
Note: in the tablesizefor method, the calculated data is returned to the call, and directly assigned to the threshold boundary value. Some people will think this is a bug. It should be written like this threshold = tableSizeFor(initialCapacity) * this. LoadFactor, so as to meet the meaning of threshold (the capacity will be expanded when the size of HashMap reaches the threshold). However, please note that in the construction methods after jdk8, the member variable table is not initialized. The initialization of table is postponed to the put method, where the threshold will be recalculated.
2.3.2 HashMap(Map<?, ?> m)
// Construct a new HashMap with the same mapping relationship as the specified Map.
public HashMap(Map<? extends K, ? extends V> m) {
// The load factor loadFactor changes to the default load factor of 0.75
this.loadFactor = DEFAULT_LOAD_FACTOR;
putMapEntries(m, false);
}
final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {
//Gets the length of the parameter set
int s = m.size();
if (s > 0) { // Determine whether the parameter set contains elements
if (table == null) { // Determine whether the table has been initialized
// Uninitialized, s is the actual number of elements of m
float ft = ((float)s / loadFactor) + 1.0F;
int t = ((ft < (float)MAXIMUM_CAPACITY) ? (int)ft : MAXIMUM_CAPACITY);
// If the calculated t is greater than the threshold, reinitialize the threshold
if (t > threshold)
threshold = tableSizeFor(t);
}
// It has been initialized and the number of m elements is greater than the threshold value. Capacity expansion is required
else if (s > threshold)
resize();
// Add all elements in m to HashMap
for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) {
K key = e.getKey();
V value = e.getValue();
putVal(hash(key), key, value, false, evict);
}
}
}
Question: why add 1.0F in the line float ft = ((float)s / loadFactor) + 1.0F?
The result of s/loadFactor is decimal, plus 1.0F, (int)ft, which is equivalent to rounding up the decimal to ensure greater capacity as much as possible, which can reduce the number of calls to resize. So + 1.0F is to get more capacity.
2.4 membership method
2.4.1 adding node elements
The put method is complex, and the implementation steps are as follows:
- First, calculate the bucket to which the key is mapped through the hash value;
- If there is no collision on the barrel, insert it directly;
- If a collision occurs, you need to deal with the conflict:
a. If the bucket uses a red black tree to handle conflicts, the method of the red black tree is called to insert data;
b. Otherwise, the traditional chain method is used to insert. If the length of the chain reaches the critical value, the chain is transformed into a red black tree; - If there is a duplicate key in the bucket, replace the key with the new value value;
- If the size is greater than the threshold, expand the capacity;
The specific methods are as follows:
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
static final int hash(Object key) {
int h;
/*
1)If key equals null: the returned value is 0
2)If the key is not equal to null: first calculate the hashCode of the key, assign it to h, and then move it 16 bits to the right without sign with H
Binary performs bitwise XOR to get the final hash value
*/
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
Question: (H = key. hashCode()) ^ (H > > > 16), the high 16bit remains unchanged, the low 16bit and high 16bit do an XOR, and the obtained hashCode is converted to 32-bit binary. Why do you do this?
Answer: if n is the length of the array is very small, assuming 16, then n - 1 is 1111. This value and hashCode directly perform bitwise and operations. In fact, only the last four bits of the hash value are used. If the high-order change of the hash value is large and the low-order change is small, it is easy to cause hash conflict. Therefore, the high-order and low-order are used here to solve this problem.
2.4.2 adding node elements internally
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
/**
* @param hash key hash value of
* @param key Original key
* @param value Value to store
* @param onlyIfAbsent If true, the existing value will not be changed
* @param evict If false, it means that the table is in creation status
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// Judge whether the collection is newly created, that is, the tab is null
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// Calculate whether an element already exists at the node location. If it exists, it indicates that there is a collision conflict. Otherwise, insert the element directly into the location
// Save the existing bucket data to the variable p
if ((p = tab[i = (n - 1) & hash]) == null)
// Create a new node and store it in the bucket
tab[i] = newNode(hash, key, value, null);
else { // Execute else to explain that tab[i] is not equal to null, indicating that this location already has a value
Node<K,V> e; K k;
// 1. The element hash values are equal, but they cannot be determined to be the same value
// 2. Whether the key is the same instance or whether the values are equal
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
// Note: the hash values of the two elements are equal, and the value of the key is also equal. Assign the whole object of the old element to e and record it with E
e = p;
// hash values are not equal or key s are not equal; Judge whether p is a red black tree node
else if (p instanceof TreeNode)
// Put it in the tree
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else { // Description is a linked list node
// 1) If it is a linked list, you need to traverse to the last node and insert it
// 2) Loop traversal is used to judge whether there are duplicate key s in the linked list
for (int binCount = 0; ; ++binCount) {
// Determine whether p.next reaches the tail of the linked list
// Take out p.next and assign it to e
if ((e = p.next) == null) {
// Insert the node at the end of the linked list
p.next = newNode(hash, key, value, null);
// Judge whether the critical condition for converting to red black tree is met. If so, call treeifyBin to convert to red black tree
// Note: the treeifyBin method will check the array length if it is less than min_ TREEIFY_ Capability will expand the capacity of the array
if (binCount >= TREEIFY_THRESHOLD - 1)
// Convert to red black tree
treeifyBin(tab, hash);
// Jump out of loop
break;
}
// If the end of the linked list is not reached, judge whether the key value is the same
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
// Jump out of loop because e has been saved
break;
// It indicates that the newly added element is not equal to the current node. Continue to find the next node.
// Used to traverse the linked list in the bucket. Combined with the previous e = p.next, you can traverse the linked list
p = e;
}
}
// Indicates that a node whose key value and hash value are equal to the inserted element is found in the bucket
// In other words, duplicate keys are found through the above operation, so here is to change the value of the key into a new value and return the old value
// This completes the modification function of the put method
if (e != null) {
// Record the value of e
V oldValue = e.value;
// onlyIfAbsent is false or the old value is null
if (!onlyIfAbsent || oldValue == null)
// Replace old value with new value
// e.value represents the old value and value represents the new value
e.value = value;
// Post access callback
afterNodeAccess(e);
// Return old value
return oldValue;
}
}
// Number of records modified
++modCount;
// Judge whether the actual size is greater than the threshold. If it exceeds the threshold, expand the capacity
if (++size > threshold)
resize();
// Post insert callback
afterNodeInsertion(evict);
return null;
}
2.4.3 convert linked list to red black tree
After adding nodes, judge whether the number of nodes is greater than tree_ The threshold value of threshold is 8. If it is greater than, the linked list will be converted into a red black tree. The method is treeifyBin.
/**
* @param tab array
* @param hash Hash value
*/
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
// If the current array is empty or the length of the array is less than the threshold for tree formation (min_tree_capability = 64), the capacity will be expanded.
// Instead of turning the node into a red black tree.
// Objective: if the array is very small, it is less efficient to convert the red black tree and traverse it.
// At this time, if the capacity is expanded, the hash value will be recalculated, the length of the linked list may be shortened, and the data will be put into the array, which is relatively more efficient.
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
//Capacity expansion method
resize();
// Get the bucket element of the key hash value and judge whether it is empty
else if ((e = tab[index = (n - 1) & hash]) != null) {
// Perform steps
// 1. First convert the element into a red black tree node
// 2. Then set it as a linked list structure
// 3. Finally, the linked list structure is transformed into a red black tree
// hd: head node of red black tree tl: tail node of red black tree
TreeNode<K,V> hd = null, tl = null;
do {
// Replace the current bucket node with a red black tree node
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null) // For the first operation, the red black tree tail node is empty
hd = p; // Assign the p node of the new key to the head node of the red black tree
else {
p.prev = tl; // Assign the previous node p to the previous node of the current P
tl.next = p; // Take the current node p as the next node of the tail node of the tree
}
tl = p;
// Until the loop reaches the end of the linked list, and the linked list elements are replaced with red black tree nodes
} while ((e = e.next) != null);
// Let the first element in the bucket, that is, the element in the array, point to the node of the new red black tree,
// In the future, the elements in this bucket are red and black trees, not linked list data structures
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}
2.4.4 capacity expansion
When to expand: when the number of elements in the HashMap exceeds the array size (array length) * loadFactor, the array will be expanded. The default value of loadFactor is 0.75.
Capacity expansion will be accompanied by a re hash allocation, and all elements in the hash table will be traversed, which is very time-consuming. When writing programs, try to avoid resize.
The rehash method used by HashMap during capacity expansion is very ingenious, because each capacity expansion is doubled. Compared with the original calculated (n - 1) & hash result, there is only one bit more, so the node is either in the original position or assigned to the position of "original position + old capacity".
Therefore, during HashMap capacity expansion, you do not need to recalculate the hash. You only need to see whether the new bit of the original hash value is 1 or 0. If it is 0, the index remains unchanged, and if it is 1, the index becomes "original location + old capacity".
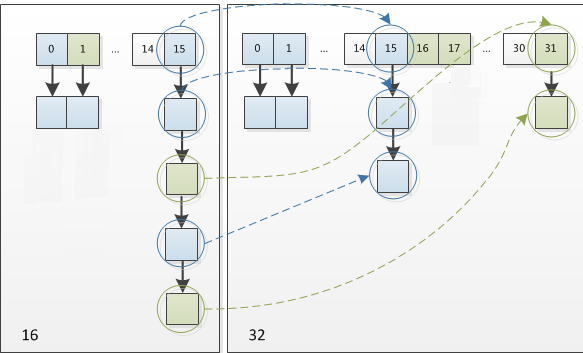
It is precisely because of this ingenious rehash method that not only saves the time to recalculate the hash value, but also because the newly added 1 bit is 0 or 1, it can be considered as random. In the process of resizing, it is ensured that the number of nodes on each bucket after rehash must be less than or equal to the number of nodes on the original bucket, so as to ensure that there will be no more serious hash conflict after rehash, The previously conflicting nodes are evenly dispersed into new buckets.
Interpretation of source code resize method
final Node<K,V>[] resize() {
// Get the current array
Node<K,V>[] oldTab = table;
// Returns 0 if the current array is equal to null length, otherwise returns the length of the current array
int oldCap = (oldTab == null) ? 0 : oldTab.length;
// The current threshold value is 12 (16 * 0.75) by default
int oldThr = threshold;
int newCap, newThr = 0;
// If the length of the old array is greater than 0, start to calculate the size after capacity expansion
// Less than or equal to 0, there is no need to expand the capacity
if (oldCap > 0) {
// If you exceed the maximum value, you won't expand any more, so you have to collide with you
if (oldCap >= MAXIMUM_CAPACITY) {
// Modify the threshold to the maximum value of int
threshold = Integer.MAX_VALUE;
return oldTab;
}
// Capacity expanded by 2 times
// The new capacity cannot exceed the size of 2 ^ 30
// The original capacity is greater than or equal to initialization DEFAULT_INITIAL_CAPACITY=16
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
// Double the threshold
newThr = oldThr << 1; // double threshold
}
// If the original capacity is less than or equal to 0 and the original threshold point is greater than 0
else if (oldThr > 0) // The original threshold is assigned to the new array length
newCap = oldThr;
else { // If it is not satisfied, the default value is used directly
newCap = DEFAULT_INITIAL_CAPACITY;//16
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
// If the original capacity is less than or equal to 0 and the original threshold point is greater than 0, then newThr is 0
// Calculate the new resize maximum upper limit
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
// The default value of the new threshold is 12 times 2 and then becomes 24
threshold = newThr;
// Create a new hash table
@SuppressWarnings({"rawtypes","unchecked"})
//newCap is the new array length
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
// Judge whether the original array is equal to null
if (oldTab != null) {
// Move each bucket into a new bucket
// Traverse each bucket of the original hash table and recalculate the new position of the elements in the bucket
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
// The original data is assigned null to facilitate GC recycling
oldTab[j] = null;
// Determines whether the array has a next reference
if (e.next == null)
// There is no next reference, indicating that it is not a linked list. There is only one key value pair on the current bucket, which can be inserted directly
newTab[e.hash & (newCap - 1)] = e;
// Judge whether it is a red black tree
else if (e instanceof TreeNode)
// If the description is a red black tree to handle conflicts, call relevant methods to separate the trees
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // Using linked list to deal with conflicts
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
// Calculate the new position of the node through the principle explained above
do {
// Original index
next = e.next;
// Here we judge that if it is equal to true e, the node does not need to move after resize
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
// Original index + oldCap
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
// Put the original index into the bucket
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
// Put the original index + oldCap into the bucket
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
2.4.5 deletion
The deletion method is to first find the location of the element. If it is a linked list, traverse the linked list to find the element and then delete it. If it is a red black tree, traverse the tree, and then delete it after finding it. When the tree is less than 6, turn the linked list.
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
/**
* @param hash Deletes the hash value of the element
* @param key Delete key of element
* @param value Delete the value of the element
* @param matchValue Does the value match
* @param movable Do you want to move the startup node after removing the element
*/
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
// Find the location according to the hash
// If the bucket mapped to the current key is not empty
// Assign the element corresponding to the bucket to traversal p
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
Node<K,V> node = null, e; K k; V v;
if (p.hash == hash && // If the node on the bucket is the key to be found, point the node to the node
((k = p.key) == key || (key != null && key.equals(k))))
node = p;
else if ((e = p.next) != null) { // Indicates that the node has a next node
if (p instanceof TreeNode)
// Note: if the conflict is handled by the red black tree, obtain the node to be deleted by the red black tree
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
else {
// Judge whether to handle hash conflicts in the way of linked list. If yes, traverse the linked list to find the node to be deleted
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
// Compare whether the value of the found key matches the key to be deleted
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
// Delete the node by calling the method of red black tree
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
else if (node == p)
// Linked list deletion
tab[index] = node.next;
else
p.next = node.next;
// Record modification times
++modCount;
// Number of changes
--size;
afterNodeRemoval(node);
return node;
}
}
return null;
}
2.4.6 finding elements
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
// If the hash table is not empty and the bucket corresponding to the key is not empty
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// Determine whether the array elements are equal
// Check the first element according to the position of the index
// Note: always check the first element
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
// If it is not the first element, judge whether there are subsequent nodes
if ((e = first.next) != null) {
// Judge whether it is a red black tree. If yes, call the getTreeNode method in the red black tree to obtain the node
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
// If it is not a red black tree, it is a linked list structure. Judge whether the key exists in the linked list through the circular method
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
3, Thinking questions
3.1 jdk8 why should red black trees be introduced?
Answer: jdk1 Before 8, the implementation of HashMap was array + linked list. Even if the hash function is better, it is difficult to achieve 100% uniform distribution of elements. When a large number of elements are stored in the same bucket, the bucket becomes a long linked list, so HashMap is equivalent to a single linked list. If the single linked list has n elements, the traversal time complexity is O(n), completely losing its advantages.
In this case, jdk1 8 introduces red black tree (the search time complexity is O(logn)) to optimize this problem. When the length of the linked list is very small, the traversal speed is very fast, but when the length of the linked list continues to grow, it will certainly have a certain impact on the query performance, so it needs to be transformed into a tree.
3.2 how to implement hash function in HashMap? What are the implementation methods of hash functions?
A: for the hashCode of the key, perform the hash operation, move the unsigned right 16 bits, and then perform the XOR operation.
There are also square middle method, pseudo-random number method and remainder method. These three kinds of efficiency are relatively low. The operation efficiency of unsigned right shift 16 bit XOR is the highest.
3.3 what happens when the hashcodes of two objects are equal?
A: hash collision will occur. If the content of the key value is the same, replace the old value. Otherwise, insert it at the end of the linked list. When the array length is greater than 64, if the length of the linked list exceeds the threshold 8, it will be converted to red black tree storage.
3.4 what is hash collision and how to solve it?
A: as long as the array index values calculated by two key s are the same, hash collision will occur. jdk8 previously used linked lists to resolve hash collisions. jdk8 then uses linked list + red black tree to solve hash collision.
3.5 how to store key value pairs if the hashcodes of two keys are the same?
A: compare whether the contents are the same through equals. Similarly, the new value will overwrite the old value, otherwise the new key value pair will be added to the hash table.
3.6 why does the number of nodes in the HashMap bucket exceed 8 before turning into a red black tree?
- Answer one
In the case of good hashCode dispersion, the probability of using tree bin is very small, because the data is evenly distributed in each bin, and the length of the linked list in almost no bin will reach the threshold (8). However, under the random hashCode, the discreteness may become worse. However, JDK can not prevent users from implementing this bad hash algorithm, so it may lead to uneven data distribution.
In fact, the distribution frequency of all bin nodes under the random hashCode algorithm follows the following Poisson distribution.
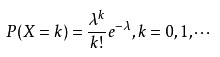
When the expansion threshold is 0.75, (even if the variance is large due to expansion), the parameter average is followed λ= Poisson distribution of 0.5. You can see the following calculation probability. The probability that the length of the linked list in a bin reaches 8 elements is 0.00000006, which is almost an impossible event.0: 0.60653066 1: 0.30326533 2: 0.07581633 3: 0.01263606 4: 0.00157952 5: 0.00015795 6: 0.00001316 7: 0.00000094 8: 0.00000006 more: less than 1 in ten million
- Answer two
The average lookup length of the red black tree is log(n). If the length is 8, the average lookup length is log(8) = 3. The average search length of the linked list is n/2. When the length is 8, the average search length is 8 / 2 = 4, which is necessary to convert into a tree; If the length of the linked list is less than or equal to 6, 6 / 2 = 3, and log(6) = 2.6, although the speed is also very fast, the time to convert into tree structure and generate tree will not be too short.