Recover the binary tree according to traversal

In the knowledge of binary tree, finding or traversing binary tree is a very important knowledge point. Because the author only paid attention to the traversal process of binary tree before, but ignored the importance of the inverse process of recovering binary tree from traversal. When I saw an algorithm problem one day, I found that there was still an inverse process in the former, middle and later traversal! So I opened the corresponding books and wrote this note in combination with the algorithm title
Theorem 1: the preorder traversal and inorder traversal of any binary tree can uniquely determine the binary tree

In fact, this may be a little confusing. Let me explain my idea. The middle order traversal order of binary tree is left root right, and the first order traversal order is root left right. In this order, the first node of the first order traversal must be the root node, the root node of the middle order traversal must be in the middle, and the left and right sides are the middle order traversal of the left and right subtrees respectively, According to the node distribution at the middle order traversal root node position, a binary tree can be restored by recursion. The recursive steps of each step can be
1 , first before look for reach in order Times calendar root section spot of position Set 2 , in order Times calendar root section spot Left edge of ( common k individual ) number according to by root section spot Left son tree of in order Times calendar 3 , right edge of ( n − k − 1 individual ) number according to by root section spot right son tree of in order Times calendar 1. First, find the location of the middle order traversal root node \ \ 2. The data on the left (K in total) of the middle order traversal root node is the middle order traversal of the left subtree of the root node \ \ 3. The data on the right (n-k-1) is the middle order traversal of the right subtree of the root node 1. First, find the location of the middle order traversal root node. 2. The data on the left (k in total) of the middle order traversal root node is the middle order traversal of the left subtree of the root node. 3. The data on the right (n − k − 1) is the middle order traversal of the right subtree of the root node
Split the problem into subtrees, and the subtree is split into subtrees. Recurse layer by layer and backtrack in turn until the final result is returned. Here you can draw a diagram to understand the allocation process. For example, the middle order traversal and first order traversal of a tree are respectively:

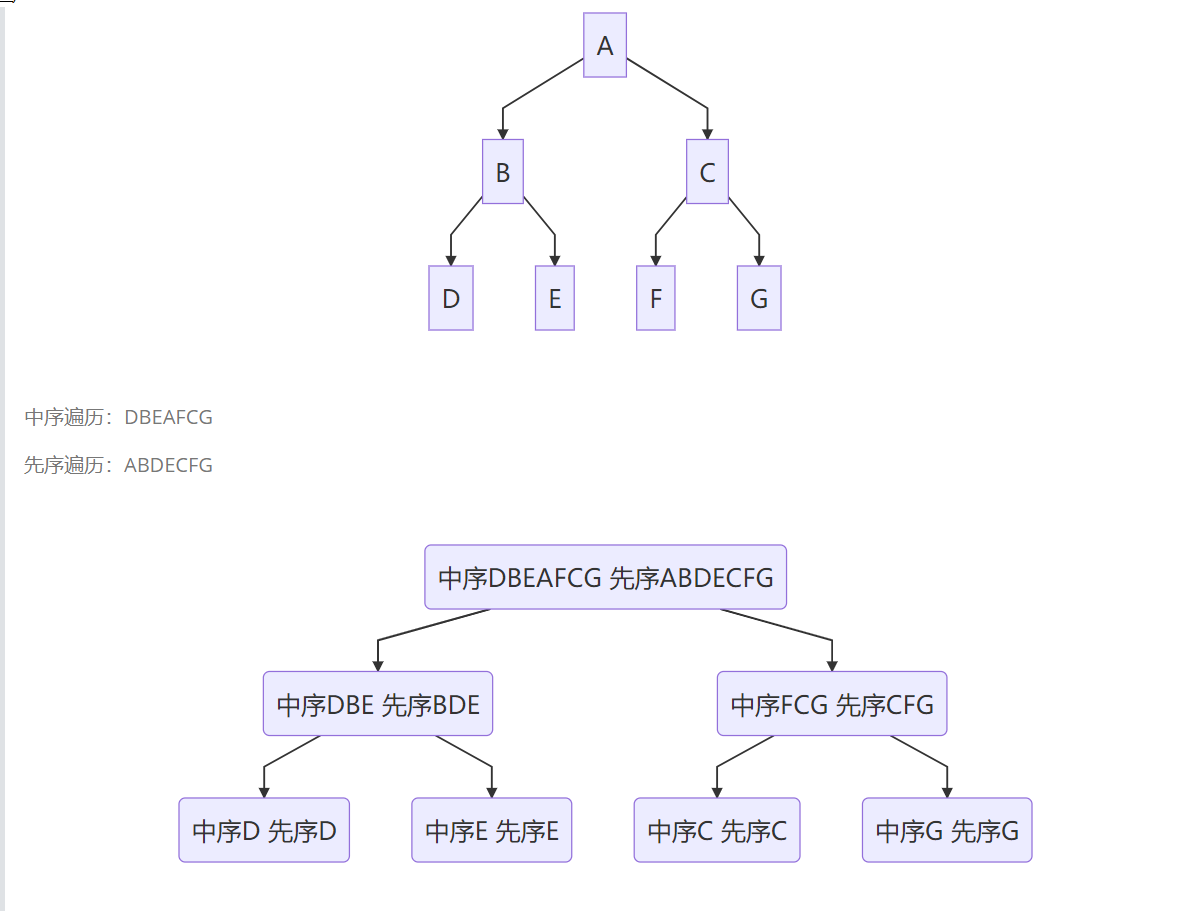
See code:

typedef struct node{
    char data;
    node* left;
    node* right;
} BTNode; //The node data organization type of binary tree adopts the binary chain storage structure, and the binary tree is also restored from post order traversal and middle order traversal
BTNode* CreateBT1(char* pre,char *in,int n){
    BTNode* b;
    char *p;
    int k;
    if(n<=0)
        return nullptr;
    b = (BTNode*)malloc(sizeof(BTNode));
    b->data = *pre;
    for(p = in;p<in+n;p++){
        if(*p==*pre)
            break;
    }
    k = p - in;
    b->left = CreateBT1(pre+1,in,k);
    b->right = CreateBT1(pre+k+1,p+1,n-k-1);
}
//Here, it is assumed that the element stored in the binary tree is char

leedCode also has the same algorithm problem and the same idea. Its title is

According to the preorder traversal and inorder traversal of a tree, a binary tree is constructed.

be careful:
You can assume that there are no duplicate elements in the tree.

For example, give

preorder = [3,9,20,15,7]
Middle order traversal inorder = [9,3,15,20,7]
Return the following binary tree:

3
/ \
9 20
/ \
15 7
Source: LeetCode
Link: https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

Code (c + + implementation)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        TreeNode* roots = nullptr;
        if(preorder.size()!=inorder.size())  //Ensure that the array length of the incoming pre traversal and subsequent traversal is the same
            return roots;
        if(preorder.size()<=0) //Ensure that the passed in array length is valid
            return roots;
        roots = buildTree(preorder,inorder,0,preorder.size()-1,0,inorder.size()-1); //The values of roots are assigned recursively
        return roots;
    }
    TreeNode* buildTree(vector<int>& preorder,vector<int>& inorder,int pre_start,int pre_end,int in_start,int in_end){
        TreeNode* roots = new TreeNode(); //Initialize the node of a tree
        roots->val = preorder[pre_start]; //The first value of the first traversal array is the value of the root node
        int k = in_start; //Starting from the starting point of the middle order traversal, find the location of the root node in the middle order traversal
        for(;k<in_end;k++){
            if(preorder[pre_start]==inorder[k])
                break; //Find the location of the root node in the middle order traversal
        } 
        if(pre_end==pre_start){ //If the start position and end position are the same, there is only one node in the preorder array in the description, and there is no need to assign values to the left and right subtrees
            return roots;
        }else{  //There are three situations          
            if(k==in_start){ //If this root node has no left subtree, the root node is at the front of the middle order traversal
                roots->right = buildTree(preorder,inorder,pre_start+1,pre_end,k+1,in_end);
            }else if(k==in_end){ //This root node has no right subtree, and the root node appears at the end of the middle order traversal
                roots->left = buildTree(preorder,inorder,pre_start+1,pre_end,in_start,k-1);
            }else{ //There are both left subtree and right subtree
                roots->left = buildTree(preorder,inorder,pre_start+1,pre_start+k-in_start,in_start,k-1);
                roots->right = buildTree(preorder,inorder,pre_start+k-in_start+1,pre_end,k+1,in_end);
            }
        }
        return roots;
    }
};

Java implementation

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        TreeNode roots = new TreeNode();
        if(preorder.length!=inorder.length)
            return roots;
        if(preorder.length<=0)
            return roots;
        roots = buildTree(preorder,inorder,0,(preorder.length-1),0,(inorder.length-1));
        return roots;
    }

    private TreeNode buildTree(int[] preorder,int[] inorder,int pre_start,int pre_end,int in_start,int in_end){
        TreeNode roots = new TreeNode();
        roots.val = preorder[pre_start];
        int k = in_start;
        for(;k<in_end;k++){
            if(preorder[pre_start]==inorder[k])
                break;
        }
        if(pre_start==pre_end)
            return roots;
        else{
            if(k==in_start)
                roots.right = buildTree(preorder,inorder,pre_start+1,pre_end,k+1,in_end);
            else if(k==in_end)
                roots.left = buildTree(preorder,inorder,pre_start+1,pre_end,in_start,k-1);
            else{
                roots.left = buildTree(preorder,inorder,pre_start+1,pre_start+k-in_start,in_start,k-1);
                roots.right = buildTree(preorder,inorder,pre_start+k-in_start+1,pre_end,k+1,in_end);
            }
        }    
        return roots;
    }
}

Theorem 2: the middle order traversal and post order traversal of any binary tree can uniquely determine the binary tree

After understanding the above idea of recovering a binary tree from preorder traversal and middle order traversal, the same idea is used to recover a binary tree from post order traversal and middle order traversal, but the order will change a little, because the root node of post order traversal is at the end. At this time, we need to start from the end of post order traversal to find the location of the root node in middle order traversal, If a binary tree is only understood as the root node and the left and right subtrees, its post order traversal can be understood as the post order traversal of the left subtree + the post order traversal of the right subtree + the root node, and the middle order traversal, that is, the above-mentioned middle order traversal of the left subtree + the root node + the middle order traversal of the right subtree. In this way, the corresponding part can be split, Another subproblem with simplified thinking logic is obtained!, According to this idea, you can also draw the flow chart of the tree above through traversal and recovery in the middle and later order

Middle order traversal: DBEAFCG

Post order traversal: DEBFGCA

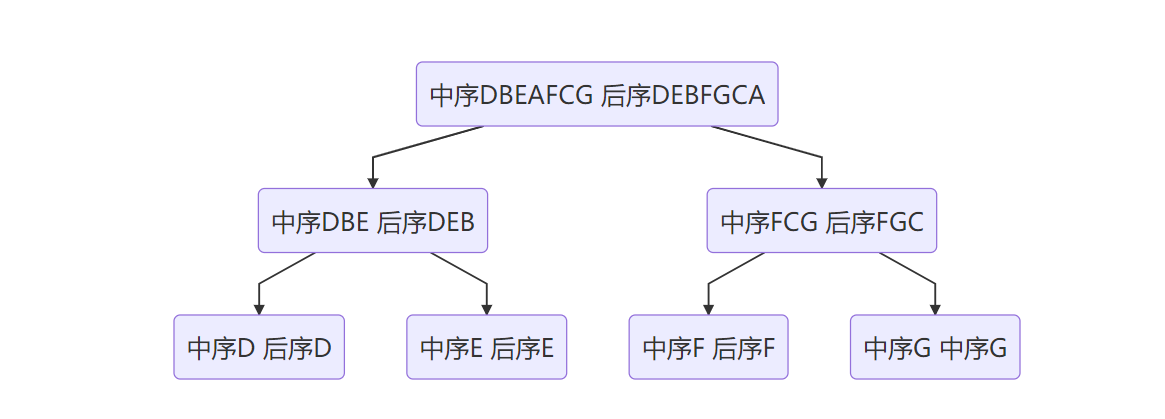
BTNode* CreateBT2(char *post,char *in,int n){
    BTNode *b;
    char r,*p;
    int k;
    r = *(post+n-1);
    b = (BTNode*)malloc(sizeof(BTNode));
    b->data = r;
    for(p = in;p<in+n;p++){
        if(*p==r)
            break;
    }
    k = p-in;
    b->left = CreateBT2(post,in,k);
    b->right = CreateBT2(post+k,p+1,n-k-1);
}