1 Basic Concepts

▪ Nonlinear time comparison sort: the relative order between elements is determined by comparison. Because its time complexity cannot exceed O(nlogn), it is called nonlinear time comparison sort sort. 　
▪ Linear time non comparison sort: it does not determine the relative order between elements through comparison. It can break through the time lower bound based on comparison sort and run in linear time. Therefore, it is called linear time non comparison sort.

2 bubble sorting

2.1 basic ideas

▪ Compare adjacent elements. If the first one is bigger than the second, exchange them.
▪ Do the same for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end. At this point, the last element should be the largest number.
▪ Repeat the above steps for all elements except the last one.
▪ Continue to repeat the above steps for fewer and fewer elements at a time until no pair of numbers need to be compared.

2.2 code representation

public static void main(String[] args) {
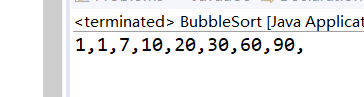
		int [] arr= {1,10,20,30,1,90,7,60};
		bubblesort(arr);
//		bubblesort2(arr);
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i]+",");
		}
	}
//Large number floating
	public static void bubblesort(int[] arr) {
		for (int i = 0; i < arr.length-1; i++) {
			for (int j = 0; j < arr.length-1-i; j++) {
				if(arr[j]>arr[j+1]) {
					swap(arr,j,j+1);
				}
			}
		}
		
	}
	//Decimal sinking
	public static void bubblesort2(int[] arr) {
		for (int i = 0; i < arr.length-1; i++) {
			for (int j =arr.length-1; j>i; j--) {
				if(arr[j]<arr[j-1]) {
					swap(arr,j,j-1);
				}
			}
		}
		
	}
	//Exchange data
private static void swap(int[] arr,int i,int j) {
		arr[i] = arr[i] + arr[j];
		 arr[j] = arr[i] - arr[j];
		 arr[i] = arr[i] - arr[j];
	}
}

result

3 select sort

3.1 basic ideas

▪ First, find the smallest (large) element in the unordered sequence and store it at the beginning of the sorted sequence.
▪ Then continue to find the smallest (large) element from the remaining unordered elements, and then put it at the end of the sorted sequence.
▪ Repeat step 2 until all elements are sorted.

3.2 code representation

public static void main(String[] args) {
		int [] arr= {20,10,20,30,1,90,7,60};
		jiaohuan(arr);
//		xiaoshu(arr);
//		jiaohuan01(arr);
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i]+",");
		}
	}
	//Select sort
	private static void jiaohuan01(int[] arr) {
		for (int i = 0; i < arr.length; i++) {
			 int min =i;
			 for (int j = i; j < arr.length; j++) {
				if(arr[min]>arr[j]) {
					min=j;
				}
			}
			 if(min!=i) {
				 zhuanhuan(arr,i,min);
			 }
		}
	}
	//Data exchange
	private static void zhuanhuan(int[] arr,int i,int j) {
		arr[i] = arr[i] + arr[j];
		 arr[j] = arr[i] - arr[j];
		 arr[i] = arr[i] - arr[j];
	}

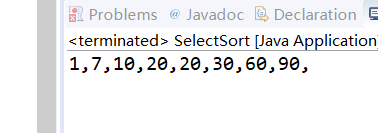
result

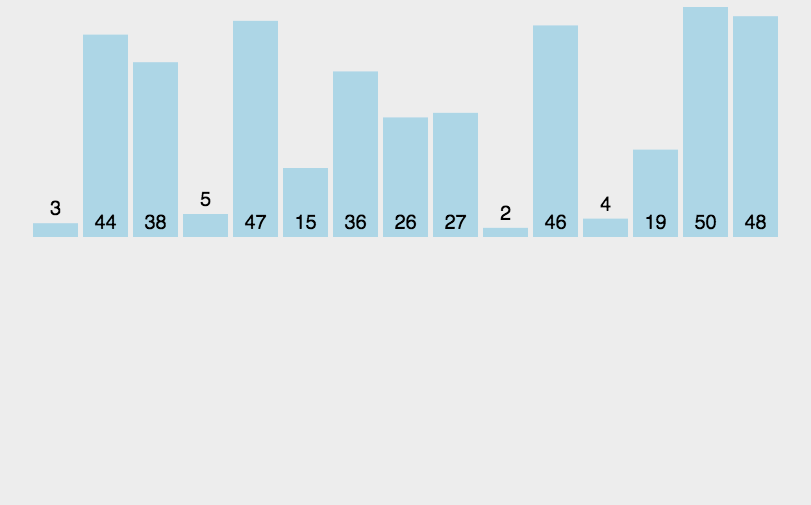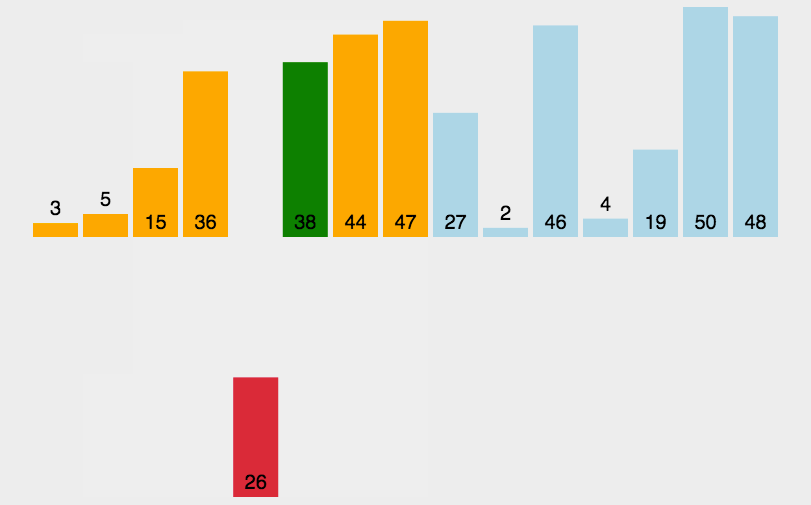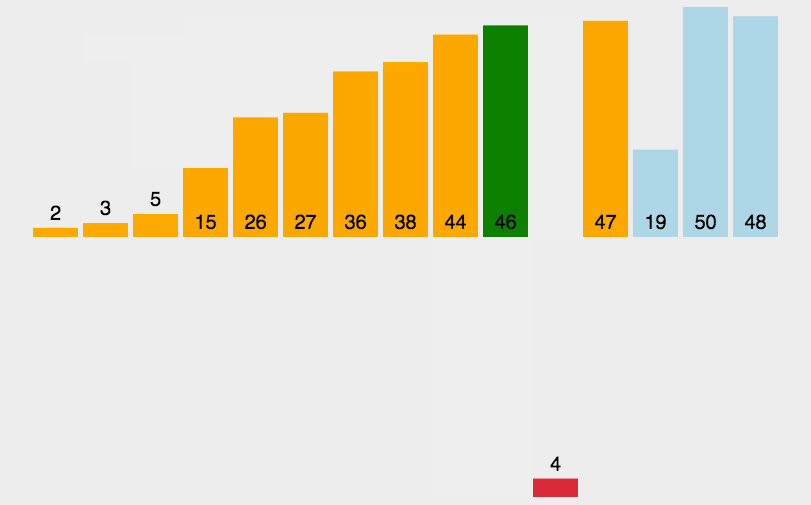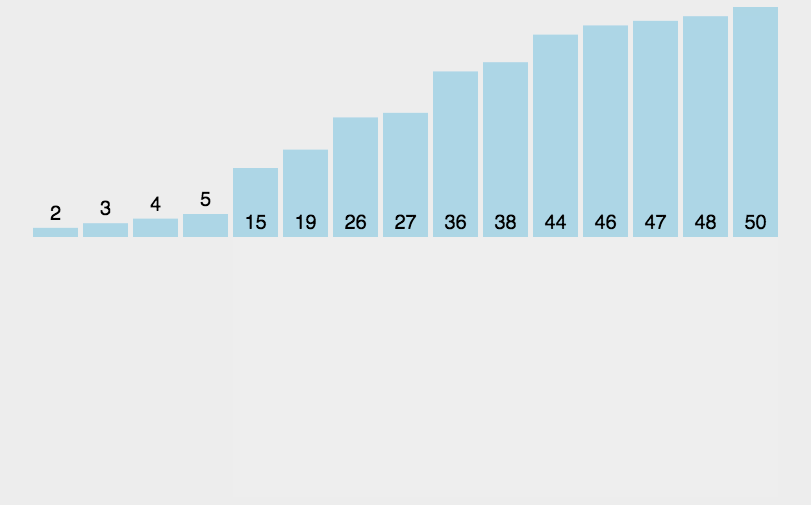
4 insert sort

4.1 basic ideas

▪ Insert sort works like many people sort a hand of playing cards. At first, our left hand is empty and the cards on the table face down. Then, we take a card from the table one at a time and insert it in the correct position in our left hand. In order to find the correct position of a card, we compare it from right to left with each card already in hand. The cards on the left hand are always sorted. It turns out that these cards are the top cards in the pile on the table.
▪ Insertion sorting means that in the elements to be sorted, assuming that the first n-1 (where n > = 2) numbers are already in good order, insert the nth number into the previously arranged sequence, and then find the appropriate position so that the sequence of inserting the nth number is also in good order. According to this method, all elements are inserted until the whole sequence is ordered, which is called insertion sorting.

4.2 code representation

public static void main(String[] args) {
		int [] arr= {1,10,20,30,1,90,7,60};	
		insertSort(arr);
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i]+",");
		}

	}
	private static void insertSort(int [] arr) {
		for (int i = 1; i < arr.length; i++) {
			for (int j = i; j > 0 && arr[j] < arr[j - 1] ; j--) {
				swap(arr, j, j - 1);
			}
		}
	}
	
	//Data exchange
	private static void swap(int[] arr,int i,int j) {
		arr[i] = arr[i] + arr[j];
		 arr[j] = arr[i] - arr[j];
		 arr[i] = arr[i] - arr[j];
	}
}

result