What is a segment tree

Segment tree is a binary search tree. With the idea of divide and conquer algorithm, it divides an interval into some unit intervals, and each unit interval corresponds to a leaf node in the segment tree----------------- Adapted from Baidu Encyclopedia

Function of line segment tree

Question: Here you are n n n unordered numbers, q q q operations, asking for a certain interval [ l , r ] [l, r] The sum of [l,r] or modify the value of this interval. assume 1 < = n , q < = 100 , 000 1 <= n, q <= 100,000 1 < = n, Q < = 100000, the time limit for you is 1 s 1s 1s.
If violence is used? It is assumed that the interval of each modification and query is [ 1 , n ] [1, n] [1,n], then the worst time complexity needs O ( q ∗ n ) O(q*n) O(q * n), obviously timeout.
At this time, we need to use the magical line segment tree.

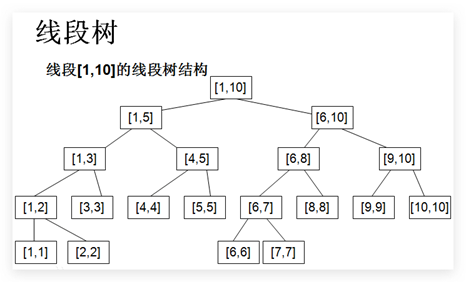
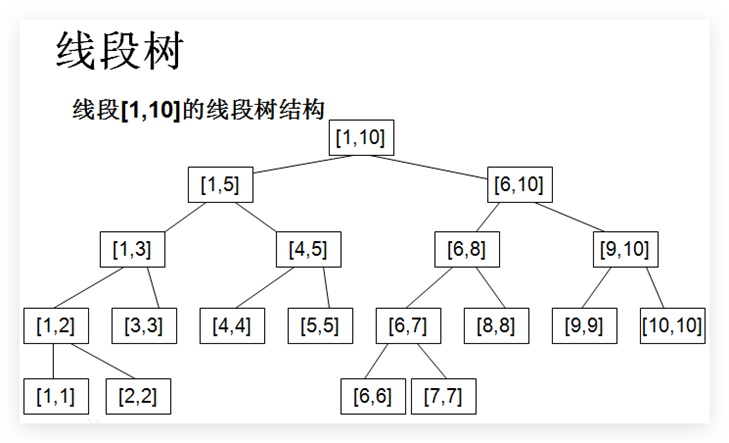
Observe its structure:

Achievements:

By observing the law of node subscript, it can be concluded that the subscripts of the two son nodes of the current node p are p ∗ 2 p*2 p * 2 and p ∗ 2 + 1 p*2 +1 p∗2+1.
Recursive tree building is similar to merge sorting. Time complexity O ( n ∗ l o g 2 ( n ) ) O (n*log2(n)) O(n∗log2(n))

void build(int l, int r, int p){
	if(l ==r){
		tree [p] = a[l]; //Leaf node information
		return ;
	}
	int mid = (l + r) >> 1;	// Equivalent to mid = (l + r) / 2,
	build(l, mid, p << 1); //Left bound interval
	build(mid + i, r, p << 1|1); //In the right section, P < 1 | 1 is equivalent to p / 2 + 1
	tree[p] = tree[p << 1] + tree[p << 1|1]; //Upload son node information
}

Query the information of interval [L,R]:

Assume that every time you access a node p p p is an interval [ l , r ] [l, r] [l,r], m i d = ( l + r ) / 2 mid = (l + r)/ 2 mid=(l+r)/2
If [ l , r ] [l, r] [l,r] happens to be [ L , R ] [L,R] [L,R] contains (i.e L ≤ l L≤l L≤l && r ≤ R ) r ≤ R) r ≤ R), then p p We all need the information of node p.
In other cases, judgment is required m i d mid mid and L , R L,R 50. Relationship of R:
1. If L ≤ m i d L ≤ mid L ≤ mid, indicating that we need some information of its left interval.
2. If R > m i d R > mid R> Mid, indicating that we need some information of its right interval· Finally, all the information sets of the above situations are returned.

int query(int l, int r, int p, int L, int R){
	if (L <= l && r <= R) return tree[p]; //If the interval contains, all information of the node will be returned
	int mid = (l + r) >> 1, ret = 0;// ret is used to save information
	if (L <= mid) ret += query(l, mid, p << 1, L, R);//Take part of the information of the left section
	if (R > mid) ret += query(mid + 1, r, p << 1|1，L, R);//Take part of the information of the right section
	return ret;//Return the above results
}

To modify a location k's information:

Very simple, just find and modify the information of the corresponding leaf node.

void update(int l, int r, int p, int k, int s) {
	if(l == r){
		tree[p] = s;
		return ;
	}
	int mid = (l + r) >> 1;
	if(k <= mid) update(l, mid, p << 1, k, s); // k < = mid indicates that k is in the left interval
	else update(mid + 1, r, p << 1 | 1，k, s); // Otherwise, it is in the right interval
	tree[p] = tree[p << 1]+ tree[p << 1|1]; // Don't forget to update the information of the p node~
}

The time complexity is O ( l o g 2 ( n ) ) O(log2(n)) O(log2(n))

Modify interval [L,R]

Here's the problem. What if the interval [L,R] modifies the information?
Continue the idea of violence, [L,R] one by one.
Then the time complexity of one modification is O ( n ∗ l o g 2 ( n ) ) O(n*log2(n)) O(n * log2(n)), modified q q q times
Time complexity up to O ( q ∗ n ∗ l o g 2 ( n ) ) O (q*n*log2(n)) O(q * n * log2(n)), but not as simple violence?
Can it be converted into query time complexity?
That is, we only need to modify the nodes that can be queried by interval query.
For example, total interval [ 1 , 10 ] [1,10] [1,10], to modify [ 4 , 9 ] [4,9] [4,9] interval, we only need to modify it [ 4 , 5 ] [4,5] [4,5], [ 6 , 8 ] [6,8] [6,8], [ 9 , 9 ] [9,9] The information of the node where [9,9] is located.
What about the child nodes of these nodes?
The modified interval is marked with lazy. If the sub interval of this interval is accessed next time, this mark will be lowered.

Magic lazy tag for interval modification. Time complexity optimized to O ( l o g 2 ( n ) ) O(log2(n)) O(log2(n))

void update(int l, int r,int p, int L, int R, int s) {
	if(L <= l && r <= R) { //If the current access interval is included in the interval to be accessed
		tree[p] += (r - l + 1) * s; //First, update the value of the current node
		lazy[p] += s; //Label with lazy
		return ;
	}
	int mid = (l + r) >> 1;
	if(lazy[p] != 0){ //If the current interval is marked with lazy, it needs to be lowered
		tree[p << 1] += (mid - l + 1) * lazy[p];
		tree[p << 1 | 1] += (r - mid) * lazy[p];  
		//First update the values of the two child nodes
		lazy[p << 1] += lazy[p];
		lazy[p << 1 | 1] += lazy[p]; 
		//Drop tag to two child nodes
		lazy[p] = 0; //The current node is unmarked
	}
	if(L <= mid) update(l, mid, p << 1, L, R, s);
	// L < = mid indicates that the left interval needs to be updated
	if(R > mid)update(mid + 1, r, p << 1 | 1，L，R, s);
	// R > mid indicates that the right interval needs to be updated
	tree[p] = tree[p << 1] + tree[p << 1|1];
	// Don't forget to update the information of the p node
}

Magic lazy tag for interval modification. Time complexity optimized to O ( l o g 2 ( n ) ) O (log2(n)) O(log2(n))

int query (int l, int r, int p, int L, int R){
	if(L <= l && r <= R) return tree[p];
	// If the interval contains, all information of the node will be returned
	int mid = (l + r) >> 1, ret = 0; // ret is used to save information
	if(lazy [p] != 0) {
	//If the current interval is marked with lazy, it needs to be lowered
		tree[p << 1] += (mid - l + 1) * lazy[p];
		tree[p << 1|1] += (r - mid) * lazy[p];//First update the values of the two child nodes
		lazy[p << 1] += lazy[p];
		lazy[p << 1|1] += lazy[p];//Drop tag to two child nodes
		lazy[p] = 0;//The current node is unmarked
	}
	if(L <= mid) ret += query(l, mid, p << 1, L, R);
	//Take part of the information of the left section
	if(R > mid) ret += query(mid + 1, r, p << 1|1, L,R);
	//Take part of the information of the right section
	return ret;//Return the above results
}

Summary & Precautions:

Tree building time complexity O ( n ∗ l o g 2 ( n ) ) O (n*log2(n)) O(n∗log2(n))
Single point / interval update / query time complexity O ( l o g 2 ( n ) ) O(log2(n)) O(log2(n))
The time complexity is extremely excellent, and the space needs to be opened 4 ∗ n 4* n 4∗n
It is used to process some interval queries and modifications that require divisible interval information