//Updated on January 22, 2022
The updated content is mainly the introduction classic of algorithm competition - Training Guide (upgraded version) (edited by Liu Rujia and Chen Feng), Chapter 4 geometric problems
1 basis of 2D geometry
In the plane coordinate system, vectors, like points, are also represented by two numbers x and y. Chapter 6 introduces the concept of homogeneous coordinates, so as to distinguish open points and vectors in the program. The following points and vectors are represented by two numbers x and y.
Don't confuse points with vectors. There are the following points - point = vector, vector + vector = vector, vector - vector = vector, point + vector = point, and point + point is meaningless.
struct Point{
double x,y;
Point(double x=0, double y=0):x(x),y(y) { } // Constructor to facilitate code writing
};
typedef Point Vector; // In terms of program implementation, Vector is only an alias of Point
//Vector + vector = vector, point + vector = point
Vector operator + (Vector A, Vector B) { return Vector(A.x+B.x, A.y+B.y); }
//Point point = vector
Vector operator - (Point A, Point B) { return Vector(A.x-B.x, A.y-B.y); }
//Vector * number = vector
Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }
//Vector / number = vector
Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); }
bool operator < (const Point& a, const Point& b) {
return a.x<b.x || ( a.x == b.x && a.y < b.y);
}
const double eps = 1e-10;
int dcmp(double x){
if(fabs(x) < eps) return 0; else return x < 0 ? -1 : 1;
}
bool operator == (const Point& a, const Point& b){
return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0;
}Note that the above "equality" function uses the "three state function" dcmp to reduce the accuracy problem.
Polar angle:
Polar angle of vector: the angle required to rotate from the positive half axis of x axis to the direction of the vector.
C standard library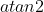
Function is used to find the polar angle. For example, the polar angle of vector (x,y) is
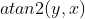(in radians).
//Examples of polar function atan2() function
#include<bits/stdc++.h>
using namespace std;
struct Point{
double x,y;
Point(double x=0, double y=0):x(x),y(y) { } // Constructor to facilitate code writing
};
typedef Point Vector; // In terms of program implementation, Vector is only an alias of Point
int main(){
ios::sync_with_stdio(false);
double x,y,Polar_angle; Vector vec;
cin>>x>>y;
vec=Vector(x,y);
Polar_angle=atan2(y,x);
cout<<Polar_angle<<endl;
return 0;
}
/*
#1 #2 #3
0 1 -1 0 13 34
1.5708 3.14159 1.20559
*/1.1 basic operation
| Dot product |
| Cross product |
| Positional relationship between two vectors |
| Vector rotation |
| Geometric calculation based on complex number |
Dot product: the dot product of two vectors v and w is equal to the product of their lengths and multiplied by their angle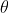
Cosine of. Among them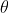It refers to the angle of counterclockwise rotation from v to w, so when the included angle is greater than 90 degrees, the dot product is negative.
The cosine is an even function, so the dot product satisfies the commutative law. If two vectors are perpendicular, the dot product is equal to 0. It is not difficult to deduce: in the plane coordinate system, two vectors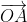
and
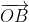The dot product of is equal to
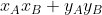. The calculation method of point product and the function of using point product to calculate the length and included angle of vector are given here. The code is as follows:
struct Point{
double x,y;
Point(double x=0, double y=0):x(x),y(y) { } // Constructor to facilitate code writing
};
typedef Point Vector; // In terms of program implementation, Vector is only an alias of Point
double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A, A)); }
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }//2022/01/23
Cross product: simply put, the cross product of two vectors v and w is equal to twice the directed area of the triangle composed of v and w. It is not difficult to find that the cross product does not satisfy the commutative law. in fact,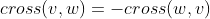
. In the coordinate system, two vectors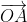and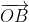The cross product of is equal to
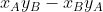. The code is as follows:
struct Point{
double x,y;
Point(double x=0, double y=0):x(x),y(y) { } // Constructor to facilitate code writing
};
typedef Point Vector; // In terms of program implementation, Vector is only an alias of Point
//Point point = vector
Vector operator - (Point A, Point B) { return Vector(A.x-B.x, A.y-B.y); }
double Cross(Vector A, Vector B){ return A.x*B.y-A.y*B.x; }
double Area2(Point A, Point B, Piont C){ return Cross(B-A, C-A); }Positional relationship of two vectors: by combining cross product and dot product, we can judge the positional relationship of two vectors in more detail.
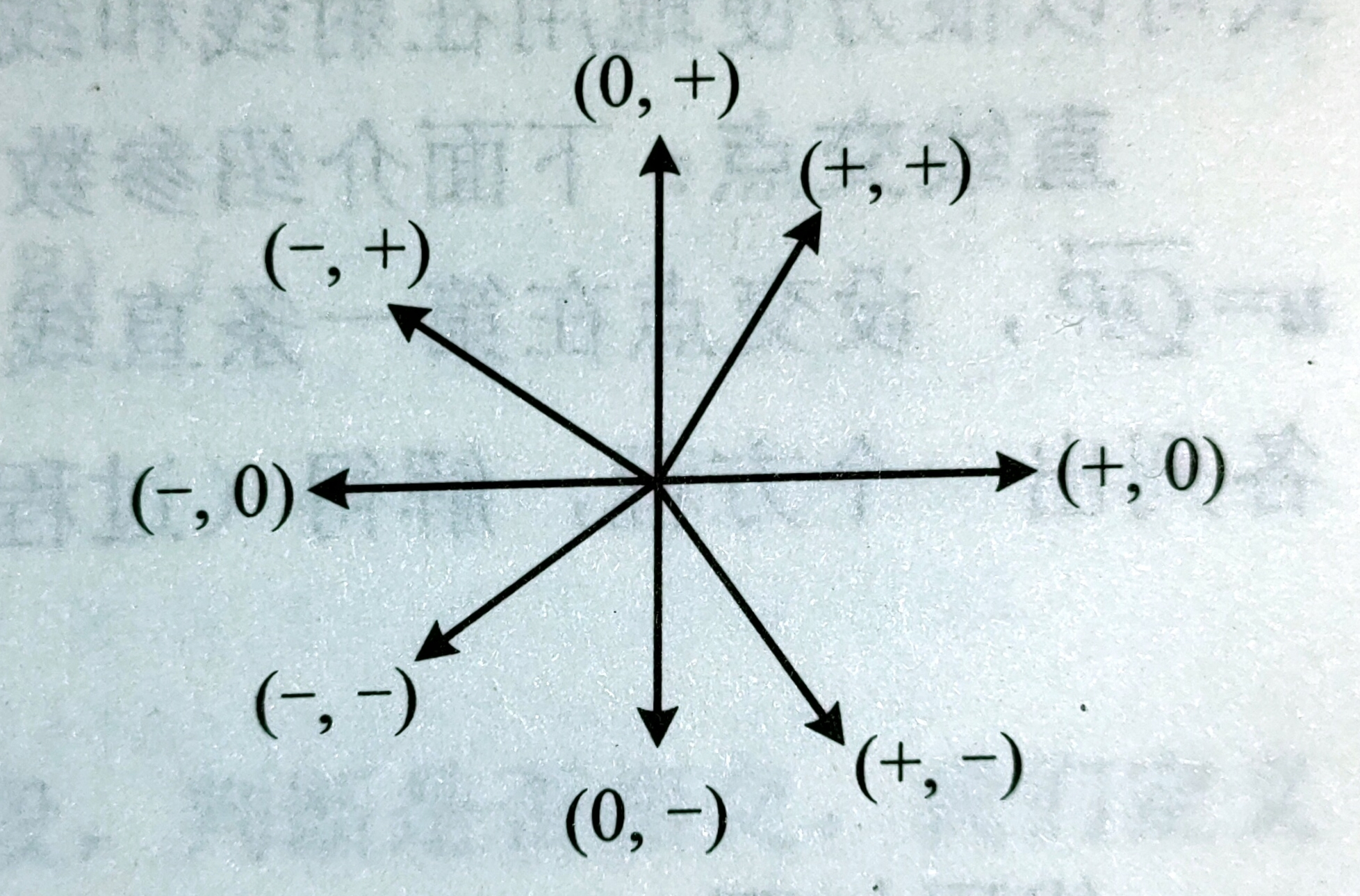
As shown in the figure, the first number in brackets is the symbol of dot product, and the second number is the symbol of cross product. The first vector v is always horizontal to the right, and various situations of the other vector w are included in the figure above. For example, when the end point of W is in the second image limit at the upper left, the dot product is negative, but the cross product is positive, which is represented by (-, +).
Vector rotation: the vector can rotate around the starting point. The formula is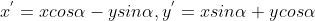
, where
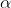Is the angle of counterclockwise rotation. The code is as follows:
//rad is radian
Vector Rotate(Vector A, double rad){
return Vector(A.x*cos(rad)-A.y*sin(rad), A.x*sin(rad)+A.y*cos(rad));
} Special case: the following function is used to calculate the unit normal of the vector, that is, turn left 90 degrees and normalize the length.
//Make sure A is not A zero vector before calling
Vector Normal(Vector A){
double L=Length(A);
return Vector(-A.y/L, A.x/L);
} Geometric calculation based on complex numbers: the method of using complex numbers in C + + to realize points and vectors. After the following definition, we automatically have the constructor, addition and subtraction and quantity product. Use real(p) and imag(p) to access the real part and imaginary part, and conj(p) returns the conjugate complex number, i.e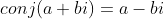
. Relevant codes are as follows:
#include<complex>
using namespace std;
typedef complex<double> Point;
typedef Point Vector;
double Dot(Vector A, Vector B){ return real(conj(A)*B); }
double Cross(Vector A, Vector B){ return imag(conj(A)*B); }
Vector Rotate(Vector A, double rad){ return A*exp(Point(0, rad)); }The efficiency of the above function is not very high, but it is quite convenient and easy to remember.
1.2} points and straight lines
| Parametric representation of lines |
| Line intersection |
| Distance from point to line |
| Distance from point to line segment |
| Projection of point on line |
| Line segment intersection determination |
Parametric representation of the line:
Formula: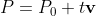
(P0 is a point on the line, v is the direction vector, t is the parameter). If two different points a and B on the line are known, the direction vector is B-A, so the parameter equation is
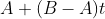. The most convenient part of the parametric equation is that the equation forms of straight line, ray and line segment are the same, and the difference is only the parameter t.
| type | t range |
| straight line | No scope restrictions |
| radial |  |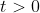
| line segment |  |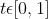
Line intersection: set the lines as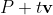
and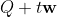
, set vector
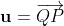, let the parameter of the intersection point on the first straight line be
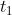, the parameter on the second line is
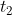, then the x and y coordinates can each list an equation, and the solution is:
， 
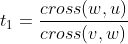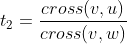. The code is as follows:
//Before calling, please ensure that the two straight lines P+tv and Q+tw have a unique intersection if and only if Cross(v,w) is not 0
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w){
Vector u = P-Q;
double t = Cross(w, u) / Cross(v, w);
return P+v*t;
} It should be noted that from the above formula, if all components of P, V, Q and W are rational numbers, the intersection coordinates are also rational numbers. In the case of high precision requirements, you can consider customizing the score class. (？？？)
Distance from point to line segment: there are two possibilities for the distance from point to line segment. Set the projection point as Q.
① If Q is on line AB, the distance is the distance from point P to line ab.
② If Q is not on segment AB, there are two cases:
1) If Q is on ray BA, the calculated distance is PA distance;
2) If Q is on ray AB, the calculated distance is PB distance.
The position of Q can be judged by dot product. The code is as follows:
double DistanceToSegment(Point P, Point A, Point B){
if(A == B) return Length(P-A);
Vector v1 = B - A, v2 = P - A, v3 = P - B;
if(dcmp(Dot(v1, v2)) < 0) return Length(v2);
else if(dcmp(Dot(v1, v3)) > 0) return Length(v3);
else return fabs(Cross(v1, v2)) / Length(v1);
}Projection of point on a straight line: in order to find the above projection point Q, we write the straight line AB as a parametric formula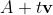
(v is vector)
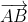)And let the parameter of Q be
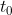, then
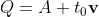. According to PQ perpendicular to AB, the dot product of the two vectors should be 0, so
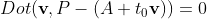. According to the law of distribution
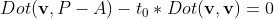, so we can solve it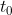To get the Q point. The code is as follows:
Point GetLineProjection(Point P, Point A, Point B){
Vector v = B-A;
return A+v*(Dot(v, P-A) / Dot(v, v) );
}Line segment intersection determination: that is, given two line segments, judge whether they intersect.
We define "normal intersection" as that two line segments have exactly one common point, and the common point is not the endpoint of any line segment. (it can be understood that both line segments do not contain endpoints)
The necessary and sufficient condition for the normal intersection of line segments is that the two endpoints of each line segment are on both sides of the other line segment (the "two sides" here are different symbols of the cross product). The code is as follows:
bool SegmentProperIntersection(Point a1, Point a2, Point b1, Point b2){
double c1 = Cross(a2-a1,b1-a1), c2 = Cross(a2-a1,b2-b1);
c2 = Cross(b2-b1,a1-b1), c4 = Cross(b2-b1,a2-b1);
return dcmp(c1)*dcmp(c2)<0 && dcmp(c3)*dcmp(c4)<0;
}The situation is more complicated if intersection at the end is allowed:
If both c1 and c2 are 0, it means that the two line segments are collinear, and there may be partial overlap at this time;
If c1 and c2 are not both 0, there is only one intersection method, that is, one endpoint is on another segment.
In order to judge whether the above situation occurs, it is also necessary to judge whether a point is on a line segment (excluding the endpoint). The code is as follows:
bool OnSegment(Point p, Point a1, Point a2){
return dcmp(Cross(a1-p, a2-p)) == 0 && dcmp(Dot(a1-p, a2-p) < 0);
}1.3 polygon
Calculate the directed area of a polygon
① Convex polygon can be divided into n-2 triangles from the first vertex, and then add up the area. The code is as follows
double ConvexPolygonArea(Point* p, int n){
double area = 0;
for(int i = 1; i < n-1; i++)
area += Cross(p[i]-p[0], p[i+1]-p[0]);
return area/2;
}② For non convex polygons, the above method is also applicable to non convex polygons. Since the area of the triangle is directed, the outer part can be offset by positive and negative. In fact, it can be divided from any point.
The point p[0] can be taken as the dividing vertex. On the one hand, it can reduce two cross products (the cross product of 0 and any vector is equal to 0), on the other hand, it also reduces the possibility of multiplication overflow without special treatment (when i=n-1, the next vertex is p[0] instead of p[n], because p[n] does not exist). The code is as follows:
//Directed area of polygon
double PolygonArea(Point* p, int n){
double area = 0;
for(int i = 1; i < n-1; i++)
area += Cross(p[i]-p[0], p[i+1]-p[0]);
return area/2;
} You can also take the coordinate origin as the dividing point to reduce the number of multiplication, and the code needs to be written by yourself.
// 2022/01/25
1.4} selected examples
1. UVA11178 Morley's Theorem(Morley theorem)
#include<bits/stdc++.h>
using namespace std;
struct Point{
double x,y;
Point(double x=0, double y=0):x(x),y(y) { }
};
typedef Point Vector;
Vector operator + (Vector A, Vector B) { return Vector(A.x+B.x, A.y+B.y); }
Vector operator - (Point A, Point B) { return Vector(A.x-B.x, A.y-B.y); }
Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }
Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); }
double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A, A)); }
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }
double Cross(Vector A, Vector B){ return A.x*B.y-A.y*B.x; }
Vector Rotate(Vector A, double rad){
return Vector(A.x*cos(rad)-A.y*sin(rad), A.x*sin(rad)+A.y*cos(rad));
}
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w){
Vector u = P-Q;
double t = Cross(w, u) / Cross(v, w);
return P+v*t;
}
Point read_point(){
Point p;
scanf("%lf %lf",&p.x,&p.y);
return p;
}
Point getD(Point A, Point B, Point C){
Vector v1 = C-B;
double a1 = Angle(A-B, v1);
v1 = Rotate(v1, a1/3);
Vector v2 = B-C;
double a2 = Angle(A-C, v2);
v2 = Rotate(v2, -a2/3); // A minus sign indicates clockwise rotation
return GetLineIntersection(B, v1, C, v2);
}
int main(){
int T;
Point A, B, C, D, E, F;
scanf("%d",&T);
while(T--){
A = read_point();
B = read_point();
C = read_point();
D = getD(A, B, C);
E = getD(B, C, A);
F = getD(C, A, B);
printf("%.6lf %.6lf %.6lf %.6lf %.6lf %.6lf\n", D.x, D.y, E.x, E.y, F.x, F.y);
}
return 0;
} That Nice Euler Circuit, Shanghai 2004, LA 3263
Analysis: (still need to think)
If you want to find all areas directly, it will be very troublesome and error prone. However, Euler's theorem can transform the problem and make the solution easier.
Euler theorem : let the number of vertices, edges and faces of the plan graph be V, E and F respectively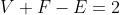
.
In this way, only the number of vertices V and the number of edges E need to be calculated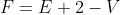
.
The node of the plan consists of two parts: the original node and the new node. Since three lines may be in common, duplicate points need to be deleted. The code is as follows:
/*********************************************************************************
Euler's theorem: let the number of vertices, edges and faces of a plane graph be V, e and f respectively, then V+F-E=2
so...F=E+2-V;
The nodes of the plan are composed of original and new nodes. Since three lines may be in common, duplicate points need to be deleted
*********************************************************************************/
#include<bits/stdc++.h>
using namespace std;
struct Point{
double x,y;
Point(double x=0,double y=0):x(x),y(y){}
};
typedef Point Vector;
//Vector + vector = vector; Vector + point = point
Vector operator + (Vector A,Vector B){return Vector(A.x+B.x,A.y+B.y);}
//Point point = vector
Vector operator - (Point A,Point B){return Vector(A.x-B.x,A.y-B.y);}
//Vector * number = vector
Vector operator * (Vector A,double p){return Vector(A.x*p,A.y*p);}
//Vector / number = vector
Vector operator / (Vector A,double p){return Vector(A.x/p,A.y/p);}
bool operator < (const Point& a,const Point& b){return a.x<b.x||(a.x==b.x && a.y<b.y);}
const double eps = 1e-10;
int dcmp(double x){if(fabs(x)<eps)return 0;else return x < 0 ? -1 : 1;}
bool operator == (const Point& a,const Point& b){return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;}
double Dot(Vector A,Vector B){return A.x*B.x+A.y*B.y;}
double length(Vector A){return sqrt(Dot(A,A));}
double Angle(Vector A,Vector B){return acos(Dot(A,B)/length(A)/length(B));}
double Cross(Vector A,Vector B){return A.x*B.y-B.x*A.y;}
double Area2(Point A,Point B,Point C){return Cross(B-A,C-A);}
/*******Intersection of two straight lines*******/
//Before calling, ensure that the two straight lines P+tv and Q+tv have a unique intersection if and only if Cross(v,w) is not 0;
Point GetLineIntersection(Point P,Vector v,Point Q,Vector w){
Vector u=P-Q;
if(Cross(v,w))
{
double t=Cross(w,u)/Cross(v,w);//When the precision is high, consider customizing the score class
return P+v*t;
}
// else
// return ;
}
/************************
Line segment intersection determination (normal intersection)
************************/
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2){
double c1=Cross(a2-a1,b1-a1);
double c2=Cross(a2-a1,b2-a1);
double c3=Cross(b2-b1,a1-b1);
double c4=Cross(b2-b1,a2-b1);
return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0;
}
/**If intersection at the end point is allowed: if c1 and c2 are both 0, it means collinear; if c1 and c2 are not both 0, it means that an end point is on another line**/
bool OnSegment(Point p,Point a1,Point a2){
return dcmp(Cross(a1-p,a2-p))==0&&dcmp(Dot(a1-p,a2-p))<0;
}
const int mmax=310;
Point P[mmax],V[mmax*mmax];
Point read_point(Point &P){
scanf("%lf%lf",&P.x,&P.y);
return P;
}
int main(){
int n,kase=0;
while(scanf("%d",&n)==1 && n){
for(int i=0;i<n;i++){
P[i]=read_point(P[i]);
V[i]=P[i];
}
n--;
int c=n,e=n;
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++){
if(SegmentProperIntersection(P[i],P[i+1],P[j],P[j+1])){//Strict intersection
V[c++]=GetLineIntersection(P[i],P[i+1]-P[i],P[j],P[j+1]-P[j]);//intersection
}
}
}
// printf("c=%d\n",c);
sort(V,V+c);
c=unique(V,V+c)-V;
// printf("%d=%d-%d\n",c,unique(V,V+c),V);
for(int i=0;i<c;i++){
for(int j=0;j<n;j++){
if(OnSegment(V[i],P[j],P[j+1])) e++;//Number of sides
}
}
printf("Case %d: There are %d pieces.\n",++kase,e+2-c);
}
return 0;
}
/*
5
0 0 0 1 1 1 1 0 0 0
7
1 1 1 5 2 1 2 5 5 1 3 5 1 1
7
1 1 1 5 2 1 2 5 5 1 3 9 1 1
0
*/
analysis:
Let's first look at a simple situation: the route of dog a and dog B is a line segment. Because the motion is relative, it can also be considered that dog a is stationary and dog B walks along a straight line. Therefore, the problem is transformed into finding the minimum or maximum distance from the point to the line segment.
With a simplified version of the analysis, you only need to simulate the whole process. Set the position of the armour dog at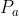
, just numbered
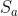Inflection point; B's position is
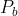, just numbered
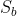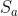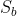Then we only need to calculate which one of the two dogs gets to the inflection point first. The problem before this time point is the "simplified version" we just discussed. After the solution is completed, we need to update the positions of dog a and dog B. if it happens to reach the next inflection point, we need to update itand, and then continue the simulation. Because at least one dog reaches the inflection point every time, the number of times to solve the subproblem does not exceed A+B. The code is as follows:
#include<bits/stdc++.h>
using namespace std;
struct Point{
double x,y;
Point(double x=0, double y=0):x(x),y(y) { }
};
typedef Point Vector;
Vector operator + (Vector A, Vector B) { return Vector(A.x+B.x, A.y+B.y); }
Vector operator - (Point A, Point B) { return Vector(A.x-B.x, A.y-B.y); }
Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }
Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); }
bool operator < (const Point& a, const Point& b) {
return a.x<b.x || ( a.x == b.x && a.y < b.y);
}
const double eps = 1e-10;
int dcmp(double x){
if(fabs(x) < eps) return 0; else return x < 0 ? -1 : 1;
}
bool operator == (const Point& a, const Point& b){
return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0;
}
double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A, A)); }
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }
double Cross(Vector A, Vector B){ return A.x*B.y-A.y*B.x; }
Vector Rotate(Vector A, double rad){
return Vector(A.x*cos(rad)-A.y*sin(rad), A.x*sin(rad)+A.y*cos(rad));
}
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w){
Vector u = P-Q;
double t = Cross(w, u) / Cross(v, w);
return P+v*t;
}
Point read_point(){
Point p;
scanf("%lf %lf",&p.x,&p.y);
return p;
}
double DistanceToSegment(Point P, Point A, Point B){
if(A == B) return Length(P-A);
Vector v1 = B - A, v2 = P - A, v3 = P - B;
if(dcmp(Dot(v1, v2) < 0)) return Length(v2);
else if(dcmp(Dot(v1, v3)) > 0) return Length(v3);
else return fabs(Cross(v1, v2)) / Length(v1);
}
const int maxn = 60;
int T, A, B;
Point P[maxn], Q[maxn];
double Min, Max;
void update(Point P, Point A, Point B){
Min = min(Min, DistanceToSegment(P, A, B));
Max = max(Max, Length(P-A));
Max = max(Max, Length(P-B));
}
int main(){
scanf("%d",&T);
for(int kase = 1; kase <= T; kase++){
scanf("%d%d",&A,&B);
for(int i=0;i<A;i++) P[i]=read_point();
for(int i=0;i<B;i++) Q[i]=read_point();
double LenA=0,LenB=0;
for(int i=0;i<A-1;i++) LenA+=Length(P[i+1]-P[i]);
for(int i=0;i<B-1;i++) LenB+=Length(Q[i+1]-Q[i]);
int Sa=0,Sb=0;
Point Pa=P[0],Pb=Q[0];
Min=1e9,Max=-1e9;
while(Sa<A-1&&Sb<B-1){
double La=Length(P[Sa+1]-Pa); //Distance from a to the next inflection point
double Lb=Length(Q[Sb+1]-Pb); //B distance to the next inflection point
double T=min(La/LenA,Lb/LenB);
//Taking the appropriate unit, the speed of a and B can be LenA and LenB respectively
Vector Va=(P[Sa+1]-Pa)/La*T*LenA; //Displacement vector of a
Vector Vb=(Q[Sb+1]-Pb)/Lb*T*LenB; //Displacement vector of B
update(Pa, Pb, Pb+Vb-Va); //Solve the "simplified version" and update the minimum and maximum distance
Pa=Pa+Va;
Pb=Pb+Vb;
if(Pa==P[Sa+1]) Sa++;
if(Pb==Q[Sb+1]) Sb++;
}
printf("Case %d: %.0lf\n",kase,Max-Min);
}
return 0;
} 2 calculation problems related to circles and spheres
2.1 calculation of circle
Any point on the circle has a unique center angle, so when defining the circle, you can add a function to calculate the coordinates through the center angle. The code is as follows:
struct Point{
double x,y;
Point(double x, double y):x(x), y(y) { }
};
struct Circle {
Point c; //center of a circle
double r; //radius
Circle(Point c, double r):c(c), r(r) { }
Point point(double a){
return Point(c.x + cos(a)*r, c.y + sin(a)*r);
}
};Intersection of line and circle: assume that the line is AB, the center of the circle is C and the radius is r.
① The first method is to solve the equations. Set intersection as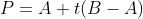
, substituted into the circular equation and sorted out
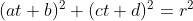After further sorting, the univariate quadratic equation is obtained
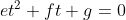. According to the value of the discriminant, it can be divided into three cases: no intersection (separation), one intersection (tangent) and two intersections (intersection). The code is as follows (variables a,b,c,d,e,f,g correspond to the letters in the above equation):
int getLineCircleIntersection(Line L, Circle C, double& t1, double& t2, Vector<Point>& sol){
double a = L.v.x, b = L.p.x-C.c.x, c = L.v.y, d = L.p.y-C.c.y;
double e = a*a+c*c, f = 2*(a*b+c*d), g = b*b+d*d-C.r*C.r;
double delta = f*f-4*e*g; //Discriminant
if(dcmp(delta) < 0) return 0; //disjoint
if(dcmp(delta) == 0){ //Tangent
t1=t2= -f / (2*e); sol.push_back(L.point(t1));
return 1;
}
//intersect
t1 = (-f - sqrt(delta)) / (2*e); sol.push_back(L.point(t1));
t2 = (-f + sqrt(delta)) / (2*e); sol.push_back(L.point(t2));
return 2;
}The function returns the number of intersections, and the parameter sol stores the intersection itself. Note that the above code does not empty the sol, which brings convenience to many problems: you can call this function repeatedly and put all intersections in one sol.
② The second method is geometric method. First find the projection P of the circle center C on AB, and then find the vector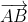Corresponding unit vector
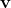, then the two intersections are
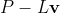and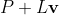
Where L is the distance from P to the intersection (P is equidistant from the two intersections), which can be calculated by Pythagorean theorem. The code is omitted and supplemented.
Intersection of two circles: assume that the center of the circle is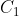
and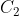
, with radii of
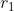and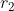
, center distance
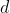, it can be calculated according to the cosine theorem
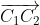reach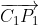
Angle of
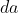, by vector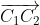Polar angle of
, addition and subtraction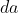You can get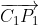and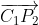
Polar angle of. With the polar angle, it is easy to calculate
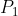and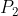
The coordinates of(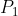and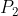Is the intersection of two circles), the code is as follows:
// Calculate vector polar angle
double angle(Vector v){ return atan2(v.y, v.x); }
// Two circles intersect
int getCircleCircleIntersection(Circle C1, Circle C2, vector<Point>& sol){
double d = Length(C1.c - C2.c); //Center distance
if(dcmp(d) == 0){
if(dcmp(C1.r - C2.r) == 0) return -1; //Two circles coincide
return 0; //Two concentric circles
}
if(dcmp(C1.r + C2.r - d) < 0) return 0; //Two circles are separated
if(dcmp(fabs(C1.r-C2.r)-d) > 0) return 0;
double a = angle(C2.c - C1.c); //Polar angle of vector C1C2
double da = acos((C1.r*C1.r + d*d - C2.r*C2.r) / (2*C1.r*d));
//Angle from C1C2 to C1P1
Point p1 = C1.point(a-da), p2 = C1.point(a+da);
sol.push_back(p1);
if(p1 == p2) return 1;
sol.push_back(p2);
return 2;
} Tangent to a circle through a fixed point: find the vector first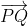
Distance and vector of
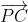The included angle ang, then the vector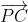The addition and subtraction of the polar angle ang is the polar angle of two tangents. Note that there is no tangent and only one tangent. The code is as follows:
//Tangent from point p to circle C, v[i] is the vector of the ith tangent, and returns the number of tangents
int getTangents(Point p, Circle C, Vector* v){
Vector u = C.c - p;
double dist = Length(u);
if(dist < C.r) return 0;
else if(dcmp(dist-C.r) == 0){ //p on a circle, there is only one tangent
v[0] = Rotate(u, PI/2);
return 1;
}else{
double ang = asin(C.r / dist);
v[0] = Rotate(u, -ang);
v[1] = Rotate(u, +ang);
return 2;
}
} Common tangent of two circles: according to the distance between the centers of two circles, there are six cases in total:
① Case 1: the two circles completely coincide, with countless common tangents.
② Case 2: the two circles contain no common point and no common tangent.
③ Case 3: two circles are inscribed, and there is a common tangent.
④ Case 4: two circles intersect and there are two common tangents.
⑤ Case 5: two circles are circumscribed, with 3 common tangents (1 internal common tangent and 2 external common tangents).
⑥ Case 6: two circles are separated from each other, with 4 common tangents (2 internal common tangents and 2 external common tangents).
These six cases can be identified according to the relationship between center distance and radius, and then solved one by one. Case 1 and case 2 have nothing to solve; The inner common tangent in case 3 and case 5 corresponds to "the tangent of finding a circle through a point on the circle". Just connect the center and tangent point and rotate it by 90 degrees to know the direction vector of the tangent. In this way, the key to the problem is to find the external common tangent in case 4 and 5 and the internal and external common tangent in case 6.
First consider the inner common tangent in case 6, which corresponds to the separation of two circles.
It is not difficult to calculate the angle according to the definition of trigonometric function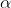, and then calculate through the polar angle as before.
Grandpa tangent is similar. assume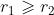
, whether the two circles are separated, tangent or intersecting,
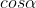All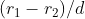
. The rest of the process is the same as before. The code is as follows:
//Returns the number of tangents, - 1 means there are infinite tangents
//a[i] and b[i] are the tangent points of the ith tangent on circle a and circle B respectively
int getTangents(Circle A, Circle B, Point* a, Point* b){
int cnt = 0;
if(A.r < B.r) { swap(A, B); swap(a, b); }
int d2 = (A.x-B.x)*(A.x-B.x) + (A.y-B.y)*(A.y-B.y);
int rdiff = A.r-B.r;
int rsum = A.r+B.r;
if(d2 < rdiff*rdiff) return 0; //Contain
double base = atan2(B.y-A.y, B.x-A.x);
if(d2 == 0 && A.r == B.r) return -1; //Infinite tangents
if(d2 == rdiff*rdiff){ //Inscribed, 1 tangent
a[cnt] = A.getPoint(base); b[cnt] = B.getPoint(base); cnt++;
return 1;
}
//Grandpa tangent
double ang = acos((A.r-B.r) / sqrt(d2));
a[cnt] = A.getPoint(base+ang); b[cnt] = B.getPoint(base+ang); cnt++;
a[cnt] = A.getPoint(base-ang); b[cnt] = B.getPoint(base-ang); cnt++;
if(d2 == rsum*rsum){ //An inner common tangent
a[cnt] = A.getPoint(base); b[cnt] = B.getPoint(PI+base); cnt++;
}else if(d2 > rsum*rsum){ //Two inner common tangents
double ang = acos((A.r+B.r) / sqrt(d2));
a[cnt] = A.getPoint(base+ang); b[cnt] = B.getPoint(PI+base+ang); cnt++;
a[cnt] = A.getPoint(base-ang); b[cnt] = B.getPoint(PI+base-ang); cnt++;
}
return cnt;
} 2.2 sphere related issues
The longitude and latitude are converted into spatial coordinates: the formula is as follows:
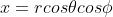
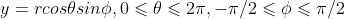
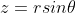
The code is as follows:
//Convert angles to radians
double torad(double deg){
return deg/180 *acos(-1); //acos(-1) is PI
}
//Longitude and latitude (angle) are converted into spatial coordinates
void get_coord(double R, double lat, double lng, double& x, double& y, double& z){
lat = torad(lat);
lng = torad(lng);
x = R*cos(lat)*cos(lng);
y = R*cos(lat)*sin(lng);
z = R*sin(lat);
} Spherical distance: question: given the two points on the spherical surface, how to find their shortest path? Note that you can only walk along the sphere, not through the inside of the sphere. If you walk from the surface, the nearest path is to walk the arc, specifically the great circle arc. Cut the ball with a plane passing through the center of the ball, and the section is a big circle.
How to find the length of the large arc? You don't have to imagine the spatial position of the big circle, but you can imagine them as a plane problem: find the length of the arc with radius r and chord length d. The center angle is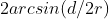
Therefore, the arc length is
.
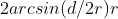2.3 selected examples
1 UVA12304 2D Geometry 110 in 1! Two dimensional geometry 110 in one!
2 UVA1308 Viva Confetti disk problem
3 common algorithms of two-dimensional geometry
| Determination of point in polygon |
| convex hull |
| Half plane intersection |
| Plane area |