Previous The article explains how to parse an input expression into multiple Token s through a regular form, and the core of this article is how to evaluate the expression.
The expressions we enter, that is, the expressions we usually see, are infix expressions - the meaning of infix is that in an expression, the operator is placed in the middle, for example, (1 + 2) * 3, and the operator is in the middle of the number.In the world of computers, however, there are prefix and suffix expressions as well - names make it easy to know that prefix expressions put operators before numbers and suffix expressions put operators after numbers.
| Expression | form |
|---|---|
| Infix | 1 + (3 - 2) * 4 / 5 |
| prefix | + 1 / * - 3 2 4 5 |
| Suffix | 1 3 2 - 4 * 5 / + |
The disadvantage of infix expressions is that once the expression is complex, such as nesting of multiple parentheses, while paying attention to the operator's priority, the code to calculate the value of the infix expression is also very complex.The calculation of prefix and suffix expressions is very simple.
For example, a suffix expression:
- Scan the expression from left to right, and if you encounter a number, put it on the stack
- If you encounter an operator, two numbers N1 and N2 pop up from the stack, which are used to perform operations (n2 op n1) to stack the number of results obtained
- Repeat 1 and 2 until the expression scan ends, and the last remaining number in the stack is the value of the expression.
For example, in the example above, 1 + (3 - 2) * 4/5 = 1.8, for the suffix expression 1 3 2 - 4 * 5 / +:
| Current Token | operation | Stack (top on left) |
|---|---|---|
| 1 | Number of encounters directly stacked | 1 |
| 2 | Number of encounters directly stacked | 3 1 |
| 3 | Number of encounters directly stacked | 2 3 1 |
| - | n1 = 2, n2 = 3; n2 op n1 = 3-2 = 1, and stack 1 | 1 1 |
| 4 | Number of encounters directly stacked | 4 1 1 |
| * | n1 = 4, n2 = 1; n2 op n1 = 4 * 1 = 4, and stack 4 | 4 1 |
| 5 | Number of encounters directly stacked | 5 4 1 |
| / | n1 = 5, n2 = 4; N2 OP N1 = 4/5 = 0.8, and stack 0.8 | 0.8 1 |
| + | n1 = 0.8, n2 = 1; n2 op n1 = 1 + 0.8 = 1.8 and stack 1.8 | 1.8 |
Therefore, it can be seen that calculating a suffix expression is very easy to code.
As you can see from the previous article, what our current Expression class represents is a suffix expression, so we need to provide an algorithm to convert a suffix expression into a prefix or suffix expression so that we can easily calculate the value of the expression.Of course, the flow of the algorithm, our computer ancestors have long thought of, and we just need to make the implementation.
As an example of a suffix expression, the algorithm for converting a suffix expression to a suffix expression follows:
- Initialization operator stack S and list L to hold intermediate results
-
Scan the infix expression from left to right:
- When a number is encountered, add it directly to L
-
When Operator op is encountered
2.1 If S is empty, place op directly on stack S 2.2 If S is not empty and the top of S stack is left parenthesis'('), then op is placed in S stack 2.3 If S is not empty, then the top of the S stack is the operator. If op has a higher priority than the top element of the S stack, then the operator is placed on the S stack 2.4 Otherwise (that is, op has a lower priority than the top element of the S stack), pop up the top element of S and add it to L; then go to 2.1 to continue judging and comparing. -
When encountering brackets
3.1 If left bracket'('), place it directly in stack S 3.2 If it's a right parenthesis')', pop up the operators in S one by one until you encounter a left parenthesis, then discard both parentheses
- Pop up the remaining operators in S and add L
- In this case, all Token s in L are suffix expressions in order
(For more detailed content and examples of infix, prefix, suffix expression conversion algorithms, you can refer to Prefix, infix, suffix expression This article is also a reference for the algorithm flow described in this article.)
Based on the above algorithm, it is not difficult to write an algorithm for converting a suffix Expression to a suffix Expression on the basis of the current Expression. We named this method toPostfixExpr():
/** * Gets the suffix form of the expression * * @return Postfix Expression */ public Expression toPostfixExpr() { ArrayDeque<Token> S = new ArrayDeque<>(); // Operator Stack ArrayList<Token> L = new ArrayList<>(); // Save a list of intermediate results for (Token token : tokens) { switch (token.getType()) { case NUMBER: L.add(token); break; case OPERATOR: Operator op = (Operator) token; boolean back = true; while (back) { back = false; if (S.isEmpty()) { // Operator stack is empty S.push(op); } else { // Operator stack is not empty Token top = S.peek(); // Operator stack top is'(' if (top.isBracket() && ((Bracket) top).isLeft()) { S.push(op); // op takes precedence over the top element of the operator stack } else if (op.isHigherThan((Operator) top)) { S.push(token); } else { // op has less priority than the top element of the operator stack L.add(S.pop()); back = true; // Back to while } } } break; case BRACKET: if (((Bracket) token).isLeft()) { S.push(token); } else { for (Token t = S.pop(); !t.isBracket(); t = S.pop()) { L.add(t); } } break; } } while (!S.isEmpty()) { L.add(S.pop()); } return new Expression(L, true); // true means the expression is a suffix expression }
At this point, we add a boolean field postfix to Expression to identify whether the expression is a suffix expression, which defaults to false, and true to indicate that the expression is a suffix expression.
public class Expression { ... private final List<Token> tokens; // All Token s in this expression private final boolean postfix; // Identification of whether the expression is a suffix expression public Expression(List<Token> tokens, boolean postfix) { this.tokens = tokens; this.postfix = postfix; } /** * Is the expression a suffix expression * * @return Returns true if the expression is a suffix expression, false otherwise */ public boolean isPostfix() { return postfix; } ... }
Then, depending on the suffix expression, it is easy to write a method for calculating the value of the expression, which we call calculate():
/** * Calculate the value of an expression through a suffix expression * * @return The value of the expression */ public Num calculate() { if (!isPostfix()) { throw new RuntimeException("Please convert expression to suffix expression before calculating"); } ArrayDeque<Token> stack = new ArrayDeque<>(); for (Token token : tokens) { if (token.isNumber()) { stack.push(token); } else { Num n1 = (Num) stack.pop(); Num n2 = (Num) stack.pop(); Operator op = (Operator) token; Num result = n2.operate(op, n1); stack.push(result); } } if (stack.size() != 1) { // More than one last number left on the stack indicates a problem with the expression throw new RuntimeException("Wrong expression"); } return (Num) stack.pop(); }
Here we define a operated method in the Num class to operate on two numbers based on an operator:
public static final RoundingMode MODE = RoundingMode.HALF_UP; // Rounding the end decimal by default public static final MathContext MATH_CONTEXT = new MathContext(6, MODE); // Keep 6 significant digits in an infinite loop, rounded to the end public Num operate(Operator op, Num other) { BigDecimal result = null; switch (op.value()) { case '+': result = value.add(other.value); break; case '-': result = value.subtract(other.value); break; case '*': result = value.multiply(other.value); break; case '/': result = value.divide(other.value, MATH_CONTEXT); break; } if (result == null) { throw new RuntimeException(String.format( "operate Method error:%s %s %s", value, op.text(), other.value)); } return new Num(result); }
Everything looks perfect for now - but we've ignored the case where negative numbers are entered.There are two situations at this time:
- The input expression starts with a negative number, such as -1 + 2 * 3, which is easy to solve. We only need to add a 0 at the beginning to adapt to the current program. For example, the expression becomes 0 - 1 + 2 * 3 after adding 0, and the results are consistent
- Another situation is that negative numbers appear in the expression - at this point we need to make special identification of negative numbers, such as using parentheses () to surround negative numbers as usual.So we need to supplement our regular expression so that it can match tokens like (-12) and (-100.100).
Modified Expression (\(-(\d*\\d+|\d+)\)) matches negative numbers):
public class Expression { private static final String REG_EXPR = "\\s*((\\(-(\\d*\\.\\d+|\\d+)\\))|(\\d*\\.\\d+|\\d+)|(\\+|-|\\*|/)|(\\(|\\))|([A-Za-z]+\\(.*\\)))\\s*"; private static final Pattern PATTERN = Pattern.compile(REG_EXPR); ... private static Token getToken(Matcher matcher) { // matcher.group(0) matches the entire regular, matcher.group(1) matches the first parenthesis String m = matcher.group(1); if (m != null) { if (matcher.group(2) != null) { // negative // matcher.group(3) extracts 1.2 from form (-1.2) return new Num("-" + matcher.group(3)); } else if (matcher.group(4) != null) { // Positive number return new Num(matcher.group(4)); } else if (matcher.group(5) != null) { // operator return new Operator(matcher.group(5).charAt(0)); } else if (matcher.group(6) != null) { // brackets return new Bracket(matcher.group(6).charAt(0)); } else if (matcher.group(7) != null) { // function Function function = new Function(matcher.group(7)); Num num = function.getResult(); // Calculate the value of the function directly as a Token return num; } } throw new RuntimeException("getToken"); // It does not happen when there is no error } ... }
Now let's write a main class, get the input from the command line, and calculate the value of the input expression.We'll name the main class Launcher:
public class Launcher { public static void main(String[] args) throws Exception { System.out.println("Welcome to your calculator (input) e(xit) Exit)"); try (Reader in = new InputStreamReader(System.in); BufferedReader reader = new BufferedReader(in)) { String line; while (true) { System.out.print("> "); line = reader.readLine(); if (null == line || "e".equalsIgnoreCase(line) || "exit".equalsIgnoreCase(line)) { break; } else if (line.isEmpty()) { continue; } try { Expression expr = Expression.of(line); Expression postfixExpr = expr.toPostfixExpr(); Num result = postfixExpr.calculate(); System.out.println(result); } catch (ArithmeticException ex) { System.out.println("Operational error:" + ex.getMessage()); } catch (RuntimeException ex) { System.out.println("Run error:" + ex.getMessage()); // ex.printStackTrace(System.err); } } } } }
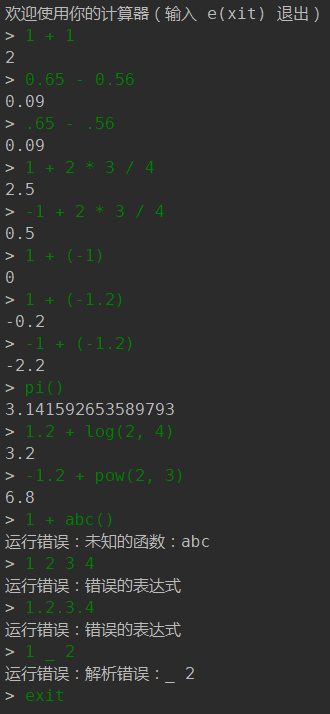
As you can see, we have been able to parse the expression successfully and calculate the value of the expression (the complete source code is in GitHub).
Of course, we can't always run a project with Maven every time we run it, so we package the project as a jar, write a script to execute the jar, and finally add the script to the PATH, then we can call it directly from the command line.
We named the packaged jar mcalc.jar (the packaged configuration can refer to pom.xml) and wrote a simple script.For example, on Windows, write an mcalc.bat:
@echo off :: %~dp0 Indicates the path to the directory where the current batch file is located set DIR_PATH=%~dp0 java -jar %DIR_PATH%mcalc.jar
Then put mcalc.bat and mcalc.jar under the same folder, and add the path of the folder to the PATH.By typing mcalc directly into the command line, you can enter the program: