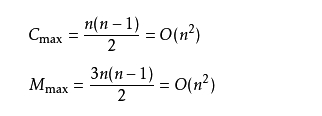catalogue
1.Java multithreading: write two threads to print odd and even numbers from 0 to 100 alternately
3. Implement queue with two stacks
4. Reverse the single linked list
8.Java single linked list for quick sorting
9. Preorder traversal of binary tree
10. Middle order traversal of binary tree
11. Post order traversal of binary tree
12.java implementation of inverse Polish expression
13. Fibonacci sequence and frog jumping steps
1.Java multithreading: write two threads to print odd and even numbers from 0 to 100 alternately
The principle of this implementation is that thread 1 wakes up other threads after printing, then gives up the lock and enters the sleep state. Because when you enter the sleep state, you will not grab the lock with other threads. At this time, only thread 2 is acquiring the lock, so thread 2 is bound to get the lock. Thread 2 executes with the same logic, wakes up thread 1, gives up the lock it holds, and enters the sleep state. This goes back and forth and continues until the task is completed. This achieves the effect of two threads obtaining locks alternately.
private int count = 0;
private final Object lock = new Object();
public void turning() throws InterruptedException {
Thread even = new Thread(() -> {
while (count <= 100) {
synchronized (lock) {
System.out.println("even numbers: " + count++);
lock.notifyAll();
try {
// If not, release the current lock and sleep
if (count <= 100) {
lock.wait();
}
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
});
Thread odd = new Thread(() -> {
while (count <= 100) {
synchronized (lock) {
System.out.println("Odd number: " + count++);
lock.notifyAll();
try {
// If not, release the current lock and sleep
if (count <= 100) {
lock.wait();
}
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
});
even.start();
// Ensure that even threads acquire locks first
Thread.sleep(1);
odd.start();
}
2. Thread safe singleton mode
Double lock judgment mechanism to create singleton mode
public class DoubleCheckLockSinglenon {
private static volatile DoubleCheckLockSinglenon doubleCheckLockSingleon = null;
public DoubleCheckLockSinglenon(){}
public static DoubleCheckLockSinglenon getInstance(){
if (null == doubleCheckLockSingleon) {
synchronized(DoubleCheckLockSinglenon.class){
if(null == doubleCheckLockSingleon){
doubleCheckLockSingleon = new DoubleCheckLockSinglenon();
}
}
}
return doubleCheckLockSingleon;
}
public static void main(String[] args) {
System.out.println(DoubleCheckLockSinglenon.getInstance());
}
}3. Implement queue with two stacks
Title Description
Two stacks are used to implement a queue to complete the Push and Pop operations of the queue. The element in the queue is of type int.
Problem solving ideas
Two stacks, stack1 and stack2.
At the beginning, add the tail element to stack1 each time.
If you need to pop up the queue head element, pop up the element in stack1 and push it into stack2, and then pop up the top element of stack2, that is, the queue head element is popped.
If stack2 is not empty, when adding elements to the end of the queue, they will still be added to stack1, and the team head element will pop up from stack2.
Only when stack2 is empty, the pop-up queue header element needs to transfer the elements in stack1 to stack2.
import java.util.Stack;
public class Solution {
Stack<Integer> stack1 = new Stack<Integer>();
Stack<Integer> stack2 = new Stack<Integer>();
public void push(int node) {
stack1.push(node);
}
public int pop() {
if(stack2.size() == 0) {
while(!stack1.isEmpty()) {
int temp = stack1.peek();
stack2.push(temp);
stack1.pop();
}
}
int res = stack2.peek();
stack2.pop();
return res;
}
}
4. Reverse the single linked list
Single linked list is a common data structure, which is composed of nodes connected by pointers. Each node is composed of two parts: one is the data field, which is used to store node data. The second is the pointer field, which is used to store the address of the next node. Defined in Java as follows:
public class Node {
private Object data;//Data domain
private Node next;//Pointer field
public Node(Object data){
this.data = data;
}
public Node(Object data,Node next){
this.data = data;
this.next = next;
}
public Object getData() {
return data;
}
public void setData(Object data) {
this.data = data;
}
public Node getNext() {
return next;
}
public void setNext(Node next) {
this.next = next;
}
}Let's start with the following idea: the so-called single linked list inversion is to change the pointer field of each node from the original point to the next node to the previous node. However, since the single linked list does not point to the pointer field of the previous node, we need to add a pointer pre to the previous node to store the previous node of each node. In addition, you need to define a pointer cur to save the current node and the next node. After defining the three pointers, traverse the single linked list, point the pointer field of the current node to the previous node, and then move the three pointers back until the traversal stops at the last node.
public static Node reverseListNode(Node head){
//If the single linked list is empty or has only one node, the original single linked list will be returned directly
if (head == null || head.getNext() == null){
return head;
}
//Previous node pointer
Node preNode = null;
//Current node pointer
Node curNode = head;
//Next node pointer
Node nextNode = null;
while (curNode != null){
nextNode = curNode.getNext();//nextNode points to the next node
curNode.setNext(preNode);//Point the next field of the current node to the previous node
preNode = curNode;//The preNode pointer moves backward
curNode = nextNode;//curNode pointer moves backward
}
return preNode;
}5.Binary search in Java
Binary search, also known as half search, has a good search efficiency
Applicable scenario: the sequential storage structure is arranged in order, which is also its disadvantage.
/*
*Recursive binary algorithm
*/
public static int binSearch_2(int key,int[] array,int low,int high){
//Border crossing prevention
if (key < array[low] || key > array[high] || low > high) {
return -1;
}
int middle = (low+high)/2;
if(array[middle]>key){
//Greater than keyword
return binSearch_2(key,array,low,middle-1);
}else if(array[middle]<key){
//Less than keyword
return binSearch_2(key,array,middle+1,high);
}else{
return array[middle];
}
}6. Bubble sorting
N numbers need to be sorted. A total of N-1 times are sorted. The sorting times of each I time is (N-i). Therefore, double loop statements can be used. The outer layer controls the number of cycles, and the inner layer controls the number of cycles per trip, that is
/*
* Bubble sorting
*/
public class BubbleSort {
public static void main(String[] args) {
int[] arr={6,3,8,2,9,1};
System.out.println("The array before sorting is:");
for(int num:arr){
System.out.print(num+" ");
}
for(int i=0;i<arr.length-1;i++){//Outer loop control sorting times
for(int j=0;j<arr.length-1-i;j++){//The inner loop controls how many times to sort each trip
if(arr[j]>arr[j+1]){
int temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
System.out.println();
System.out.println("The sorted array is:");
for(int num:arr){
System.out.print(num+" ");
}
}
}In terms of time complexity:
1. If our data is in positive order, we only need to go once to complete the sorting. The required comparison times C and recording movement times M reach the minimum value, that is, Cmin=n-1;Mmin=0; Therefore, the best time complexity of bubble sorting is O(n).
2. If unfortunately our data is in reverse order, we need to sort n-1 times. n-i comparisons (1 ≤ I ≤ n-1) shall be made for each sequence, and each comparison must move the record three times to reach the exchange record position. In this case, the number of comparisons and moves reaches the maximum:
The worst time complexity of bubble sorting is O(n2).
To sum up, the total average time complexity of bubble sorting is O(n2).
7. Quick sort
Basic idea of quick sort:
1). First, take a number from the sequence as the reference number. 2). In the partition process, all numbers larger than this number are placed on its right, and all numbers less than or equal to it are placed on its left. 3). Repeat the second step for the left and right intervals until there is only one number in each interval.
public class QuickSort {
public static void main(String[] args) {
int [] a = {1,6,8,7,3,5,16,4,8,36,13,44};
QKSourt(a,0,a.length-1);
for (int i:a) {
System.out.print(i + " ");
}
}
private static void QKSourt(int[] a, int start, int end) {
if (a.length < 0){
return ;
}
if (start >= end){
return ;
}
int left = start;
int right = end;
int temp = a[left];
while (left < right){
while (left < right && a[right] >= temp){
right -- ;
}
a[left] = a[right];
while (left < right && a[left] <= temp){
left ++ ;
}
a[right] = a[left];
}
a[left] = temp;
System.out.println(Arrays.toString(a));
QKSourt(a, start, left -1);
QKSourt(a,left+1,end);
}
}8.Java single linked list for quick sorting
The implementation of single linked list is as follows:
(1) Make the first node the center point
(2) Create 2 pointers (p, q). p points to the head node and Q points to the next node of p
(3) q starts to traverse. If it is found that the value of q is smaller than the value of the center point, p = p - > next, and the current value of p and the value of q are exchanged. q can traverse to the end of the linked list
(4) Exchange the value of the head node with the value of p. at this time, p node is the center point and completes one round of fast scheduling
(5) Sorting can be done using recursive methods
public static void main(String[] args) {
ListNode head = new ListNode(2);
ListNode l1 = new ListNode(2);
ListNode l2 = new ListNode(5);
ListNode l3 = new ListNode(3);
ListNode l4 = new ListNode(8);
ListNode l5 = new ListNode(4);
ListNode l6 = new ListNode(2);
ListNode l7 = new ListNode(1);
/*ListNode p = l1;
System.out.println(p.equals(head));
System.out.println(p == head);*/
head.next = l1;
l1.next = l2;
l2.next = l3;
l3.next = l4;
l4.next = l5;
l5.next = l6;
l6.next = l7;
l7.next = null;
ListNode p = head;
while (p.next != null) {
System.out.print(p.val);
p = p.next;
}
System.out.print(p.val);
System.out.println();
ListNode begin = head, end = p;
new SingleLinkedListSorting().quickSort(begin, end);
p = head;
while (p != null) {
System.out.print(p.val);
p = p.next;
}
}
public void quickSort(ListNode begin, ListNode end) {
//If it is empty, judge whether there is only one node
if (begin == null || end == null || begin == end)
return;
//From the first node and a few points after the first node
ListNode first = begin;
ListNode second = begin.next;
int nMidValue = begin.val;
//End condition. second is the last
while (second != end.next && second != null) {
if (second.val < nMidValue) {
first = first.next;
//Make a judgment and avoid the situation that the latter number is smaller than the first number and does not need to be changed
if (first != second) {
int temp = first.val;
first.val = second.val;
second.val = temp;
}
}
second = second.next;
}
//Judge that there are some situations that do not need to be changed to improve the performance
if (begin != first) {
int temp = begin.val;
begin.val = first.val;
first.val = temp;
}
//First part recursion
quickSort(begin, first);
//Posterior fractional recursion
quickSort(first.next, end);
}9. Preorder traversal of binary tree
Preorder traversal (DLR, lchild,data,rchild) is a kind of binary tree traversal, which is also called root first traversal, preorder traversal and preorder traversal. It can be recorded as about the root. Preorder traversal first accesses the root node, then traverses the left subtree, and finally traverses the right subtree.
package test;
//Recursive and non recursive implementation of preorder traversal
import java.util.Stack;
public class Test
{
public static void main(String[] args)
{
TreeNode[] node = new TreeNode[10];//Generate a complete binary tree in the form of an array
for(int i = 0; i < 10; i++)
{
node[i] = new TreeNode(i);
}
for(int i = 0; i < 10; i++)
{
if(i*2+1 < 10)
node[i].left = node[i*2+1];
if(i*2+2 < 10)
node[i].right = node[i*2+2];
}
preOrderRe(node[0]);
}
public static void preOrderRe(TreeNode biTree)
{//Recursive implementation
System.out.println(biTree.value);
TreeNode leftTree = biTree.left;
if(leftTree != null)
{
preOrderRe(leftTree);
}
TreeNode rightTree = biTree.right;
if(rightTree != null)
{
preOrderRe(rightTree);
}
}
public static void preOrder(TreeNode biTree)
{//Non recursive implementation
Stack<TreeNode> stack = new Stack<TreeNode>();
while(biTree != null || !stack.isEmpty())
{
while(biTree != null)
{
System.out.println(biTree.value);
stack.push(biTree);
biTree = biTree.left;
}
if(!stack.isEmpty())
{
biTree = stack.pop();
biTree = biTree.right;
}
}
}
}
class TreeNode//Node structure
{
int value;
TreeNode left;
TreeNode right;
TreeNode(int value)
{
this.value = value;
}
}
10. Middle order traversal of binary tree
Middle order traversal (LDR) is Binary tree traversal One of them, also known as Middle root traversal Travel around in the middle order. In a binary tree, first left, then root, and then right. Qiao Ji: left root right.
import java.util.Stack;
public class Test
{
public static void main(String[] args)
{
TreeNode[] node = new TreeNode[10];//Generate a complete binary tree in the form of an array
for(int i = 0; i < 10; i++)
{
node[i] = new TreeNode(i);
}
for(int i = 0; i < 10; i++)
{
if(i*2+1 < 10)
node[i].left = node[i*2+1];
if(i*2+2 < 10)
node[i].right = node[i*2+2];
}
midOrderRe(node[0]);
System.out.println();
midOrder(node[0]);
}
public static void midOrderRe(TreeNode biTree)
{//Recursive implementation of middle order traversal
if(biTree == null)
return;
else
{
midOrderRe(biTree.left);
System.out.println(biTree.value);
midOrderRe(biTree.right);
}
}
public static void midOrder(TreeNode biTree)
{//Recursive implementation of middle order traversal cost
Stack<TreeNode> stack = new Stack<TreeNode>();
while(biTree != null || !stack.isEmpty())
{
while(biTree != null)
{
stack.push(biTree);
biTree = biTree.left;
}
if(!stack.isEmpty())
{
biTree = stack.pop();
System.out.println(biTree.value);
biTree = biTree.right;
}
}
}
}
class TreeNode//Node structure
{
int value;
TreeNode left;
TreeNode right;
TreeNode(int value)
{
this.value = value;
}
}
11. Post order traversal of binary tree
Postorder traversal (LRD) is Binary tree traversal One of them, also known as Post root traversal After the tour, you can record the left and right roots. Postorder traversal recursive algorithm And non recursive algorithms. In a binary tree, first left, then right, and then root. Qiao Ji: left and right.
import java.util.Stack;
public class Test
{
public static void main(String[] args)
{
TreeNode[] node = new TreeNode[10];//Generate a complete binary tree in the form of an array
for(int i = 0; i < 10; i++)
{
node[i] = new TreeNode(i);
}
for(int i = 0; i < 10; i++)
{
if(i*2+1 < 10)
node[i].left = node[i*2+1];
if(i*2+2 < 10)
node[i].right = node[i*2+2];
}
postOrderRe(node[0]);
System.out.println("***");
postOrder(node[0]);
}
public static void postOrderRe(TreeNode biTree)
{//Recursive implementation of post order traversal
if(biTree == null)
return;
else
{
postOrderRe(biTree.left);
postOrderRe(biTree.right);
System.out.println(biTree.value);
}
}
public static void postOrder(TreeNode biTree)
{//Non recursive implementation of postorder traversal
int left = 1;//Represents the left node in the auxiliary stack
int right = 2;//Represents the right node in the auxiliary stack
Stack<TreeNode> stack = new Stack<TreeNode>();
Stack<Integer> stack2 = new Stack<Integer>();//The auxiliary stack is used to determine whether the child node is in the left node or the right node when returning to the parent node.
while(biTree != null || !stack.empty())
{
while(biTree != null)
{//Push the node into stack 1 and mark the node as the left node in stack 2
stack.push(biTree);
stack2.push(left);
biTree = biTree.left;
}
while(!stack.empty() && stack2.peek() == right)
{//If the parent node is returned from the right child node, the task is completed and the top of the two stacks will pop up
stack2.pop();
System.out.println(stack.pop().value);
}
if(!stack.empty() && stack2.peek() == left)
{//If the parent node is returned from the left child node, the flag is changed to the right child node
stack2.pop();
stack2.push(right);
biTree = stack.peek().right;
}
}
}
}
class TreeNode//Node structure
{
int value;
TreeNode left;
TreeNode right;
TreeNode(int value)
{
this.value = value;
}
}
12.java implementation of inverse Polish expression
The inverse Polish expression writes the operand in front and the operator in the back.
private static List<String> sign=new ArrayList<>();
static {
sign.add("+");
sign.add("-");
sign.add("*");
sign.add("/");
}
public static void main(String[] args) {
String[] arrs={"2", "1", "+", "3", "*"};
System.out.println(evalRPN(arrs)); //9
String[] arrs1={"4", "13", "5", "/", "+"};
System.out.println(evalRPN(arrs1)); //6
}
public static int evalRPN(String[] tokens) {
Stack<Integer> mathStack=new Stack<>();
for (int i = 0; i <tokens.length ; i++) {
String s=tokens[i];
if(sign.contains(s)){
Integer sum=0;
Integer num2=mathStack.pop();
Integer num1=mathStack.pop();
if("+".equals(s)){
sum=num1+num2;
}else if("-".equals(s)){
sum=num1-num2;
}else if("*".equals(s)){
sum=num1*num2;
}else if("/".equals(s)){
sum=num1/num2;
}
// System.out.println(num1+s+num2+"="+sum);
mathStack.push(sum);
}else {
mathStack.push(Integer.parseInt(s));
}
}
return mathStack.pop();
}
13. Fibonacci sequence and frog jumping steps
Recursive method:
public int Fibonacci1(int n) {
if (n <= 0) return 0;
if (n == 1) return 1;
return Fibonacci1(n-1) + Fibonacci1(n - 2);
}Non recursive:
public int Fibonacci2(int n) {
if (n <= 0) return 0;
if (n == 1) return 1;
int i=0;int j=1;
int res=0;
for(int x=2;x<=n;x++){
res = i+j;
i=j;
j=res;
}
return res;
}