👨‍🎓 Blogger homepage: Java tribute dust collection Miraitow
📆 Creation time: 🌴 February 7, 2022 20:23-2:03 🌴
📒 Content introduction: source code analysis of common collections. Later, there may be collections such as ArrayList
📚 Reference: [Xiao Liu speaks source code]
⏳ In short, I encourage you to watch the officials and try new tea with new fire, poetry and wine to take advantage of the time
📝 There are many contents and questions. I hope you can give me some advice 🙏
🎃 Welcome to like 👍 Collection ⭐ Leaving a message. 📝

1. What is Hash

Hash: English is hash, also known as hash
The basic principle is to convert any length input into fixed length output
The rule of this mapping is the Hash algorithm, and the binary string of the original data mapping is the Hash value

2. Features of Hash

• 1. The original data cannot be deduced reversely from the Hash value
• 2. A small change in the input data will result in completely different Hash values, and the same data must result in the same value
• 3. The execution efficiency of Hash algorithm should be efficient, and the Hash value can be calculated quickly for long text
• 4. The collision probability of hash algorithm is small

Because the Hash principle is to map the input space into a Hash space, and the Hash space is far smaller than the input space, according to the drawer principle, there must be different outputs with the same mapping

Drawer principle

There are 10 apples on the table. Put them in 9 drawers. There must be at least 2 apples in one drawer

Another example

There are 50 students, but only 20 nicknames. Each student must have a nickname, so there must be a duplicate nickname (the nickname is equivalent to the bucket of hash, and the student's nickname name is equivalent to the hash value)

3. Explanation of HashMap principle

Inheritance system of HashMap

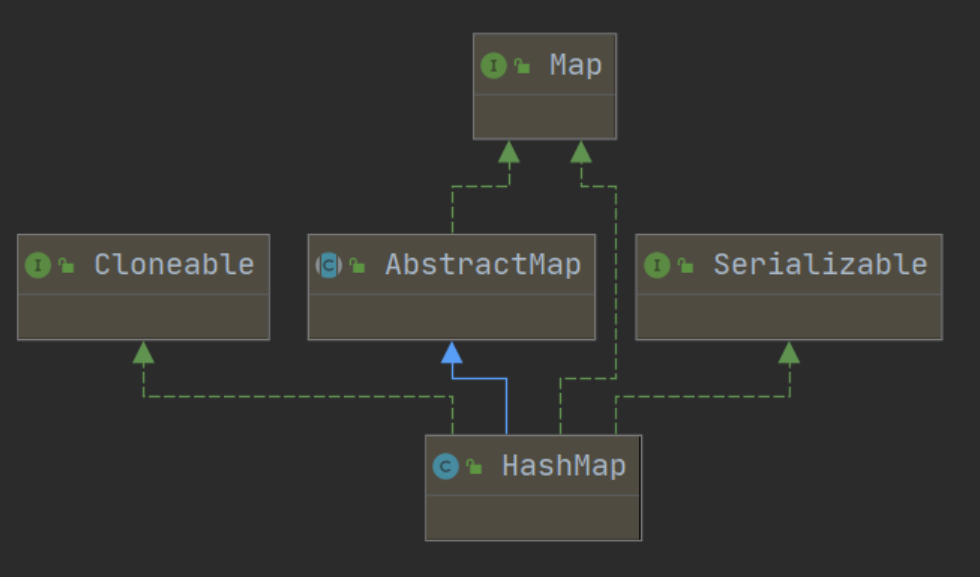
HashMap inherits AbstractMap and implements Cloneable interface, Serializable interface and map < K, V > interface

Data structure analysis of Node

final int hash;
final K key;
V value;
Node<K,V> next;

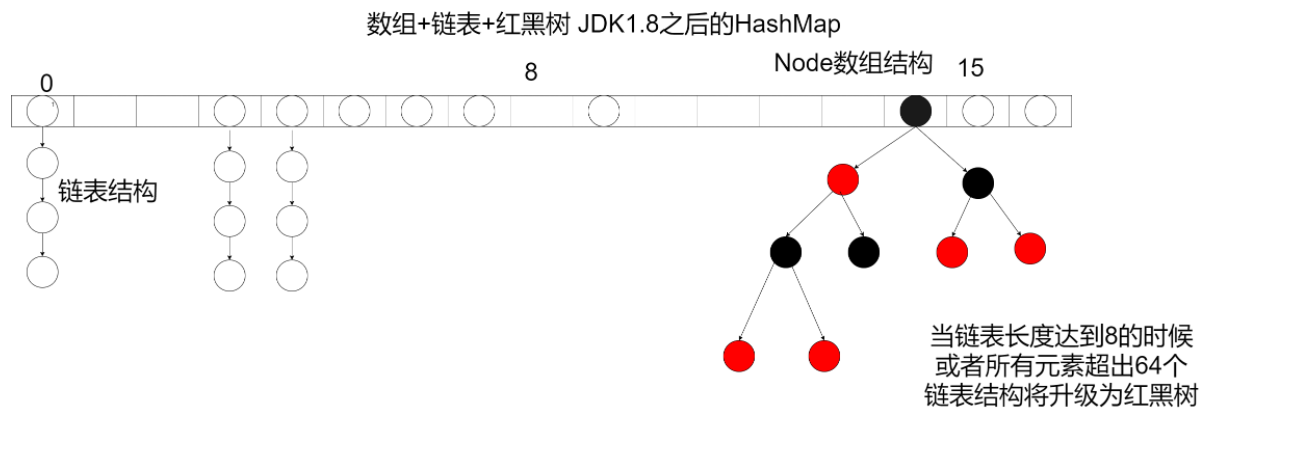
Underlying data structure

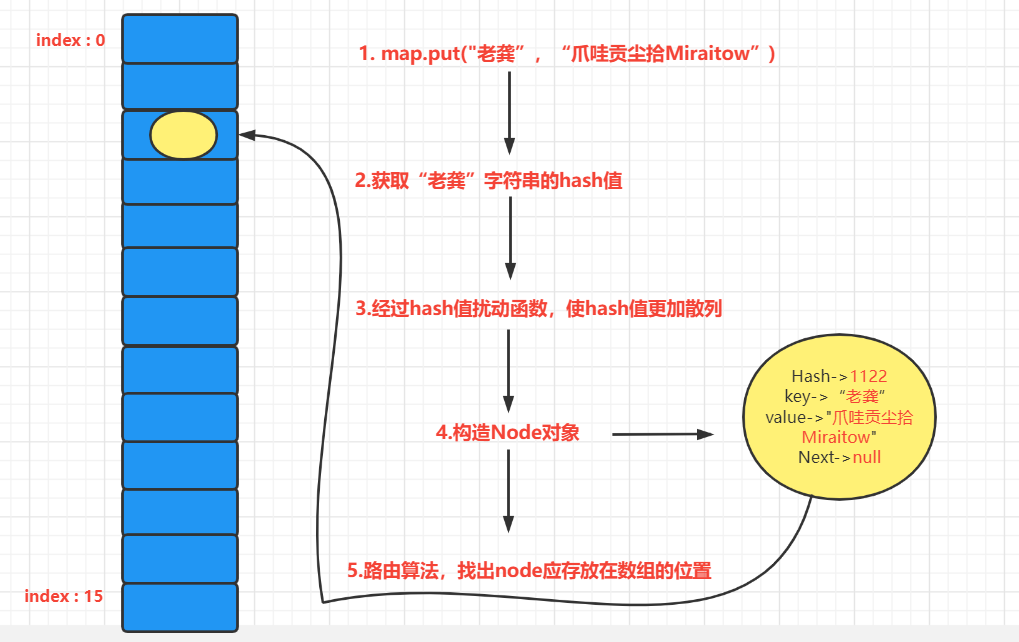
Principle analysis of in put data

What is Hash collision

If I store an element and find that the Hash value of its Key is still 1122, then after the disturbance, its position is still 2. Therefore, there is a conflict at this time, and the conflict should be solved at this time.

Methods to solve Hash collision

• open addressing
• Zipper method [HashMap uses this method]

What is chaining

In jdk1 Before 7, if the amount of data is large, the probability of collision is also large. The collision forms a linked list, which is chaining. At this time, the chain of the zipper method will be very long, which will reduce the search speed (seven up and eight down, the head insertion method before 1.8 and the tail insertion method after 1.8)

So in jdk1 After 8, red and black trees were introduced

Capacity expansion principle of HashMap

Because when there are many data tables, the collision makes the conflict and search speed increase. At this time, it is necessary to expand the capacity

4. Tear source code

HashMap core attribute analysis (threshold, loadFactor, size, modCount)

Threshold: capacity expansion threshold

loadFactor: load factor

size: map actual number of elements

modCount: the number of times a map modifies an element, such as deleting and adding, but modifying the value of the same location does not increase

Constant analysis

The table size is missing. The default initialization capacity is 16

  static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

Maximum length of table

static final int MAXIMUM_CAPACITY = 1 << 30;

The default load factor is 0.75. It is not recommended to set it yourself, which is calculated by scientists

static final float DEFAULT_LOAD_FACTOR = 0.75f;

Tree threshold

static final int TREEIFY_THRESHOLD = 8;

Tree demotion to linked list threshold

static final int UNTREEIFY_THRESHOLD = 6;

Not when the linked list reaches 8, it can be trealized, but when the element reaches 64 and the chain is expressed to 8

static final int MIN_TREEIFY_CAPACITY = 64;

Attribute analysis

Hashtable

  transient Node<K,V>[] table;

  transient Set<Map.Entry<K,V>> entrySet;

Number of elements in the current hash table

  transient int size;

Modification times of current hash table structure
(you insert an element or subtract an element. Note that replacement is not a table structure modification, and addition and subtraction will not be performed)

  transient int modCount;

Capacity expansion threshold. When the current hash table exceeds the threshold, capacity expansion is triggered
threshold=capacity * loadFactor
The default is 16 * 0.75 = 12, which means that the capacity is expanded when the number of elements is greater than 12

  int threshold;

Load factor, generally not changed (0.75)

  final float loadFactor;

Analysis of construction method

There are four constructors

1. Construction method with two parameters (int initialCapacity, float loadFactor)

public HashMap(int initialCapacity, float loadFactor) {
//Throw an exception object when the initial capacity is less than zero
    if (initialCapacity < 0)
        throw new IllegalArgumentException("Illegal initial capacity: " +
                                           initialCapacity);
    //If the initial capacity is greater than the maximum capacity of the array, set the initial capacity to the maximum capacity
    if (initialCapacity > MAXIMUM_CAPACITY)
        initialCapacity = MAXIMUM_CAPACITY;
        //NaN is actually short for Not a Number
        //The value of 0.0f/0.0f is NaN. From a mathematical point of view, 0 / 0 is uncertain.
    if (loadFactor <= 0 || Float.isNaN(loadFactor))
        throw new IllegalArgumentException("Illegal load factor: " +
                                           loadFactor);
    this.loadFactor = loadFactor;
    //The reason why initialCapacity is not assigned directly is to ensure that the number is to the power of 2
    this.threshold = tableSizeFor(initialCapacity);
}

Let's see how tableSizeFor is implemented

Function: returns the N-th power greater than the minimum 2 of cap. For example, 16 is returned when cap = 10, 32 is returned when cap = 28, and this number must be to the power of 2
cap=10
n=10 -1=9;
0b1001 | 0b0100=>0b1101
0b1101 | 0b0011=>0b1111
0b1111 | 0b0000=>0b1111
0b1111 | 0b0000=>0b1111
0b1111 | 0b0000=>0b1111
Ob1111 = > to decimal is 15
return 16
So why did you lose one at the beginning?
If there is no minus one
hypothesis
cap=16
0b10000 | 0b01000 =>0b11000
0b11000 | 0b00100=>0b11110
0b11110 | 0b00001 =>0b11111
0b11111 | 0b00000=>0b11111
0b11111 | 0b00000=>0b11111
Ob11111 = > Convert to decimal 31
return 32
What we passed in is 16, and the result becomes 32, which is obviously inconsistent with the assumption that a number is 0001 1101 1100 = > 0001 1111 1111 + 1 = > 0010 0000 0000 must be the power of 2

• The purpose of reassigning cap-1 to n is to find another target value that is greater than or equal to the original value. For example, binary 1000, decimal value is 8. If you don't operate directly without subtracting 1 from it, you will get the answer 10000, that is 16. Obviously not the result. After subtracting 1, the binary is 111, and then the operation will get the original value of 1000, that is, 8.

• Maximum in HashMap_ Capability is the 30th power of 2. Combined with the implementation of tableSizeFor(), the reasons for setting are as follows:
  The maximum positive number of int can reach the 31st-1st power of 2, but there is no way to get the 31st power of 2. Therefore, the capacity cannot reach the 31st power of 2. We also need to make the capacity meet the power of 2. So set it to the 30th power of 2

   static final int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }

public HashMap(int initialCapacity) {
    this(initialCapacity, DEFAULT_LOAD_FACTOR);
}

public HashMap() {
    this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}   

public HashMap(Map<? extends K, ? extends V> m) {
    this.loadFactor = DEFAULT_LOAD_FACTOR;
    putMapEntries(m, false);
}

Core knowledge point: why does the length of a table have to be a power of 2

• The algorithm for calculating Hash value is actually taking modulus, hash%length,

• The efficiency of direct redundancy in the computer is not as good as that in the source code of displacement operation. Hash& (length-1)

• To ensure hash% length = = hash & (length-1)

• Then length must be the nth power of 2;

HashMap put method analysis - putVal

public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

// Disturbance function
// Function: how to make 16 bits higher than the hash value of the key participate in routing operation when the table is relatively short
// XOR: 0 for the same, 1 for the different

// h = 0b 0010 0101 1010 1100 0011 1111 0010 1110

// 0b 0010 0101 1010 1100 0011 1111 0010 1110 [h]
// ^
// 0b 0000 0000 0000 0000 0010 0101 1010 1100 [h >>> 16]
// => 0010 0101 1010 1100 0001 1010 1000 0010
// When the table is not very long, let the high 16 bits also participate in order to reduce conflicts and collisions
static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);}

// The core method of put
// Hash: hash value of key
// key: key
// value: value
// onlyIfAbsent: if true, do not change the existing value
// evict: if false, the table is in creation mode.
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    // tab: hash table referencing the current hashMap
    // p: Elements of the current hash table
    // n: Indicates the length of the current hash table
    // i: Indicates the result of route addressing
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    
    // Delay initialization logic. When putVal is called for the first time, it will initialize the hash table that consumes the most memory in the hashMap object
    // If the table is null or the length is 0, the creation starts
    if ((tab = table) == null || (n = tab.length) == 0)
        // It will not be initialized until the data is inserted for the first time
        n = (tab = resize()).length;
    
    // In the simplest case, the bucket bit found by addressing is just null. At this time, it is directly assigned to the calculated position
    // tab and n are assigned in the previous if
    // Perform a routing operation (n - 1) & hash] to get the hash address
    // If there is no such element in the tab or it is equal to null
    if ((p = tab[i = (n - 1) & hash]) == null)
        // To create a new Node, k-v encapsulates a Node and places it in the i position of the tab
        tab[i] = newNode(hash, key, value, null);
    
    // At this time, it may be an array, a linked list or a red black tree
    else {
        // e: If it is not null, an element consistent with the k-v to be inserted is found
        // k: Represents a temporary K
        Node<K,V> e; K k;
        // p: Get in another branch if
        // Indicates that the element in the bucket is exactly the same as the key of the element you are currently inserting. Subsequent replacement operations will be performed
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
        // p: It's already treelized
        else if (p instanceof TreeNode)
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        //It's a linked list
        else {
            // The header element of the linked list is inconsistent with the key to be inserted,
            for (int binCount = 0; ; ++binCount) {
                // If you get to the end, add p to the last position
                if ((e = p.next) == null) {
                    p.next = newNode(hash, key, value, null);
                    // If the binCount of the current linked list is greater than the value of the benchmark tree, the tree operation will be performed
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        // Tree operation
                        treeifyBin(tab, hash);
                    break;
                }
                // How to make hash es equal and key s equal requires replacement
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                // loop
                p = e;
            }
        }
        // If e is not null, find the old value and return
        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                // Overwrite new value
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }
    //The number of modifications increases, and the replacement of Node elements does not count
    ++modCount;
    // If the size of the table is larger than the threshold, execute resize() to expand the capacity
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    return null;
}

Core analysis of HashMap resize capacity expansion method

// resize() method
// Why do we need to expand capacity?
// When there are more and more elements, the search speed of hashMap increases from O(1) to O(n), resulting in serious chaining,
// In order to solve the decline of query efficiency caused by conflict, it is necessary to expand [capacity expansion is a very bad action]
final Node<K,V>[] resize() {
    // oldTab: refers to the hash table before capacity expansion
    Node<K,V>[] oldTab = table;
    // oldCap: indicates the length of the table array before capacity expansion
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    // oldThr: indicates the threshold value before capacity expansion and triggers the preview of this capacity expansion
    int oldThr = threshold;
    // newCap: size of table array after capacity expansion
    // newThr: the condition that triggers the next expansion after the expansion
    int newCap, newThr = 0;
    // If the condition is true, it indicates that the hash table in hashMap has been initialized and is a normal expansion
    if (oldCap > 0) {
        // If the length of the current array is greater than the maximum size that the hashMap can accommodate, it will not be expanded, and the original array will be returned directly
        // Set the maximum capacity expansion threshold to the maximum value of int
        if (oldCap >= MAXIMUM_CAPACITY) {
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        // The size of the new table is twice that of the source table
        // Notify that the newCap after capacity expansion is less than the maximum limit of the array, and the threshold before capacity expansion is 16
        // In this case, the threshold of the next expansion is doubled
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            // The capacity expansion threshold is also doubled
            newThr = oldThr << 1; // double threshold
    }
    // oldCap == 0 [description hash table null in hashMap] 
    // 1.new HashMap(initCap,loadFactor)
    // 2.new HashMap(intiCap)
    // 3.new HashMap(map) and the Map has data
    else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr;
    
    // oldCap == 0 && oldThr == 0
    // new HashMap(); When
    else {               // zero initial threshold signifies using defaults
        newCap = DEFAULT_INITIAL_CAPACITY; // 16
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY); //12
    }
    // When the newThr is 0, calculate a newThr through newCap and loadFactor
    if (newThr == 0) {
        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    // The update threshold is the calculated newThr
    threshold = newThr;
    @SuppressWarnings({"rawtypes","unchecked"})
    // Create a large array
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
    // Then update the reference of table
    table = newTab;
    // oldTab is not null, which means that the table of hashMap is not null before this expansion
    if (oldTab != null) {
        // Iterate one location at a time
        for (int j = 0; j < oldCap; ++j) {
            // e: Current node
            Node<K,V> e;
            // Iteration bucket node. If the node is not empty, it needs to be calculated
            // However, the specific formula of the data in the bucket (single data, linked list, tree) is uncertain and needs to be judged
            if ((e = oldTab[j]) != null) {
                // Empty the original array data and wait for GC to recycle. The original data already exists e inside
                oldTab[j] = null;
                // Descriptive single element data,
                if (e.next == null)
                    // Directly calculate the hash value and put it in
                    newTab[e.hash & (newCap - 1)] = e;
                // If it has been trealized
                else if (e instanceof TreeNode)
                    // Explain in the red and black tree section
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                // If it's a linked list
                else { // preserve order
                    // The bucket position has formed a linked list
                    
                    // Low linked list: the subscript position of the array stored after capacity expansion, which is consistent with the subscript position of the current array
                    Node<K,V> loHead = null, loTail = null;
                  	// High order linked list: stored in the subscript position of the array after capacity expansion,
                    // Subscript position of current array + length of array before capacity expansion
                    Node<K,V> hiHead = null, hiTail = null;
                    
                    // An element of the current linked list
                    Node<K,V> next;
                    do {
                        next = e.next;
                        // hash -> .... 1 1111 
                        // hash -> .... 0 1111 
                        // 0b 1 0000
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    // Low linked list has data
                    if (loTail != null) {
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    // High linked list has data
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    // When finished, return to the new
    return newTab;
}

Analysis of HashMap get method

// Get a method
public V get(Object key) {
    Node<K,V> e;
    // First call hash(key) to calculate hash value, then call getNode method.
    return (e = getNode(hash(key), key)) == null ? null : e.value;
}

// getNode method
final Node<K,V> getNode(int hash, Object key) {
    // tab: hash table referencing the current hashMap
    // first: header element in bucket
    // e: Temporary node element
   	// n: table array element
    Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
    // First, judge that the table is not empty and the length is not 0, and the first part is null
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (first = tab[(n - 1) & hash]) != null) {
        // Judge the first first. If the hash values are equal and the key s are equal, return the current node
        if (first.hash == hash && // always check first node
            ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
        // If the next of first is not null
        if ((e = first.next) != null) {
            // If it is a tree, the lookup method of the tree is called
            if (first instanceof TreeNode)
                return ((TreeNode<K,V>)first).getTreeNode(hash, key);
            // If it is a linked list, it will be judged circularly
            do {
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null);
        }
    }
    // If none, null is returned
    return null;
}

Analysis of HashMap remove method

// Method of removing elements
public V remove(Object key) {
    Node<K,V> e;
    // Call the hash method to get the hash value, then call removeNode.
    return (e = removeNode(hash(key), key, null, false, true)) == null ?
        null : e.value;
}

// Core method removeNode
// Hash: hash value
// key: key
// Value: value if matchValue, the matching value will be. Otherwise, it will be ignored
// matchValue: if true, it will be deleted only when the values are equal
// movable: if the false node is deleted, other nodes will not be moved
final Node<K,V> removeNode(int hash, Object key, Object value,
                           boolean matchValue, boolean movable) {
    // tab: hash table referencing the current hashMap
    // p: Current node element
    // n: Indicates the length of the hash table array
    // index: indicates the addressing result
    Node<K,V>[] tab; Node<K,V> p; int n, index;
    
    // Judge whether the table is empty, whether the length is 0, and the corresponding hash value exists in the array before continuing to go down
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (p = tab[index = (n - 1) & hash]) != null) {
        // It indicates that the bucket bit is generated by data and needs to be searched and deleted
        // node: found results
        // e: Next element of the current Node
        Node<K,V> node = null, e; K k; V v;
        // Judge whether the header element is the element to be deleted. If so, put it in node
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            node = p;
        // The first one in the bucket is not
        else if ((e = p.next) != null) {
            // Tree structure
            if (p instanceof TreeNode)
                // Result of call tree
                node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
            else {
                // The linked list structure is obtained by circular traversal
                do {
                    if (e.hash == hash &&
                        ((k = e.key) == key ||
                         (key != null && key.equals(k)))) {
                        node = e;
                        break;
                    }
                    p = e;
                } while ((e = e.next) != null);
            }
        }
        // Judge whether the target node to be deleted is obtained
        if (node != null && (!matchValue || (v = node.value) == value ||
                             (value != null && value.equals(v)))) {
            // If it is a tree node, call the delete operation of the tree
            if (node instanceof TreeNode)
                ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
            // If node = p, it is the first data
            else if (node == p)
                // Update the address to the next data and put it into the bucket
                tab[index] = node.next;
            else
                // If node is not equal to p, it will directly point to the address of the next element in the linked list
                p.next = node.next;
            // Increase in modification times
            ++modCount;
            // Size minus 1
            --size;
            afterNodeRemoval(node);
            // Return deleted node
            return node;
        }
    }
    // If none is executed, null is returned
    return null;
}

Analysis of HashMap replace method

// Replace by k and v
@Override
public V replace(K key, V value) {
    Node<K,V> e;
    if ((e = getNode(hash(key), key)) != null) {
        V oldValue = e.value;
        e.value = value;
        afterNodeAccess(e);
        return oldValue;
    }
    return null;
}

// Replace with k oldValue newValue 
@Override
public boolean replace(K key, V oldValue, V newValue) {
    Node<K,V> e; V v;
    if ((e = getNode(hash(key), key)) != null &&
        ((v = e.value) == oldValue || (v != null && v.equals(oldValue)))) {
        e.value = newValue;
        afterNodeAccess(e);
        return true;
    }
    return false;
}

5. HashMap summary

• The default capacity of HashMap is 16 (1 < < 4). Each time it exceeds the threshold, it will be automatically expanded by twice the size, so the capacity is always 2^N power. In addition, the underlying table array is delayed initialization, which is initialized only after the key value pair is added for the first time.

• The default load factor of HashMap is 0.75. If we know the size of HashMap, we need to set the capacity and load factor correctly.

• When each slot of HashMap meets the following two conditions, it can be transformed into a red black tree to avoid that when the slot is a linked list data structure, the linked list is too long, resulting in too slow search performance.

  1. Condition 1: the table array of HashMap is greater than or equal to 64.
  2. Condition 2: when the length of the slot linked list is greater than or equal to 8. The reason for choosing 8 as the threshold is that the probability (Poisson distribution) is less than one in ten million.

• When the number of nodes of the red black tree in the slot is less than or equal to 6, it will degenerate back to the linked list.

• The average time complexity of finding and adding key value pairs in HashMap is O(1).

• For the node whose slot is a linked list, the average time complexity is O(k). Where k is the length of the linked list.

• For the node whose slot is red black tree, the average time complexity is O(logk). Where k is the number of red black tree nodes.