1. Stack
1.1 definition of stack
Stack is a linear table that is restricted to insert and delete operations only at the end of the table
We call the end that allows insertion and deletion as the top of the stack and the other end naturally as the bottom of the stack;
A stack without data elements is called an empty stack;
The stack is characterized by a Last In First Out linear table, referred to as LIFO structure. The stack itself is a linear table, and its data elements have linear relations, but it is a special linear table.
Stack insertion is called stack entry, also known as stack pressing, stack entry, and stack deletion is called stack exit, also known as pop stack.
1.2 implementing ArrayStack based on ArrayList
1. Create Stack interface
package ifce;
public interface Stack<E> extends Iterable<E> {
public int size();//Returns the number of elements
public boolean isEmpty();//Judgment null
public void push(E element);//Stack pressing
public E pop();//Out of stack
public E peek();//View stack top element
public void clear();//Empty stack
}
2.ArrayStack implementation class
It is relatively simple. It mainly calls the ArrayList method of sequence table 01;
package linestract;
import ifce.Stack;
import java.util.Iterator;
import java.util.Objects;
public class ArrayStack<E> implements Stack<E>{
private ArrayList<E> list;
public ArrayStack(){
list = new ArrayList<>();
}
public ArrayStack(int capacity){
list = new ArrayList<>(capacity);
}
@Override
public int size() {
return list.size();
}
@Override
public boolean isEmpty() {
return list.isEmpty();
}
@Override
public void push(E element) {
list.add(element);
}
@Override
public E pop() {
return list.remove(list.size()-1);
}
@Override
public E peek() {
return list.get(list.size()-1);
}
@Override
public void clear() {
list.clear();
}
@Override
public Iterator<E> iterator() {
return list.iterator();
}
@Override
public boolean equals(Object o) {
if(o == null){
return false;
}
if (this == o) return true;
if(o instanceof ArrayStack){
ArrayStack other = (ArrayStack)o;
return other.list.equals(this.list);
}
return false;
}
@Override
public String toString() {
return list.toString();
}
}
1.3 test class of arraystack
package test;
import linestract.ArrayStack;
import java.util.Iterator;
public class ArrayStackTest {
public static void main(String[] args) {
ArrayStack<Integer> stack01 = new ArrayStack<>();
ArrayStack<Integer> stack02 = new ArrayStack<>(15);
for(int i = 0;i<=11;i++){
stack01.push(i);
stack02.push(i);
}
System.out.println(stack01.toString());
System.out.println(stack02.toString());
System.out.println(stack01.equals(stack02));
System.out.println("========================");
System.out.println(stack01.pop());
System.out.println(stack01.toString());
System.out.println(stack01.peek());
System.out.println("=========================");
Iterator<Integer> it = stack02.iterator();
while(it.hasNext()){
System.out.println(it.next());
}
for(Integer num : stack01){
System.out.println(num);
}
}
}

2. Practice using stacks to solve problems
2.1 infix expression to suffix expression, and complete the calculation
2.2 hex to decimal
For (9FBF1), we take the character from the end and multiply its corresponding value by the power of 16 [0,length()-1]. After understanding this,
*We create a stack, put each character of our string on the stack, and define the sum and power variables. Because the stack is last in first out, the elements out of the stack are exactly the elements we want. As long as the stack is not empty, we
*Perform the operation; Here we use the getNumber() method, which is used to judge whether characters are numbers, 0-9, and A-F; Not in this range, we can throw an exception directly. In the 0-9 range, we let
*Characters - '0', they are ASCII code for operation; For A-F, we do the same, but we need to add 10, because a represents 10 in decimal system. If ch is a, ch-'A 'is 0. We need to add the difference
package jinzhi;
import linestract.ArrayStack;
public class HexToDec {
public static void main(String[] args) {
String hex = "9FBF1";
System.out.println(HexToDec(hex));
}
public static int HexToDec(String str){
ArrayStack<Character> stack = new ArrayStack<>();
for(int i = 0;i<str.length();i++){
stack.push(str.charAt(i));
}
int sum = 0;
int mi = 0;
while(!stack.isEmpty()){
char ch = stack.pop();
sum += getNumber(ch)*Math.pow(16,mi);
mi++;
}
return sum;
}
private static int getNumber(char ch) {
if(!(ch>='A' && ch<='F' || ch >='0' && ch <='9')){
throw new IllegalArgumentException("Parameter exception");
}else if(ch >='0' && ch <='9'){
return ch - '0';
}else{
return ch - 'A' + 10;
}
}
}
2.3 decimal to hexadecimal
Decimal to hexadecimal, we let it take the remainder of 16. If the remainder is in the range of 0-9, it will be converted into A string for stack pressing. If it is in the range of 10-15; The ASCII code corresponding to A is 65; We add A difference of 55 to the remainder, remember to change it to char type, and then splice the empty string, because if we don't turn it, the number and the empty string will be spliced. After the loop, as long as the stack is not empty, we use Stringb to splice and return it; What we want is to splice the remainder from the last one forward, and the stack just helps us solve this problem.
package jinzhi;
import linestract.ArrayStack;
public class DecToHex {
public static void main(String[] args) {
ArrayStack<String> stack = new ArrayStack<>();
int num = 654321;
while(num > 0){
int num1 = num % 16;
if(num1 < 10){
stack.push(num1 + "");
}else{
stack.push((char)(num1+55)+"");
}
num /= 16;
}
StringBuilder stringBuilder = new StringBuilder();
while(!stack.isEmpty()){
stringBuilder.append(stack.pop());
}
System.out.println(stringBuilder.toString());
}
}
2.4 judging palindromes
Let's first say what is palindrome. Palindrome is simply the same as reading from front to back and from back to front. For example, Shanghai's tap water comes from the sea (odd number) and 123321 (even number);
Method 1: we use double pointers; Define two variables to traverse from both sides. If it is not palindrome exit or normal end (when the left variable is greater than or equal to the right variable), it is palindrome;
//Method of using double pointer
public static boolean solution2(String str){
int i = 0;
int j = str.length()-1;
while(true){
if(str.charAt(i)==str.charAt(j)){
i++;
j--;
}else{
return false;
}
if(j<=i){
return true;
}
}
}
Method 2: use the stack, but use the stack to solve the palindrome problem; It has a bug,112233. Finally, the stack is empty and returns true, but it is not a palindrome; Let's just practice using the stack.
Specific implementation: first of all, we need to know that if it is an odd number, we don't need to put the middle one on the stack and let it skip; If it is an even number, it is normal to judge whether the stack is empty, then it will enter the stack. If it is not empty, it will judge whether the top element of the stack is the same as the traversed element. If it is the same, it will exit the stack, and if it is different, it will enter the stack. The left back can judge whether the stack is empty.
package jinzhi;
import linestract.ArrayStack;
public class JudgingPalindrome {
public static void main(String[] args) {
solution01("112233");
boolean f1 = solution2("112233");
boolean f2 = solution2("Shanghai tap water comes from the sea");
System.out.println( f1 + "\t"+f2);
}
//Use stack to solve palindrome problem; There is a bug in using stack, 112233
public static void solution01(String str){
ArrayStack<Character> stack = new ArrayStack<>();
for(int i=0;i<str.length();i++){
//If the length of the string is odd, it doesn't need to be put on the stack. Let's just let it skip.
if(str.length() % 2 == 1 && str.length() / 2 == i){
continue;
}
char ch = str.charAt(i);
if(stack.isEmpty()){
stack.push(ch);
}else{
if(stack.peek() != ch){
stack.push(ch);
}else{
stack.pop();
}
}
}
System.out.println(stack.isEmpty());
}
}
2.5 bracket matching
The so-called bracket matching is the correspondence between brackets. We have four brackets < >, (), [], {}, one-to-one correspondence;
Method 1: use HashMap; Set the left bracket as the Key and the right bracket as the value; First, store the corresponding parentheses in the HashMap set, then create a stack, traverse the string, and get each character element. If the stack is empty, enter the stack. If it is not empty, use the element at the top of the stack as a Key to query whether its value is the same as the currently traversed element. Note that we must first judge whether the Key exists in the HashMap, because the left parenthesis in the map decreases, If a closing bracket is just better when entering, it will not be found, and it will report a null pointer. The reason why the top element of the stack is used as the Key is because the keys are left parentheses. You can get the corresponding right parentheses. If the obtained elements are the same as the traversal elements, it means that they match, so you can get out of the stack. Finally, judge whether the stack is empty;
//We use hashMap
public static void matches02(String str){
HashMap<Character,Character> map = new HashMap<>();
map.put('[',']');
map.put('(',')');
map.put('{','}');
map.put('<','>');
ArrayStack<Character> stack = new ArrayStack<>();
for(int i = 0;i<str.length();i++){
if(stack.isEmpty()){
stack.push(str.charAt(i));
}else{
char top = stack.peek();
//Get the value through the key and compare it with the top of the stack; But one problem is that we must first ensure that the key exists; Null pointer will be reported if it does not exist;
if(map.containsKey(top) && map.get(top)==str.charAt(i)){
stack.pop();
}
}
}
System.out.println(stack.isEmpty());
}
Method 2: by looking at the ASCII code table, you will find that the difference between < >, [], {} is - 1, and the difference between () is - 1 (both left minus right);
Therefore, we only need to traverse the string. If the stack is empty, we will enter the stack. If not, we will judge whether the difference between the top element of the stack minus the traversal element is - 1 or - 2. If yes, we will exit the stack and if not, we will enter the stack; Because of the operation, the stack storage type is Character type.
package jinzhi;
import linestract.ArrayStack;
import java.util.HashMap;
public class MatchBraket {
public static void main(String[] args) {
matches01("<>{(()}[]");
matches02("<>{()}[]");
}
//Using stack to solve bracket matching problem; The ASCII code difference of {}, [], < >, is - 2, and the () difference is - 1;
public static void matches01(String str){
ArrayStack<Character> stack = new ArrayStack<>();
for(int i = 0;i<str.length();i++){
char ch = str.charAt(i);
if(stack.isEmpty()){
stack.push(ch);
}else{
if(stack.peek()-ch == -2 || stack.peek() - ch == -1){
stack.pop();
}else{
stack.push(ch);
}
}
}
System.out.println(stack.isEmpty());
}
}
3. Double ended stack
3.1 what is a dual ended stack
Double ended stack refers to the operation of taking both ends of a linear table as the bottom of the stack to enter and exit the stack respectively. There is only one linear table;
It makes use of the fact that the position of the bottom of the stack is fixed and the position of the top of the stack is constantly changing;
It is also a kind of linear table and a special classification of stack; So we can implement it with the idea of dynamic array and stack.

3.2 implementation of dual end stack
3.2.1 definition of variables and construction methods
Variables include left stack top, right stack top, stored data, stack initialization capacity, etc;
In the nonparametric construction method, you need to create an array of initial capacity; And assign - 1 to the left stack top and length to the right stack top; Because the Java shaping variable has no assignment initialization, it will default to 0;
package linestract;
import java.util.Iterator;
public class ArrayDoubleEndStack<E> implements Iterable<E> {
private int ltop;
private int rtop;
private E[] data;
private static int DEFAULT_CAPACITY = 10;
public ArrayDoubleEndStack(){
data = (E[])new Object[DEFAULT_CAPACITY];
ltop = -1;
rtop = data.length;
}
3.2.2 stacking operation
We have two types of double end stack entry, one is left stack entry, the other is right stack entry;
Since the two stack tops are the first and last outside the array subscript range respectively, before entering the stack, you need to perform + 1 and - 1 operations respectively to assign values; Also, like the implementation of ArrayList, we need to judge whether the stack is full before entering the stack element. If it is full, we need to expand the capacity. We use the resize() method to expand the capacity. This method is implemented below.
public void pushLeft(E element){
if(ltop + 1 ==rtop){
resize(2*data.length);
}
data[++ltop] = element;
}
public void pushRight(E element){
if(ltop + 1 ==rtop){
resize(2*data.length);
}
data[--rtop] = element;
}
3.2.3 stack out operation
The stack is divided into left stack and right stack. Before stack, we need to judge whether the stack is empty, because if the stack is empty, no element can be out of the stack. Therefore, when the stack is empty, we throw an exception to the user, indicating that the stack is empty;
If the stack is not empty, perform the stack out operation. Save the elements to be out of the stack before moving the stack top, and then move the stack top position. The left stack top is - 1 and the right stack top is + 1; Since it is necessary to judge whether the capacity needs to be expanded when entering the stack, it is also necessary to judge whether the capacity needs to be reduced when leaving the stack. We still like ArrayList, when the number of all elements in the stack is less than or equal to 1 / 4 of the capacity of the array and the capacity of the array is greater than the initial capacity, we perform the capacity reduction operation; Finally, the saved value is returned.
public E popLeft(){
if(isLeftEmpty()){
throw new IllegalArgumentException("left stack is null");
}
E ret = data[ltop--];
if(getLeftSize()+getRightSize() <= data.length / 4 && data.length > DEFAULT_CAPACITY){
resize(data.length / 2);
}
return ret;
}
public E popRight(){
if(isRightEmpty()){
throw new IllegalArgumentException("right stack is null");
}
E ret = data[rtop++];
if(getLeftSize()+getRightSize() <= data.length / 4 && data.length > DEFAULT_CAPACITY){
resize(data.length / 2);
}
return ret;
}
3.2.4 viewing stack top elements
It is easier to view the top element of the stack. The left and right stack operations are the same. You should first judge the empty stack. If the stack is not empty, you can return to the top element of the stack. If the stack is empty, an exception will be thrown.
public E peekLeft(){
if(isLeftEmpty()){
throw new IllegalArgumentException("right stack is null");
}
return data[ltop];
}
public E peekRight(){
if(isRightEmpty()){
throw new IllegalArgumentException("right stack is null");
}
return data[rtop];
}
3.2.5 realization of expansion and contraction
Finally, it's time to expand and shrink the capacity. Both in and out of the stack need to expand and shrink the capacity, so let's implement it; The routine is similar to the expansion and contraction of ArrayList, that is, create a new array according to the given parameters, traverse the values of the original array into the new array, and then point the original array to the new array; But here are two stacks. For the left stack, we can traverse directly, while for the right stack, we need to find the relationship between the old and new array corner markers; As can be seen from the following figure, the starting index of the right stack element of the old array corresponds to the starting index of the right stack in the new array. There is a layer of relationship: index = newlen (capacity of the new array) - size (right) in the new array, that is, the number of effective elements in the right stack; The expansion capacity is the same.
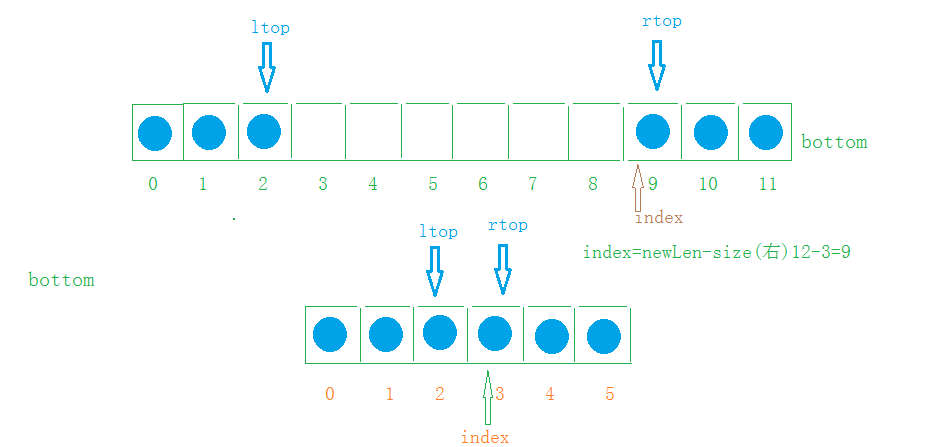
private void resize(int newLen) {
E[] newData = (E[])new Object[newLen];
for(int i = 0;i<= ltop;i++){
newData[i] = data[i];
}
int index = rtop;
for(int i = newLen - getRightSize();i<newLen;i++) {
newData[i] = data[index++];
}
rtop = newLen - getRightSize();
data = newData;
}
3.2.6 get the number of valid elements of the stack
The number of effective elements in the left stack is the top of the left stack plus 1; The number of right stack elements is the capacity of the stack minus the top of the right stack.
public int getLeftSize(){
return ltop +1;
}
public int getRightSize(){
return data.length - rtop;
}
3.2.7 air judgment
If the left stack is empty, the top of the left stack is - 1; If the right stack is empty, the top of the right stack is the capacity of the stack;
public boolean isLeftEmpty(){
return ltop == -1;
}
public boolean isRightEmpty(){
return rtop == data.length;
}
3.2.8 override toString method
When using StringBuilder, you still need to splice "[", and if the left and right stacks are empty, splice "]". If you splice the left stack first, then the right stack, splice the content in the left stack first, and then splice the content in the right stack, and then judge. If it is the last splice "]", otherwise splice "," but this is a problem. If the right stack is empty, the left stack ends with ",", This is not what we want; Therefore, we need to judge in the left stack. After splicing elements, if we traverse to ltop and the right stack is empty, splice "]" and return directly, otherwise splice ",".
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("[");
if(isLeftEmpty() && isRightEmpty()){
sb.append("]");
return sb.toString();
}
for(int i = 0;i<=ltop;i++){
sb.append(data[i]);
if(i==ltop && isRightEmpty()){
sb.append("]");
return sb.toString();
}else{
sb.append(",");
}
}
for(int i = rtop;i<data.length;i++){
sb.append(data[i]);
if(i == data.length-1){
sb.append("]");
}else{
sb.append(",");
}
}
return sb.toString();
}
3.2.9 implementing iterators
If we use ArrayList to store data, we can use the hasNext and next methods of ArrayList.
Or write an internal class and define an ArrayList and Iterator variable in the class. In the construction method, we initialize the ArrayList, traverse the elements in the stack into the ArrayList through a loop, initialize the Iterator, call the Iterator of the ArrayList, and the hasNext and next methods return the corresponding methods of the ArrayList respectively
@Override
public Iterator<E> iterator() {
return new ArrayDoubleEndStackIterator();
}
class ArrayDoubleEndStackIterator implements Iterator<E>{
private ArrayList<E> list;
private Iterator<E> it;
public ArrayDoubleEndStackIterator(){
list = new ArrayList<>();
for(int i = 0;i<=ltop;i++){
list.add(data[i]);
}
for(int i = rtop;i< data.length;i++){
list.add(data[i]);
}
it = list.iterator();
}
@Override
public boolean hasNext() {
return it.hasNext();
}
@Override
public E next() {
return it.next();
}
}
}
3.3 double ended stack test class
package test;
import linestract.ArrayDoubleEndStack;
public class ArrayDoubleEndStackTest {
public static void main(String[] args) {
ArrayDoubleEndStack<Integer> stack01 = new ArrayDoubleEndStack<>();
ArrayDoubleEndStack<Integer> stack03 = new ArrayDoubleEndStack<>();
System.out.println(stack03);
for (int i = 0; i < 10; i++) {
stack03.pushLeft(i);
stack03.pushRight(i);
}
System.out.println(stack03);
for (Integer num : stack03) {
System.out.print(num+"\t");
}
}
}
