Introduction: This article comes from the summary and record of the dark horse course, Video link . Learn data structures and algorithms. Don't memorize the results, but analyze the problem, analyze the process and implement it. The implementation method is not unique, and the idea is the positive solution.
Simple sorting
Bubble sorting
Idea:

1. Compare adjacent elements. If the former element is larger than the latter, exchange the positions of the two elements.
2. After each pair of comparison is completed, the last number is the maximum value
3. The last (0,1, 2,3...) numbers of each comparison have been compared, so there is no need to compare again
Mode 1:
public class BubbleTest {
static int arr[] = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
//Cycle arr.length times, starting at index 0
for (int i = 0; i < arr.length; i++) {
//Memory cycle comparison starts from 0, and the values of [x] and [x+1] are compared each time, and the number of internal cycles needs to be subtracted from the determined number
for (int j = 0; j < arr.length - i-1; j++) {
if (arr[j]>arr[j+1]){
int temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
System.out.println(Arrays.toString(arr));
}
}
Mode 2:
public class BubbleTest {
static int arr[] = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
for(int i=arr.length-1; i>=0 ;i--){
for (int j=0; j<i ;j++){
if (arr[j]>arr[j+1]){
int temp=arr[j+1];
arr[j+1]=arr[j];
arr[j]=temp;
}
}
}
System.out.println(Arrays.toString(arr));
}
}
The implementation method is not fixed, and the idea of problem solving is consistent.
Select sort
Idea:
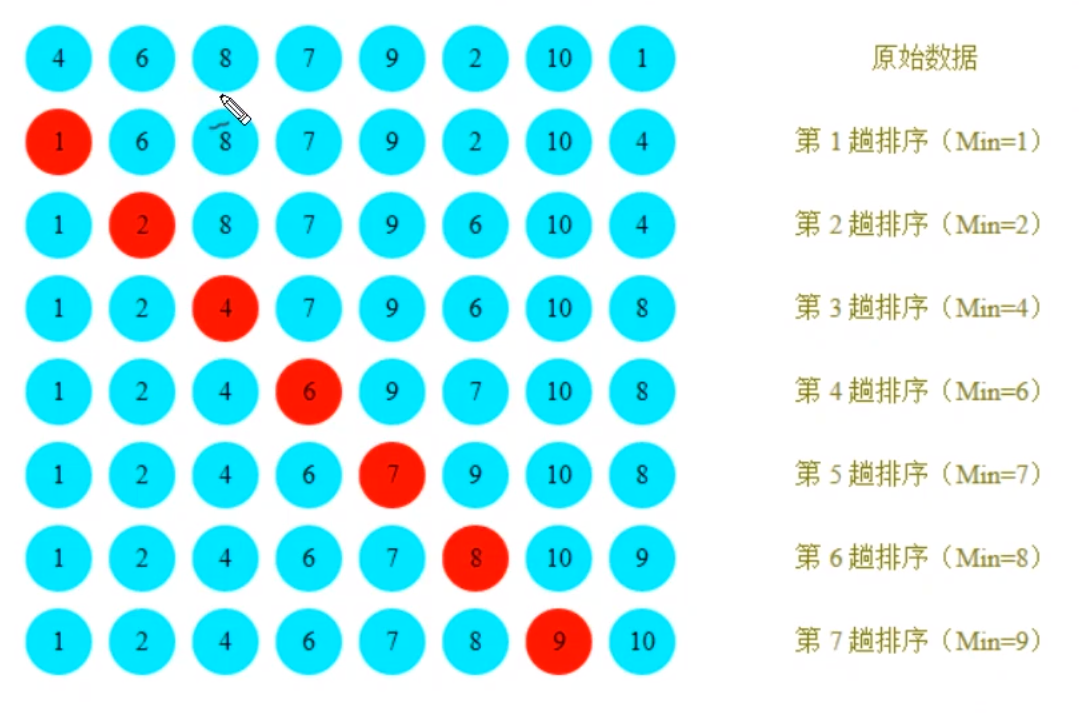
1. In the process of each traversal, it is assumed that the element at the first index is the minimum value, which is compared with the values at other indexes. If the value at the current index is greater than other index values, it is assumed that other index values are the minimum value, and finally the index where the minimum value is located can be found
2. Exchange the values at the first index and the index where the minimum value is located
3. A minimum value will be determined for each cycle
4. When the loop reaches the last time, the current index must be the minimum value, so the number of outer loops is - 1 times of array length
public class SelectTest {
static int arr[] = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
for(int i=0; i<arr.length-1; i++){
int minIndex=i;
//By default, the first index value is the minimum value, so the comparison starts from i+1
for(int j=i+1; j<arr.length;j++){
//If it is found that the assumed index value is larger than the current circular index value, replace the minimum index with the current circular index
if (arr[minIndex]>arr[j]){
minIndex=j;
}
}
//When the first index value is really the smallest value, there is no need to exchange values
if (arr[minIndex]<arr[i]){
//Exchange minimum index value and index starting value
int temp=arr[minIndex];
arr[minIndex]=arr[i];
arr[i]=temp;
}
}
System.out.println(Arrays.toString(arr));
}
}
Insert sort
Idea:
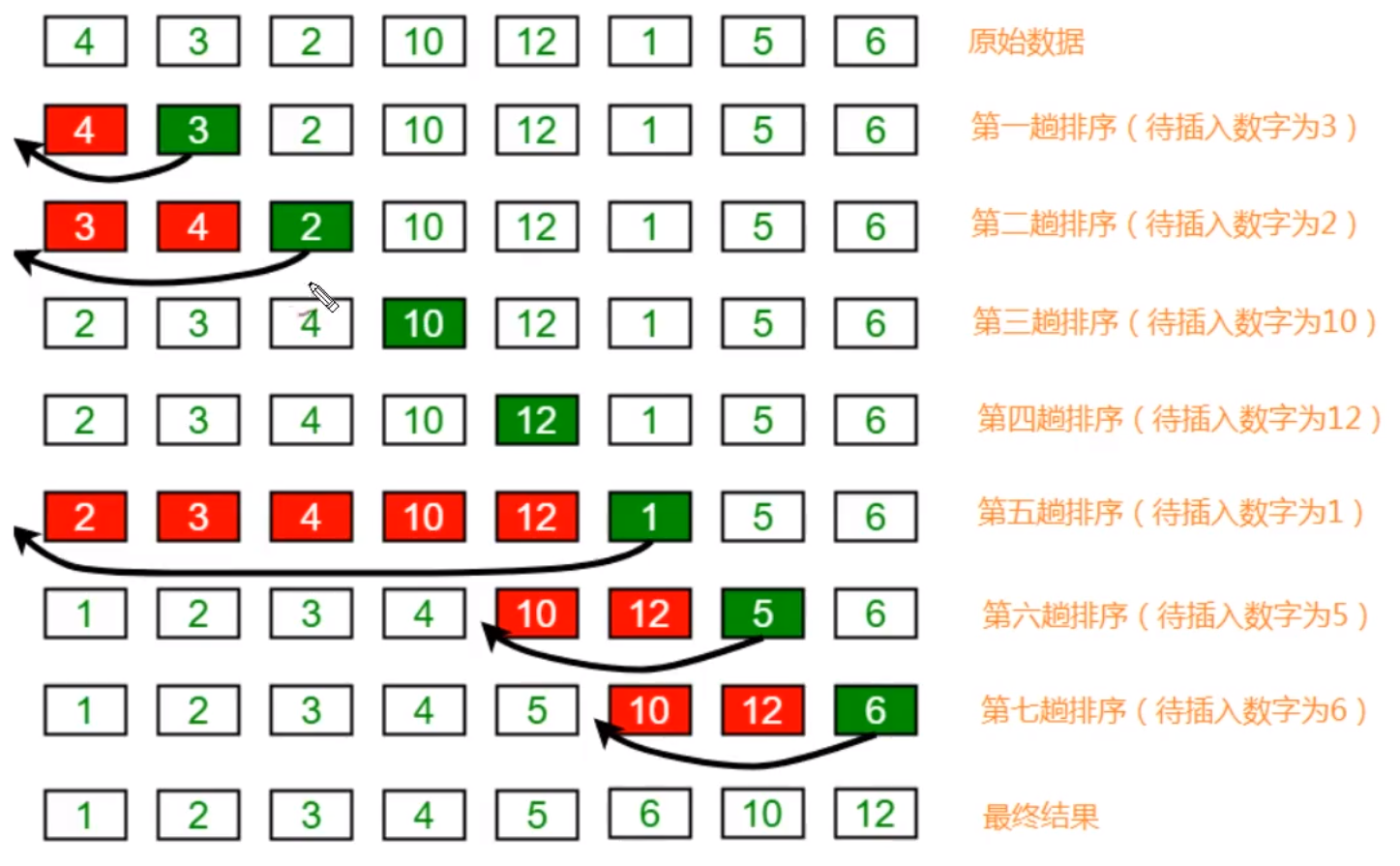
1. Divide the elements into two groups, sorted and unordered
2. The first element is sorted by default, so the completion cycle starts from 1
3. Compare the memory cycle in reverse order. When the current value is less than the next value, exchange the position. When it is greater than the next value, it is considered that the insertion place has been found, end the inner cycle and start the next outer cycle
public class InsertTest {
static int arr[] = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
//The first array is sorted by default, and the outer loop starts from 1
for (int i=1; i<arr.length; i++){
//Start the arrangement in reverse order, j is the element to be inserted, and j-1~0 is the sorted array
for(int j=i; j>0; j--){
if (arr[j]<arr[j-1]){
//If the current value is less than the next value, the position is exchanged
int temp=arr[j];
arr[j]=arr[j-1];
arr[j-1]=temp;
}else{
//Find the insertion place and end the inner loop
break;
}
}
}
System.out.println(Arrays.toString(arr));
}
}
The time complexity of the above sorting algorithms is O(n^2). With the growth of the problem scale, the time consumption increases sharply.
Advanced sorting
When the amount of data is too large, the time complexity of simple sorting increases exponentially and takes too long, so you need to learn advanced sorting
Shell Sort
Idea:
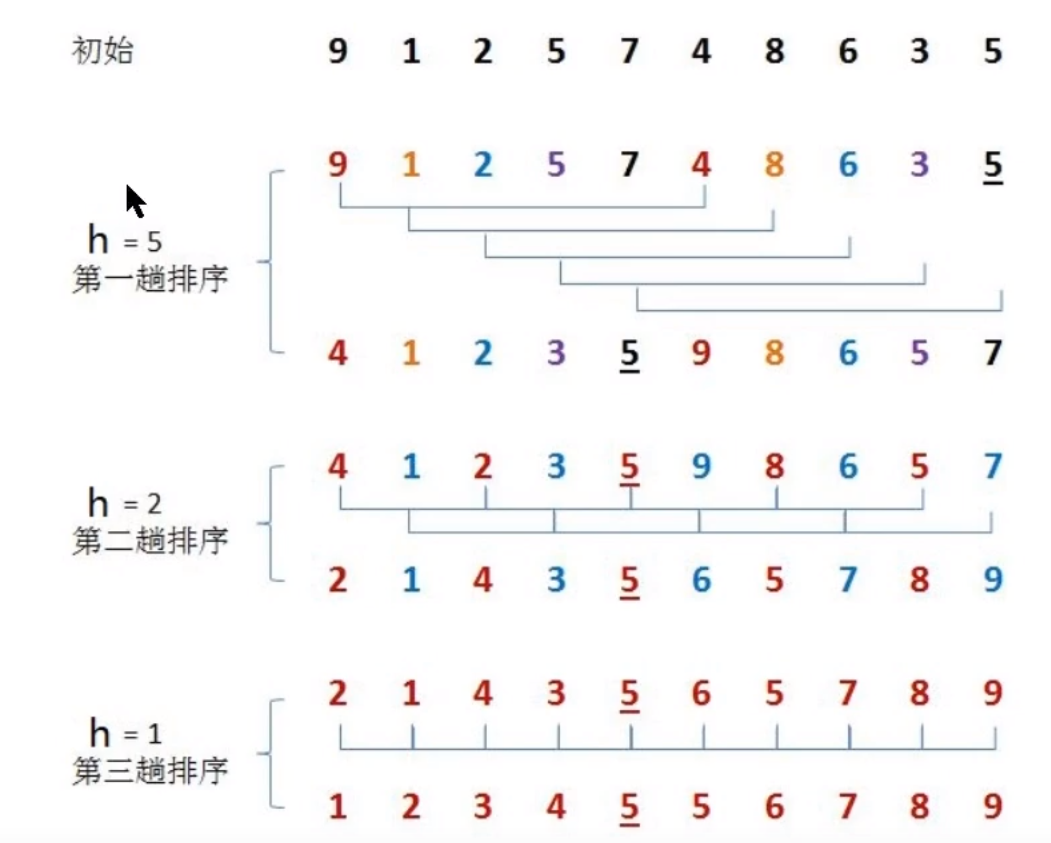
1. Hill sort can actually be regarded as an advanced version of insert sort
2. Select a growth quantity h and group the data according to the growth quantity H (for example, when h is 5, the metadata is divided into five groups - [9,4], [1,8]... [7,5], and when h is 5, it is divided into two groups [4,2,5,8,5], [1,3,9,6,7])
3. Insert and sort each group of grouped data
4. Reduce the growth, regroup, and then complete the insertion sort until h becomes 1
public class ShellTest {
static int arr[] = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
//Cycle by increment and use hill increment, that is, arr.length/2 is defined as the initial increment
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
//Group
for (int i = gap; i < arr.length; i++) {
//(gap=5, divided into 5, 6, 7, 8 and 9 according to gap. It can be inferred from the figure that subscript 5 and 0 should be a group, and 6 and 1 should be a group...)
for (int j = i; j >= gap; j -= gap) {
//According to the idea of insertion sorting, when the data to be inserted is less than the comparison data, the position is exchanged. Otherwise, it is considered that the appropriate position is found and the cycle is ended
if (arr[j] < arr[j - gap]) {
int temp = arr[j - gap];
arr[j - gap] = arr[j];
arr[j] = temp;
} else {
break;
}
}
}
}
System.out.println(Arrays.toString(arr));
}
}
Analyze and explain the code:
1. Responsible for the growth of the outer layer of gap
2. Insert and sort two for loops in the inner layer
3. Take the data in the figure as an example. When gap=5, the value range of i is 5,6,7,8,9, and the comparison contents of the inner for loop are [5,0], [6,1], [7,2], [8,3], [9,4]. The two groups of data are sorted according to insertion and replaced directly
4. When gap=2, the value of i is 2,3,4,5,6,7,8,9, and the inner loop is compared successively as [2,0], [3,1], [4,2,0], [5,3,1],... [8,6,4,2,0], [9,7,5,3,1]. From this analysis, it can be found that when i is an even number, the data can be one group, and when i is an odd number, the data is another group, namely [0,2,4,6,8], [1,3,5,7,9], and then they are inserted and sorted
Summary: Hill sort is an advanced version of insertion sort. In terms of macro grouping control, it is more troublesome to adopt the prior analysis method of algorithm, and it is more difficult to analyze because of the value problem of gap. Therefore, the post analysis method is adopted to sort with 10w reverse order data and summarize the time. It will be found that the time consumption of Hill sort is far less than that of any simple sort
Post analysis:
Hill sorting time: the result is 10 ~ 15 milliseconds
public class ShellTest {
static Integer arr[];
static ArrayList<Integer> arrayList=new ArrayList<>();
public static void main(String[] args) {
for (int i=100000; i>=0 ;i--){
arrayList.add(i);
}
arr= arrayList.toArray(new Integer[]{});
long startTime=System.currentTimeMillis();
//Cycle by increment and use hill increment, that is, arr.length/2 is defined as the initial increment
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
//Group
for (int i = gap; i < arr.length; i++) {
//(gap=5, divided into 5, 6, 7, 8 and 9 according to gap. It can be inferred from the figure that subscript 5 and 0 should be a group, and 6 and 1 should be a group...)
for (int j = i; j >= gap; j -= gap) {
//According to the idea of insertion sorting, when the data to be inserted is less than the comparison data, the position is exchanged. Otherwise, it is considered that the appropriate position is found and the cycle is ended
if (arr[j] < arr[j - gap]) {
int temp = arr[j - gap];
arr[j - gap] = arr[j];
arr[j] = temp;
} else {
break;
}
}
}
}
System.out.println(System.currentTimeMillis()-startTime);
System.out.println(Arrays.toString(arr));
}
}
Insertion sorting time: analyze the same data and the result is 21528 milliseconds
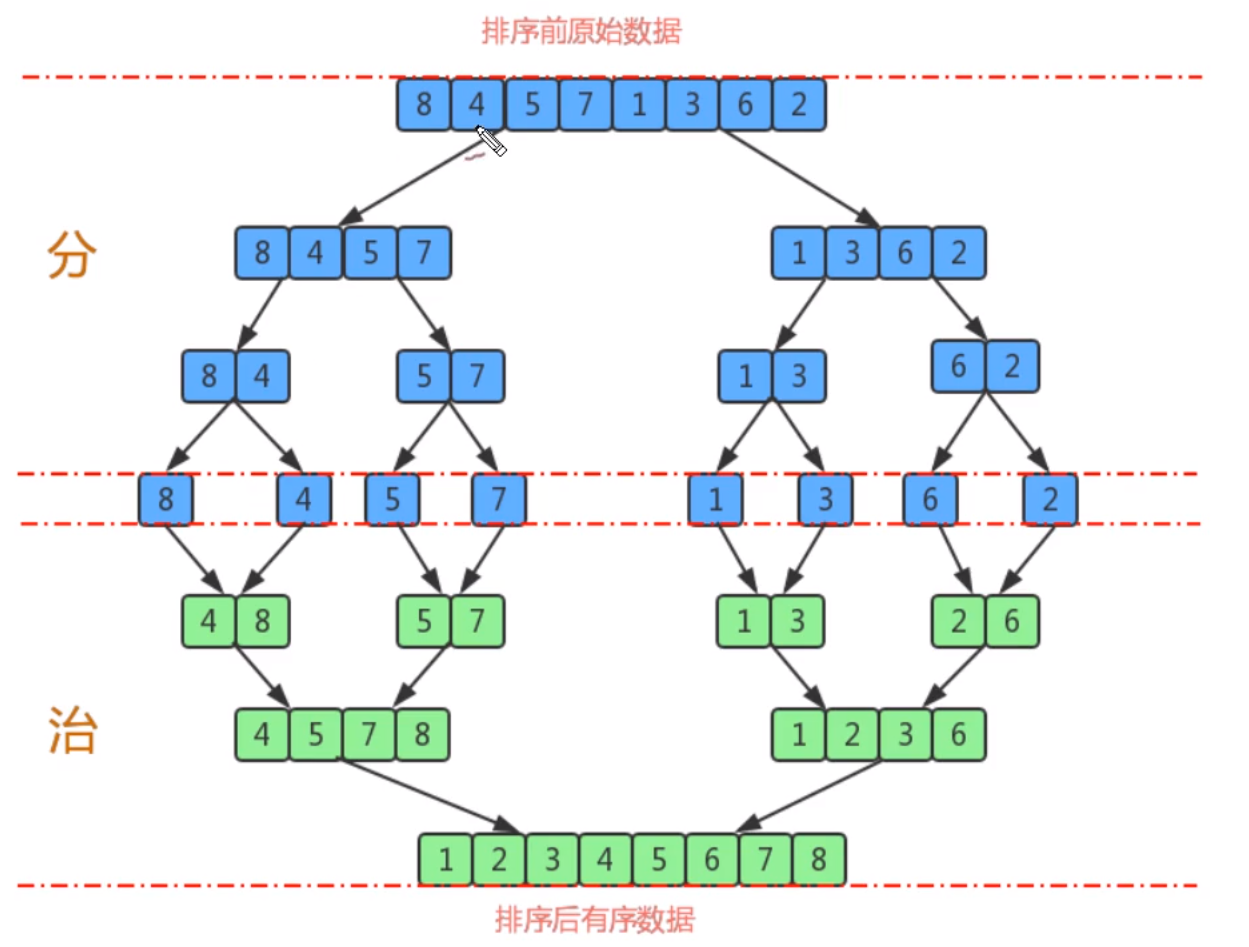
Merge sort
Idea:
1. Divide an array into two subgroups with equal elements as far as possible, and continue to split the subgroups until the number of elements of each sub tuple is 1 after splitting
2. Merge two adjacent subgroups to form an ordered large group
3. Repeat step 2
Tip from the front row: the merging and sorting is more complex. If you can't understand it, you can go and have a look at the video to explain it more clearly
public class MergeTest {
//Auxiliary array
static Integer arrs[]={10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static Integer[] assist=new Integer[arrs.length];
public static void main(String[] args) {
long startTime=System.currentTimeMillis();
//Merge start
grouping(arrs, 0, arrs.length - 1);
System.out.println(System.currentTimeMillis()-startTime);
// System.out.println(Arrays.toString(arrs));
}
//Group data
public static void grouping(Integer[] a, int start, int end) {
//Recursive termination condition
if (start >= end) {
return;
}
//Find intermediate value
int mid = start + (end - start) / 2;
//Recursive grouping
grouping(a, start, mid);
grouping(a, mid + 1, end);
//After grouping, recursively stack and merge
merge(a, start, mid, end);
}
public static void merge(Integer[] a, int start, int mid, int end) {
int pAssist = start;
int pLeft = start;
int pRight = mid + 1;
//The pointer execution interval of the left group is start mid, and the right group is mid+1-end
while (pLeft <= mid && pRight <= end) {
if (a[pLeft] < a[pRight]) {
assist[pAssist++] = a[pLeft++];
} else {
assist[pAssist++] = a[pRight++];
}
}
//There are cases where a group of pointers have reached a certain end, but the pointer on the other side has not finished, so the remaining values are directly put into the auxiliary array
while (pLeft <= mid) {
assist[pAssist++] = a[pLeft++];
}
while (pRight <= end) {
assist[pAssist++] = a[pRight++];
}
//The values in the auxiliary array have been sorted and put back into the initial array
for (int i = start; i <= end; i++) {
a[i] = assist[i];
}
}
}
Analyze and explain the code:
1. Merging is carried out recursively, so a termination condition needs to be set first, that is, the start index of the group must be less than the end index
2. To group an array, you can start with the index in the middle of the array. The index in the middle is mid = start + (end start) / 2. It doesn't matter whether the array is odd or even. Just group as much as possible
3. If an array is divided into two, they are [start, mid], [mid + 1, end]. Continue grouping the two arrays until there is only one element in the array
4. After the grouping is completed, the method frame of the virtual machine stack starts to come out of the stack for merging operation, that is, the merge method in the code
Print log to analyze recursive grouping

The results are as follows:

Analyze the results and explain them according to the calling of grouping. Only start and end variables are described here
(1). First, in the group method, you call yourself for the first time. The start of each array segmentation is start - > mid, which is understood as the left half of the array, that is:
Group (0,9) - > group (0,4) - > group (0,2) - > group (0,1) - > group (0,0) the last one satisfies start > = end, so return.
(2). The group method calls itself for the second time. Each time the array is split, the start is mid + 1 - > end, which is understood as the right half of the array. Due to the characteristics of the stack (first in, then out, last in, first out), the start, mid and end of the second call to the group method should be in the reverse order of the first call to the method stack, that is:
Group (1,1) - > if start > = end is satisfied, the method will call the merge method in the next step
Group (2,2) - > if start > = end is satisfied, the method will call the merge method in the next step
Group (3,4) - > because start > = end is not satisfied, it will enter the method loop again, that is, it will call itself again at the first call in the method, which will be reflected in the result, that is, left --start:3 end:4
According to the recursive method, all data grouping can be completed
5. Merge sorting algorithm
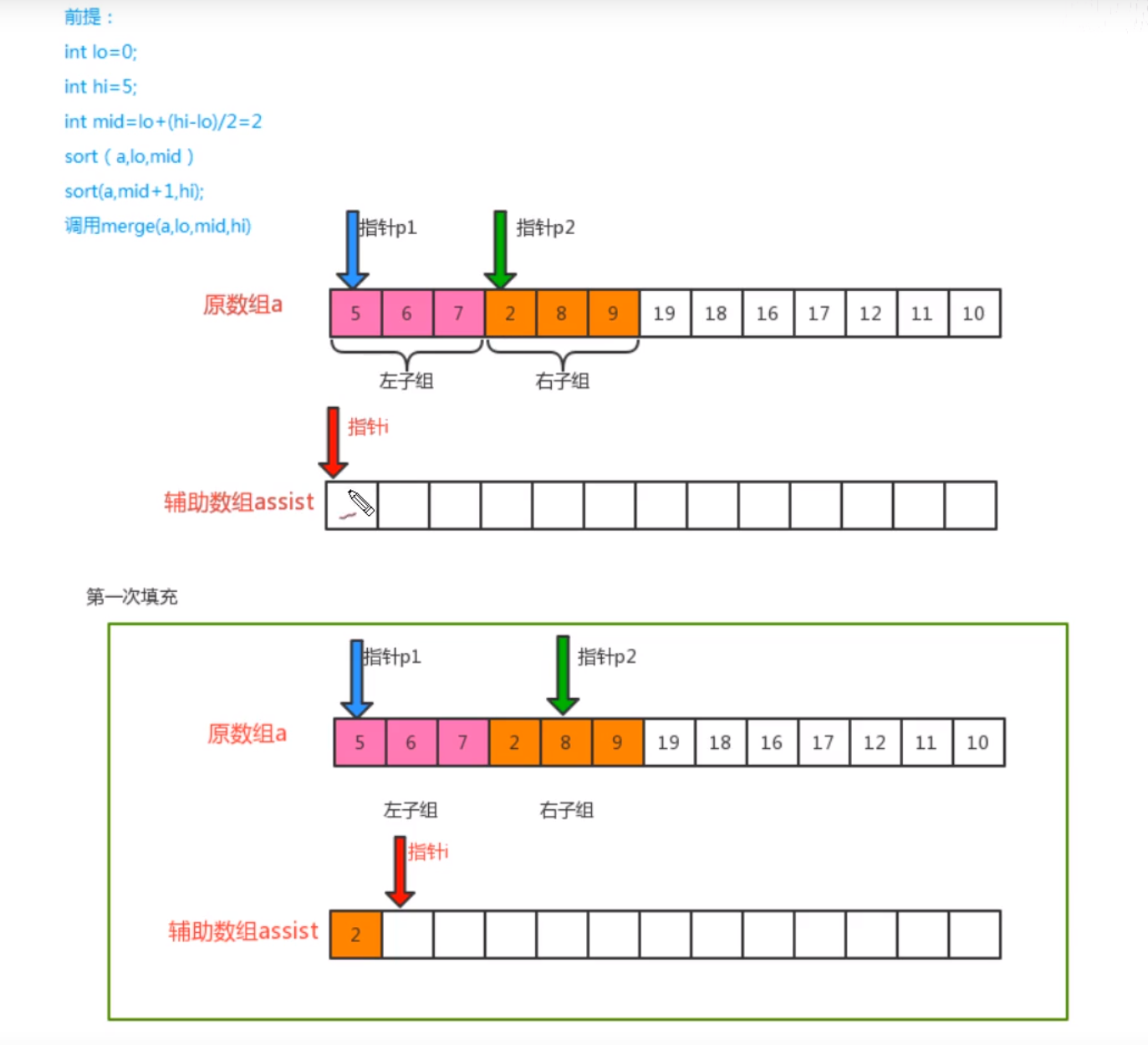
(1) The incoming array is divided into left and right arrays based on the mid intermediate quantity, and the size is compared according to the pointer respectively. The small value is put into the auxiliary array, and the small pointer position is moved back. When all the moves are completed, the loop is terminated, and the remaining array is filled into the auxiliary array. Finally, the value of the auxiliary array is overwritten into the original array
(2) From a macro perspective, because the two groups are arranged from the smallest group, the left and right arrays are always orderly within their own range, so such a comparison can be made.
Summary: merge sorting requires an auxiliary array for sorting, and recursion means that a large number of method frames will be stored in the virtual machine stack. When the number is too large, there is a risk of OOM and stack overflow. It is a typical algorithm that uses space to reduce time complexity.
Go to the back row and see the video
Quick sort
Idea:
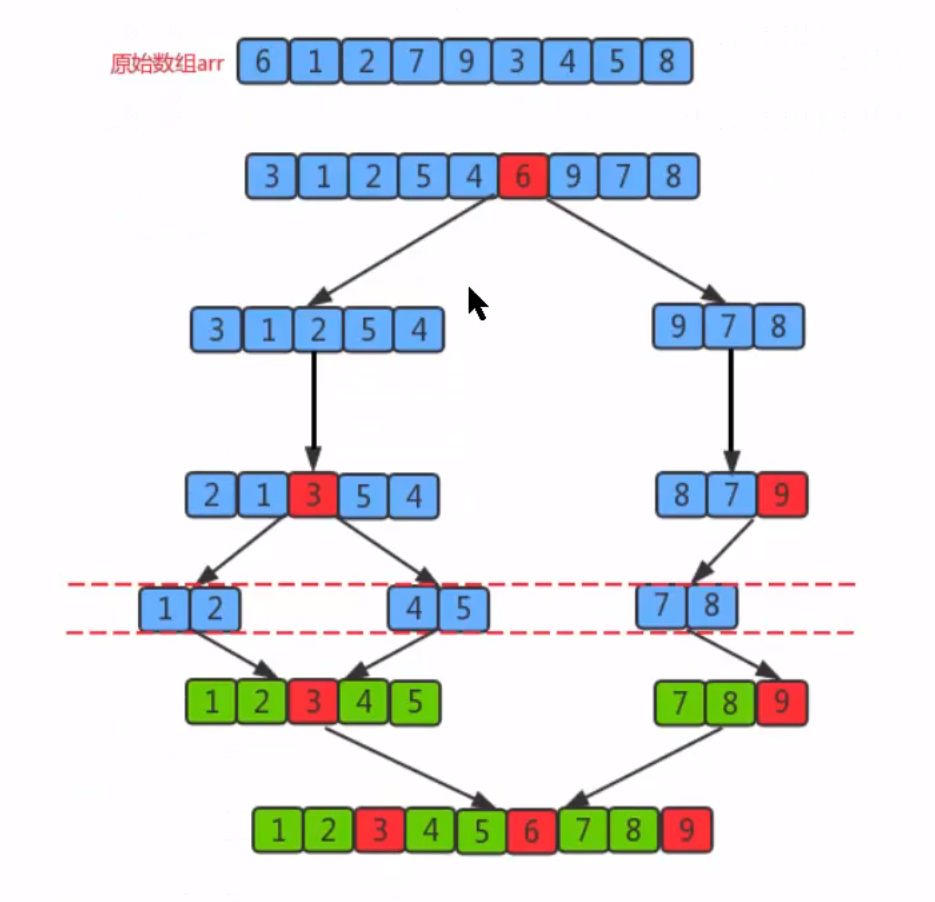
1. The quick sort algorithm adopts divide and conquer method, which is different from merge sort. It has no merging process
2. Use the first element value of the array as the boundary value, traverse the array, and put the element smaller than the boundary value on the left and the element smaller than the element on the right
3. Divide the array into left and right groups from the boundary value, and then operate them in step 2 respectively
public class QuickTest {
static int[] arrs = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
sort(arrs, 0, arrs.length - 1);
System.out.println(Arrays.toString(arrs));
}
public static void sort(int[] a, int start, int end) {
if (start >= end) {
return;
}
//Get the processed boundary value. The boundary value on the left is smaller than it, and the boundary value on the right is larger than it
int par = partition(a, start, end);
//Continue working on the separate left array
sort(a, start, par - 1);
//Continue working on the separate right-hand array
sort(a, par + 1, end);
}
//Returns the index corresponding to the boundary value
public static int partition(int[] a, int start, int end) {
//Take the first value of the array as the boundary value,
int splitNum = a[start];
//In the remaining array start end, put the value less than the limit value on the left and the value greater than the limit value on the right, and use left and right as pointers
int left = start;
int right = end + 1;
while (left < right) {
//Start with right and stop when you find an element whose value is smaller than the boundary value
while (splitNum < a[--right] && left < right) {
//This means that if the right pointer points to the header index and no suitable value is found, the loop stops
if (right == start) {
break;
}
}
//Starting from left, stop when an element with a value greater than the boundary value is found
while (splitNum > a[++left] && left < right) {
//This means that if the left pointer points to the tail index and no suitable value is found, the loop stops
if (left == end) {
break;
}
}
//When the left pointer is still smaller than the right pointer, exchange the values pointed to by the two pointers so that the value on the left is smaller than that on the right
if (left < right) {
int temp = a[left];
a[left] = a[right];
a[right] = temp;
}
}
//After sorting, the values of start and right are finally exchanged, because the values of right to the left are all less than the limit value of a[start], and the values of right to the right are all greater than a[start]
//And the final value pointed to by right must be smaller than a[start]. Exchanging a[start] and a[right] realizes grouping sorting, and right is the index of the boundary value after processing
int temp = a[start];
a[start] = a[right];
a[right] = temp;
return right;
}
}
Code interpretation:
1. In the sort method, first sort the current array, divide the value on the left of the boundary value into an array (the value on the left is smaller than the boundary value), divide the value on the right of the boundary value into an array (the value on the right is larger than the boundary value), and then recurse
2.partition method analysis:
(1). Taking array a={5, 6, 8, 9, 7, 3, 4, 1, 2} as an example, the first value of the array is set as the boundary value, that is, splitNum=a[0]=5;
(2). Define two pointers, one left pointing to the position of 5 (start) and one right pointing to the position of a.length (end+1), that is, you need to traverse and sort the {6, 8, 9, 7, 3, 4, 1, 2} array, and put the elements larger than 5 on the right of the array and the elements smaller than 5 on the left of the array
(3). Enter the while loop. When left > = right, it means that the array traversal is completed and the loop is terminated
(4). First, let the right pointer begin to decrease and find the element with the score boundary value of 5 (the element larger than 5 is on the right and does not need to move the position), and then let the left pointer start to increase step by step to find the element with the score boundary value of 5 (the element smaller than 5 is on the left and does not need to move the position). After completing a search, exchange the value pointed by the left pointer and the right pointer, That is, the sorting of values smaller than 5 and values larger than 5 is completed.
(5). When the left pointer and the right pointer are interleaved, stop the traversal. At this time, exchange the last value pointed by the original 5 and the right pointer. Then, the boundary value is placed in the appropriate place (the value on the left is less than it, and the value on the right is greater than it), and the right pointer is the index where the final boundary value 5 is located
Call the partitiond method to process the array {5, 6, 8, 9, 7, 3, 4, 1, 2} and track the process to prove the idea:

①.– right=2, less than 5, stop the right pointer movement, + left=6, greater than 5, stop the left pointer movement, at this time left is 1, right is 8, exchange a[1]=6 and a[8]=2, and get the array {5,2,8,7,3,4,1,6}
...
②. When the pointer is moved, the right pointer is now 4. Exchange the initial value with the value pointed to by right to get {3,2,1,4,5,7,8,6}. It can be observed that the values on the left side of 5 are less than it, the values on the right side are greater than it, and the index of 5 is the right value 4
The above implementation methods are easy to understand, and there are more optimized implementation methods. Those interested can baidu by themselves.