Hello everyone, I'm hehaige and focus on the back end. If I can, I want to be a code designer instead of an ordinary coder to witness the growth of hehaige. Your comments and praise are my biggest driving force. If you have any mistakes, please don't hesitate to comment. Thank you very much. Let's support the original! If there is a clerical error in pure hand typing, please forgive me.

1-1: description

☘️ Give a binary tree and verify whether it is a binary search tree. Maybe I haven't seen a binary search tree for a long time. The concept of binary search tree is not very clear. It should be emphasized here that what is a binary search tree? For any node, the nodes on the left subtree are smaller than the root node, and the nodes on the right subtree are larger than the root node. It is called a binary search tree. For example, it is very confusing that the following tree, 3, is the node on the right subtree of node 5, but 5 < 3, it is not a binary search tree.

1-2: recursion

☘️ The recursive solution is very classic, and I didn't write it successfully. The core problem is that I don't fully understand what number is a binary search tree at all, so that I think that in all nodes, the value of the left child node < the value of the right child node is a binary search tree. = = |, Wipe me. I've been fooled by Dabi! Here is the code I wrote.. At that time, I was still thinking about empty nodes until I met the above test cases..

/**
 * The concept of binary search tree is not clear. In binary search tree, all left nodes are smaller than the root and all right nodes are larger than the root
 *
 * @param root
 * @return
 */
public boolean isValidBST(TreeNode root) {
    if (root == null) {
        return true;
    }
    if (root.left == null && root.right == null) {
        return true;
    }
    if ((root.left == null && root.right.val > root.val) || (root.right == null && root.left.val < root.val)) {
        return true;
    }
    if (root.left == null || root.right == null) {
        return false;
    }
    if (root.left.val >= root.val || root.right.val <= root.val) {
        return false;
    }

    return isValidBST(root.left) && isValidBST(root.right);
}
time complexity O(N)
space complexity O(H) H It's the height of the tree

☘️ So, shall I save the minimum value of the root node? Then update the minimum value? I feel that even if it is written, the complexity is also very high. Then I looked at the comments. Someone said to use the middle order to do it. Pre saves the previous value, and I thought of a key point: the middle order traversal of the binary search tree is an increasing sequence. I just use the middle order traversal, and then use pre to record the last accessed value. Then every time I visit a node, I can use pre to compare it to ensure the overall order. So there is the following code:

public TreeNode pre = null;
public boolean isValidBST2(TreeNode root) {
    if (root == null) {
        return true;
    }
    boolean left = isValidBST2(root.left);
    if (pre != null) {
        if (root.val <= pre.val) {
            return false;
        }
    }

    pre = root;
    boolean right = isValidBST2(root.right);
    return left && right;
}

☘️ Note that it is best to write null at the beginning of pre here, because the value of the node is the minimum value of int this time. You can write it with the minimum value of long, but what do you do next time if the value is the minimum value in the number = =, so null is the best.

It's hard! Iron son.

☘️ So I took another look at the solution of the answer. Every time it traverses the child node, it uses a range to limit the child node, which is also OK. Therefore, I also adopted the interval method of opening left and opening right, as follows:

public boolean isValidBST3(TreeNode root) {
    return traverse(root, Integer.MIN_VALUE, Integer.MAX_VALUE);
}


/**
 * @param root  node
 * @param lower Left open interval
 * @param upper Right open interval
 * @return Is it a binary search tree
 */
public boolean traverse(TreeNode root, int lower, int upper) {
    if (root == null) {
        return true;
    }
    if (root.val <= lower || root.val >= upper) {
        return false;
    }
    return traverse(root.left, lower, root.val) && traverse(root.right, root.val, upper);
}

☘️ Again gg, it's still an old problem. When you meet the minimum value of int, for example: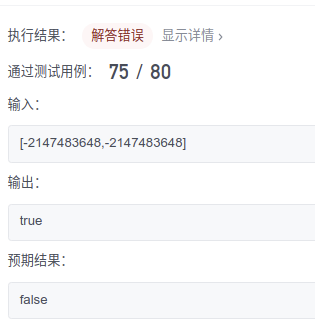
☘️ Is there a good way to limit the range other than using larger minimum and maximum values such as Long? I thought about it, like changing to a closed interval? In the case of closed interval, when the root is the minimum value, such as - 2147483648, the interval of the left child should be [- 2147483648-1]. As we all know, the minimum value of int cannot be reduced by 1, so this seems not very good. So let's use the answer method for the time being and change it to the maximum value of Long. The code is as follows:

public boolean isValidBST3(TreeNode root) {
    return traverse(root, Long.MIN_VALUE, Long.MAX_VALUE);
}


/**
 * @param root  node
 * @param lower Left open interval
 * @param upper Right open interval
 * @return Is it a binary search tree
 */
public boolean traverse(TreeNode root, long lower, long upper) {
    if (root == null) {
        return true;
    }
    if (root.val <= lower || root.val >= upper) {
        return false;
    }
    return traverse(root.left, lower, root.val) && traverse(root.right, root.val, upper);
}

1-3: iteration

☘️ Continuing the idea of middle order recursion, we write iterative Code: the iteration here still needs to be written. It's just a good time to review the non recursive writing of middle order traversal.

public boolean isValidBST4(TreeNode root) {
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    TreeNode pre = null;
    while (cur != null || !stack.isEmpty()) {
        if (cur != null) {
            stack.push(cur);
            cur = cur.left;
        } else {
            cur = stack.pop();
            if (pre == null) {
                pre = cur;
            } else {
                if (pre.val >= cur.val) {
                    return false;
                } else {
                    pre = cur;
                }
            }
            cur = cur.right;
        }
    }
    return true;
}

1-4: conclusion

☘️ The first is the definition of binary search tree:

• The left subtree of a node contains only a number smaller than the current node.
• The right subtree of a node contains only a number greater than the current node.
• All left and right subtrees themselves must also be binary search trees.

☘️ Secondly, the middle order traversal result of binary search tree is a strictly increasing sequence.

☘️ Next: there may be the minimum value of an integer in the node, which should also be taken into account. Therefore, when setting the initial value of pre, if the first node is the minimum value of the integer, it is gg.