The two players play the role of cat and mouse respectively, and play the game on an undirected graph. They take turns.

The form of graph is: graph[a] is a list, which is composed of all nodes b satisfying that ab is an edge in the graph.

The mouse starts from node 1 and starts first; The cat starts from node 2 and starts the second. There is a hole at node 0.

In each player's action, they must move along an edge connected to their current position in the graph. For example, if a mouse is at node 1, it must move to any node in the graph[1].

In addition, the cat cannot move into the hole (node 0).

Then, the game ends in one of the following three situations:

• If the cat and mouse appear at the same node, the cat wins.
• If the mouse reaches the hole, the mouse wins.
• If a position repeats (that is, the player's position and moving order are the same as the last action), the game is tied.

Give you a graph and assume that both players are participating in the game at their best:

• If the mouse wins, it returns {1;
• If the cat wins, return 2;
• Returns 0 if there is a draw.

Example 1:

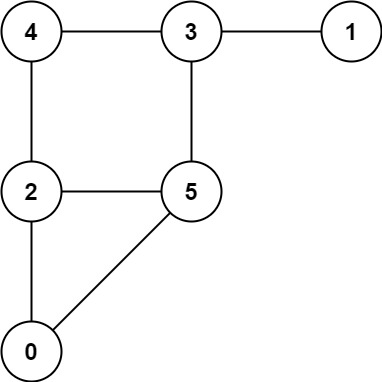
Input: graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]
Output: 0

Example 2:

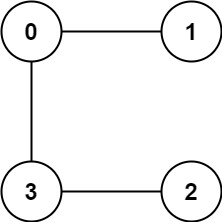
Input: graph = [[1,3],[0],[3],[0,2]]
Output: 1

Tips:

• 3 <= graph.length <= 50
• 1 <= graph[i].length < graph.length
• 0 <= graph[i][j] < graph.length
• graph[i][j] != i
• Graphs [i] are different from each other
• Cats and mice always move in the game

analysis:

Methods: dynamic programming + dfs

Considering the state and steps of the cat and mouse, and the length of the undirected graph is limited to 50, it is advisable to use three dimensions to represent the state, so that the current state is F(i, j, k), i represents the number of steps taken, j represents the node taken by the mouse, and k represents the node taken by the cat. The current state meets the following conditions:

1. When I > = twice the length of the undirected graph, it means that the cat and mouse come to a route and go back and forth, draw, F(i, j, k) = 0
2. When j = 0, the mouse enters the hole, the mouse wins, F(i, j, k) = 1
3. When j = k ， the cat and the mouse meet. The cat wins. F(i, j, k) = 2

The priority of the mouse is: hole > Draw > cat. The priority of the cat is: don't let the mouse enter the hole > catch the mouse > draw. We can use depth first traversal and judge according to the priority. Because the mouse goes first, and we start from 0, so we take the remainder of the steps. The even number is the old mouse step and the odd number is the cat step.

Time complexity: O(n^4)
Space complexity: O(n^3)

class Solution {

    //Undirected graph
    int[][] graph;
    //Define 3D array
    int[][][] arr;
    //The maximum number of nodes is 50
    int num = 50;

    public int catMouseGame(int[][] graph) {
        this.graph = graph;
        //Define 3D array
        arr = new int[num * 2][num][num];
        //Traversal. The array defaults to 0. Returning - 1 means a draw
        int res = dfs(0, 1, 2);
        return res == -1? 0: res;
    }

    public int dfs(int i, int j, int k){
        //Repeated traversal once, draw
        if(i == num * 2){
            return -1;
        }
        //The mouse goes into the hole
        if(j == 0){
            arr[i][j][k] = 1;
            return 1;
        }
        //The cat caught the mouse
        if(j == k){
            arr[i][j][k] = 2;
            return 2;
        }
        //walk
        if(arr[i][j][k] != 0){
            return arr[i][j][k];
        }
        //Mouse step
        if(i % 2 == 0){
            //Logo cat wins
            int cat = 2;
            //Traversal route
            for(int g: graph[j]){
                //Off road condition
                int state = dfs(i+1, g, k);
                //There's a hole. Go in
                if(state == 1){
                    arr[i][j][k] = 1;
                    return 1;
                }
                //The cat can't win a draw
                if(state == -1){
                    cat = -1;
                }
            }
            arr[i][j][k] = cat;
            return cat;
        }
        //Catwalk
        //Logo mouse wins
        int mouse = 1;
        //Traversal route
        for(int g: graph[k]){
            //Rat hole, no entry
            if(g == 0){
                continue;
            }
            //Off road condition
            int state = dfs(i+1, j, g);
            //Catch a mouse
            if(state == 2){
                arr[i][j][k] = 2;
                return 2;
            }
            //Draw, mouse can't win
            if(state == -1){
                mouse = -1;
            }
        }
        arr[i][j][k] = mouse;
        return mouse;
    }
}

Title Source: LeetCode
Link: https://leetcode-cn.com/problems/cat-and-mouse