Tip: after the article is written, the directory can be generated automatically. Please refer to the help document on the right for how to generate it
1, Algorithm implementation
1. Bubble sorting
1) . compare all elements in the sequence in pairs and put the smallest one at the front;
2) . compare all elements in the remaining sequence in pairs, and put the smallest one at the front;
3) . repeat step 2 until only one number is left.
The code is as follows (example):
import java.util.Arrays;
public class BubbleSortDemo {
public static void main(String[] args) {
int[] array = {1, 4, 2, 8, 5, 7, 3, 6, 9, 0};
System.out.println(Arrays.toString(array));
bubbleSort(array);
System.out.println(Arrays.toString(array));
}
private static void bubbleSort(int[] arr) {
boolean flag = true;
for(int i = 0; i < arr.length && flag; i++) {
flag = false;
for(int j = arr.length - 1; j > i; j--) {
//For the bubbling of the upgraded version, the best time complexity can be O(n)
if(arr[j] < arr[j - 1]) {
int temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
flag = true;
}
}
}
}
private static void bubbleSortOld(int[] arr) {
for(int i = 0; i < arr.length - 1; i++) {
for(int j = i + 1; j < arr.length; j++) {
//The most basic bubbling, even if ordered, has a time complexity of O(n) ²)
if(arr[i] > arr[j]) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
}
}
}
Time complexity (average): O(n) ²) time complexity (best): O(n) time complexity (worst): O(n) ²)
Spatial complexity: O(1) stability: stability
2. Select Sorting
1. Traverse the whole sequence and put the smallest number in front;
2. Traverse the remaining sequences and put the smallest number at the front;
3. Repeat step 2 until there is only one number left.
The code is as follows (example):
import java.util.Arrays;
public class SelectionSortDemo {
public static void main(String[] args) {
int[] array = {1, 4, 2, 8, 5, 7, 3, 6, 9, 0};
System.out.println(Arrays.toString(array));
selectionSort(array);
System.out.println(Arrays.toString(array));
}
private static void selectionSort(int[] arr) {
for(int i = 0; i < arr.length - 1; i++) {
int min = i;
for(int j = i + 1; j < arr.length; j++) {
if(arr[j] < arr[min]) min = j;
}
if(min != i) {
int temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}
}
}
Time complexity (average): O(n) ²) time complexity (best): O(n) ²) time complexity (worst): O(n) ²)
Spatial complexity: O(1) stability: instability
3. Insert sort
1. Sort the first element and the second element, and then form an ordered sequence;
2. Insert the third element to form a new ordered sequence;
3. Repeat step 2 for the fourth element, the fifth element... Until the last number.
The code is as follows (example):
import java.util.Arrays;
public class InsertSortDemo {
public static void main(String[] args) {
int[] array = {1, 4, 2, 8, 5, 7, 3, 6, 9, 0};
System.out.println(Arrays.toString(array));
insertionSort(array);
System.out.println(Arrays.toString(array));
}
private static void insertionSort(int[] arr) {
for(int i = 0; i < arr.length - 1; i++) {
for(int j = i + 1; j > 0; j--) {
//If the current element is smaller than the previous element, it is swapped
if(arr[j] >= arr[j - 1]) break;
int temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
}
}
}
}
Time complexity (average): O(n) ²) time complexity (best): O(n) time complexity (worst): O(n) ²)
Spatial complexity: O(1) stability: stability
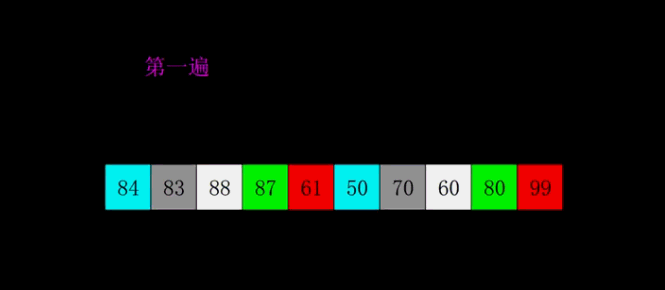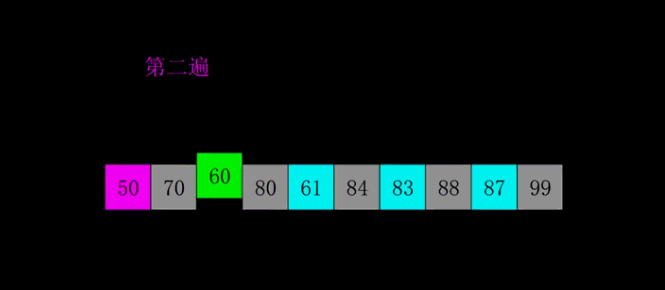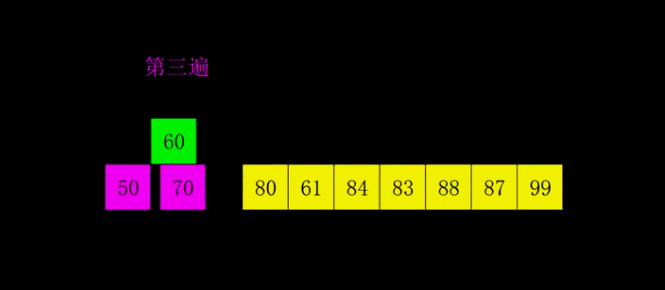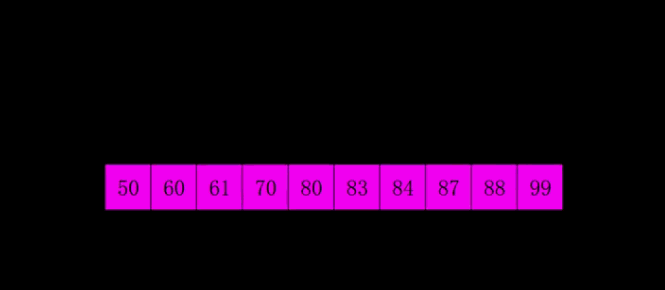
4. Hill sort
1. Set the number of elements as N, take the odd number k=n/2, and divide the elements with subscript difference K into a group to form an ordered sequence;
2. Take k=k/2 and divide the elements with subscript difference of K into a group to form an ordered sequence;
3. Repeat step 2 until k=1 performs a simple insertion sort.
The code is as follows (example):
import java.util.Arrays;
public class ShellSortDemo {
public static void main(String[] args) {
int[] array = {1, 4, 2, 8, 5, 7, 3, 6, 9, 0};
System.out.println(Arrays.toString(array));
shellSort(array);
System.out.println(Arrays.toString(array));
}
private static void shellSort(int[] arr) {
for(int gap = arr.length / 2; gap > 0; gap /= 2) {
for(int j = 0; (j + gap) < arr.length; j++) {
for(int k = 0; (k + gap) < arr.length; k += gap) {
if(arr[k] > arr[k + gap]) {
int temp = arr[k + gap];
arr[k + gap] = arr[k];
arr[k] = temp;
}
}
}
}
}
}
Time complexity (average): O(n^1.3) time complexity (best): O(n) time complexity (worst): O(n) ²)
Spatial complexity: O(1) stability: instability
5. Quick sort
1. Select the first number as P, the number less than p is placed on the left, and the number greater than p is placed on the right;
2. Recursively carry out the numbers on the left and right of p according to the first step until recursion cannot be carried out.
The code is as follows (example):
import java.util.Arrays;
public class QuickSortDemo {
public static void main(String[] args) {
int[] array = {1, 4, 2, 8, 5, 7, 3, 6, 9, 0};
System.out.println(Arrays.toString(array));
quickSort(array, 0, array.length - 1);
System.out.println(Arrays.toString(array));
}
private static void quickSort(int[] array, int left, int right) {
if(left > right) return;
int i = left, j = right, base = array[left];
while(i < j) {
while(i < j && array[j] > base) j--;
while(i < j && array[i] <= base) i++;
if(i < j) swap(array, i, j);
}
swap(array, i, left);
quickSort(array, left, i - 1);
quickSort(array, i + 1, right);
}
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
Time complexity (average): O(nlogn) time complexity (best): O(nlogn) time complexity (worst): O(n ²)
Spatial complexity: O(logn) stability: instability
6. Merge and sort
1. Select two adjacent numbers to form an ordered sequence;
2. Select two adjacent ordered sequences to form an ordered sequence;
3. Repeat step 2 until all become an ordered sequence.
The code is as follows (example):
import java.util.Arrays;
public class MergeSortDemo {
public static void main(String[] args) {
int[] array = {1, 4, 2, 8, 5, 7, 3, 6, 9, 0};
System.out.println(Arrays.toString(array));
mergeSort(array, 0, array.length - 1);
System.out.println(Arrays.toString(array));
}
private static void mergeSort(int[] array, int start, int end) {
if(start < end) {
int mid = (start + end) / 2;
mergeSort(array, start, mid);
mergeSort(array, mid + 1, end);
merge(array, start, mid, end);
}
}
private static void merge(int[] array, int left, int mid, int right) {
int[] temp = new int[array.length];
int p1 = left, p2 = mid + 1, k = left;
while(p1 <= mid && p2 <= right) {
if(array[p1] <= array[p2]) temp[k++] = array[p1++];
else temp[k++] = array[p2++];
}
while(p1 <= mid) temp[k++] = array[p1++];
while(p2 <= right) temp[k++] = array[p2++];
for(int i = left; i <= right; i++) {
array[i] = temp[i];
}
}
}
Time complexity (average): O(nlogn) time complexity (best): O(nlogn) time complexity (worst): O(nlogn)
Spatial complexity: O(n) stability: stability
7. Heap sorting
1. Build the sequence into a large top stack;
2. Exchange the root node with the last node, and then disconnect the last node;
3. Repeat steps 1 and 2 until all nodes are disconnected.

The code is as follows (example):
import java.util.Arrays;
public class HeapSortDemo {
public static void main(String[] args) {
int[] array = {1, 4, 2, 8, 5, 7, 3, 6, 9, 0};
System.out.println(Arrays.toString(array));
heapSort(array);
System.out.println(Arrays.toString(array));
}
private static void heapSort(int[] array) {
//1. Build large top reactor
for(int i = array.length / 2 - 1; i >= 0; i--) {
//Adjust the structure from a non leaf node from bottom to top and from right to left
adjustHeap(array, i, array.length);
}
//2. Exchange the top and end elements of the heap and adjust the heap structure
for(int j = array.length - 1; j > 0; j--) {
swap(array, 0, j);
adjustHeap(array, 0, j);
}
}
private static void adjustHeap(int[] array, int i, int length) {
int temp = array[i];
//Start from the left child of node i, that is, 2i + 1
for(int k = i * 2 + 1; k < length; k = k * 2 + 1) {
//If the left child node is smaller than the right child node, k points to the right child node
if(k + 1 < length && array[k] < array[k + 1]) k++;
if(array[k] > temp) { //If the child node is larger than the parent node, assign the child node to the parent node
array[i] = array[k];
i = k;
} else break;;
}
array[i] = temp;
}
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
Time complexity (average): O(nlogn) time complexity (best): O(nlogn) time complexity (worst): O(nlogn)
Spatial complexity: O(1) stability: instability
8. Cardinality sorting
1. Take out the single digits of all numbers and sort them according to the single digits to form a sequence;
2. Take out the ten digits of all newly formed numbers and sort them according to the ten digits to form a sequence;
3. Repeat until the maximum number of digits.

The code is as follows (example):
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class BasicSortDemo {
public static void main(String[] args) {
int[] array = {1, 4, 2, 8, 5, 7, 3, 6, 9, 0};
System.out.println(Arrays.toString(array));
basicSort(array);
System.out.println(Arrays.toString(array));
}
private static void basicSort(int[] array) {
List<ArrayList<Integer>> dyadic = new ArrayList<>();
for(int i = 0; i < 10; i++) {
ArrayList<Integer> arr = new ArrayList<>();
dyadic.add(arr);
}
int max = 0;
for (int item : array) {
if (item > max) max = item;
}
int times = 0;//Determine the maximum number of digits, which is the number of cycles
while(max > 0) {
max /= 10;
times++;
}
for(int i = 0; i < times; i++) {
for (int value : array) {
int x = value % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
//Take the array as a subscript, find the corresponding sub array, add the element to the sub array, and update the large array
ArrayList<Integer> arr = dyadic.get(x);
arr.add(value);
dyadic.set(x, arr);
}
}
int index = 0; //Traverse the subarray in turn and add the elements in each subarray to the array
for(int k = 0; k < 10; k++) {
while(dyadic.get(k).size() > 0) {
ArrayList arr = dyadic.get(k);
array[index] = (int)arr.get(0);
arr.remove(0);
index++;
}
}
}
}
Time complexity (average): O(nk) time complexity (best): O(nk) time complexity (worst): O(n*k)
Spatial complexity: O(n+k) stability: stability
2, Stability analysis
Stability of sorting algorithm: in the sequence to be sorted, there are the same elements. After sorting, the relative position of the same elements remains unchanged. For example, in the original sequence, r[i]=r[j], and r[i] is before r[j], while in the sorted sequence, r[i] is still before r[j]. This sorting algorithm is stable.
1. Bubble sorting
Bubble sort is to move the small elements forward or to move the big elements back. Compared to the comparison between the two adjacent elements, the exchange occurs between the two elements. The two elements are equal, so they do not exchange places; if two equal elements are not adjacent, even if 22 exchanges are two adjacent, this time will not be exchanged again, so the same elements are in order. There is no change, so bubble sorting is a stable sorting algorithm.
2. Select Sorting
Selection sorting is to select the smallest element for each position. For example, select the smallest element for the first position, select the second smallest element for the second element among the remaining elements, and so on. In one selection, if the current element is smaller than an element, and the small element appears behind an element equal to the current element, the stability after exchange will be destroyed For example, in sequence 5 8 5 2 9, if the first element 5 is selected for the first time, it will exchange with 2, then the relative sequence of the two 5 in the original sequence will be destroyed, so selective sorting is not a stable sorting algorithm.
3. Insert sort
Insertion sorting is to insert one element at a time on the basis of an ordered small sequence. The comparison starts from the end of the ordered sequence, that is, the element you want to insert is compared with the largest one that has been ordered. If it is larger than it, it is directly inserted behind it. Otherwise, look forward until you find its insertion position. If you encounter an element that is equal to the inserted element, the inserted element puts the element you want to insert after the equal element. Therefore, the sequence of equal elements has not changed. The order out of the original unordered sequence is the order after the order is arranged, so the insertion sort is stable.
4. Hill sort
Hill sort is to insert and sort elements according to asynchronous length. One insertion sort is stable and does not change the relative order of the same elements. Due to multiple insertion sorts, the same elements may move in their insertion sorts in different insertion sorts, and finally their stability will be disturbed. Therefore, Hill sort is unstable.
5. Quick sort
There are two directions for quick sorting. The I subscript on the left always goes to the right. When a[i] < = a[center_index], where center_ Index is the array index of the central element, which is generally taken as the 0th element of the array. The j subscript on the right goes all the way to the left when a[j] > a[center_index]. If I and J can't move, I < = J, exchange a[i] and a[j], and repeat the above process until I > J. Exchange a[j] and a[center_index] to complete a quick sort. When the central element is exchanged with a[j], it is likely to disrupt the stability of the previous elements. For example, the sequence is 5 3 3 4 3 8 9 10 11. Now the exchange of central elements 5 and 3 (the fifth element, the subscript starts from 1) will disrupt the stability of element 3. Therefore, quick sorting is an unstable sorting algorithm. Instability occurs when the central element is exchanged with a[j].
6. Merge and sort
Merge sort is to recursively divide the sequence into short sequences. The recursive exit is that the short sequence has only one element (considered as direct order) or two elements (one comparison and exchange), and then merge each ordered segment sequence into an ordered long sequence, and continue to merge until all the original sequences are in order. There is no exchange in one element, and there is no need to exchange two elements if they are equal in size, so it will not destroy the stability. In the merging process, we can ensure that if the two current elements are equal, the elements of the previous sequence are saved in front of the result sequence, so as to ensure stability. Therefore, merge sorting is also a stable sorting algorithm.
7. Heap sorting
The structure of the heap is that the children of node i are 2i and 2i+1 nodes. The large top heap requires that the parent node be greater than or equal to its 2 child nodes, and the small top heap requires that the parent node be less than or equal to its 2 child nodes. In a sequence with a length of N, the heap sorting process starts from n/2 and selects the maximum (large top heap) or minimum (small top heap) with a total of three values of its child nodes. Of course, the selection between these three elements will not destroy the stability. However, when selecting elements for the parent nodes n/2-1, n/2-2,... 1, the stability will be destroyed. It is possible that the n/2 parent node exchanges the following element, while the n/2-1 parent node does not exchange the following same element, then the stability between the two same elements will be destroyed. Therefore, heap sorting is not a stable sorting algorithm.
8. Cardinality sorting
Cardinality sorting is sorting according to the low order, and then collecting; Then sort according to the high order, and then collect; And so on until the highest order. Cardinality sorting is based on sorting separately and collecting separately. The same elements do not need to be sorted and the sequence will not be changed, so it is a stable sorting algorithm.
Stability summary
Stable sorting algorithm: bubble sort, insert sort, merge sort and cardinal sort
Unstable sorting algorithm: selective sorting, quick sorting, Hill sorting and heap sorting