Reprinted please indicate the source!
I. concept
Balanced Binary Tree is a special Binary Search Tree. For Binary Search Tree, please check the previous blog. java implementation of binary search tree What's special about binary search tree? It's clear to understand the basic of binary search tree. Inserting values into binary search tree sequentially will eventually form a tree similar to a linked list. The original intention of designing binary search tree is obviously to see that its search speed is proportional to its height. If every binary tree is like a linked list, it's unintentional. So we designed the balanced binary tree. Compared with the binary search tree, one of the characteristics of the balanced binary tree is that the absolute value of the difference between left and right subtrees of any node in the tree must be less than 2. For the evolution of what, please search the answer online by yourself. In this paper, for convenience, int value insertion is also used.
II. Construction of Balanced Binary Tree
Compared with binary search tree, its classes have nothing special, so they can be directly coded without too much explanation.
1 static class Node{ 2 Node parent; 3 Node leftChild; 4 Node rightChild; 5 int val; 6 public Node(Node parent, Node leftChild, Node rightChild,int val) { 7 super(); 8 this.parent = parent; 9 this.leftChild = leftChild; 10 this.rightChild = rightChild; 11 this.val = val; 12 } 13 14 public Node(int val){ 15 this(null,null,null,val); 16 } 17 18 public Node(Node node,int val){ 19 this(node,null,null,val); 20 } 21 22 }
Increase
When we talk about the increase of balanced binary trees, we should first consider what kind of situation will break the balance. If A tree is already a balanced binary tree, but now we need to insert an element into it. There are two results. First, the balance is not broken. This must be great joy. Second, the balance is broken. There are generally three issues to consider.
First, what was the state before the balance was broken?
Second, what kind of state is it after being broken?
3. The balance has been broken. How can we adjust it so that it can become a balanced binary tree again?
Here we intercept all possible cases where the height of the left subtree is 2 higher than the height of the right subtree after breaking the balance (if the right subtree is high, as is the case, only one analysis is selected here). The following figure only represents the subtree of the breaking equilibrium point (the breaking equilibrium point is that the absolute value of the height difference between the left subtree and the right subtree of the node is greater than or equal to 2, of course, here only equals 2). Represents the whole tree.
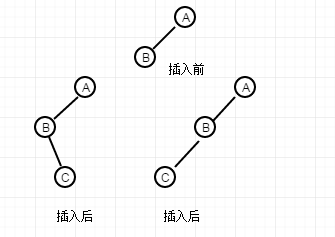
This is the first case, where A node and B node are only a subset of the balanced binary tree. To break this balance, the inserted node C must be on the sub-node of B, that is, the left and right sub-nodes.
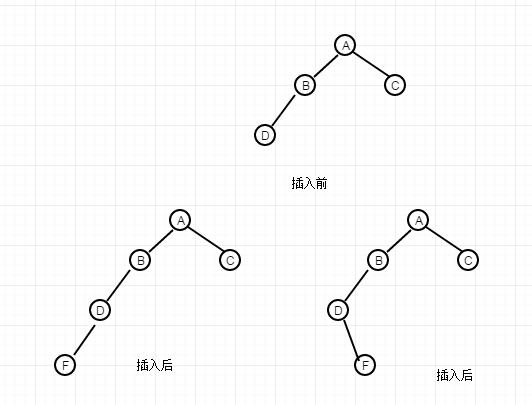
This is the second case, in which A, B, C and D nodes are also a subset of the equilibrium tree. To break the balance, the inserted node F must be on the D node.
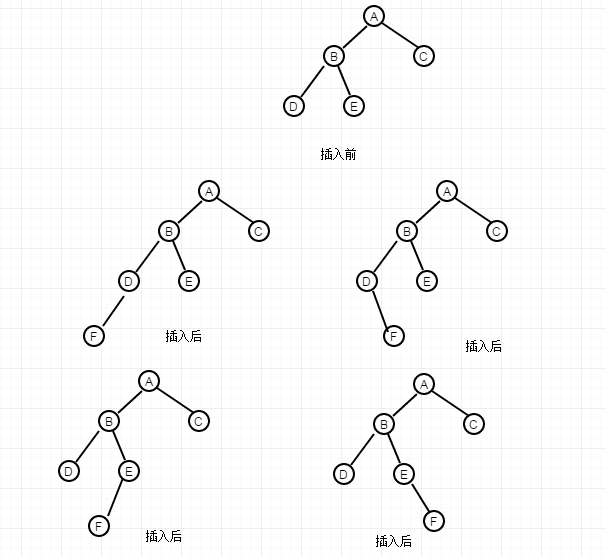
In the third case, the five nodes A, B, C, D and E are also a subset of the equilibrium tree. To break the balance, the inserted node F must be on the D and E nodes.
(If there are any other possible scenarios that I think of personally, please point them out in the comments. Thank you! )
Perhaps careful people have found that the second and third scenarios are derived from the first scenario, such as adding child nodes to the right children of node A and B respectively, which changes to the second and third scenarios (this does not mean that the first scenario directly adds these nodes to the second or third scenario).
Only the first case is analyzed in detail here.
In order to make the absolute value of the difference between left and right subtrees of A node less than 2, only B node is replaced by A node, A node becomes the right child of B node. If A node has a parent node, then the child node of A's parent node should point to B node, and the parent node of A node should point to B node. Look at this code first. This operation is a right-handed operation.
1 /** 2 * In this case, because both A and B nodes have no right child nodes, 3 * So don't think too much about it. 4 * @param aNode Represents node A 5 * @return 6 */ 7 public Node leftRotation(Node aNode){ 8 if(aNode != null){ 9 Node bNode = aNode.leftChild;// Store with a variable first B node 10 bNode.parent = aNode.parent;// Redistribution A Parent Point of a Node 11 //judge A Whether the parent node of a node exists 12 if(aNode.parent != null){// A Nodes are not root nodes 13 /** 14 * In two cases 15 * 1,A If the node is located on the left of its parent node, then the B node is also located on the left. 16 * 2,A If the node is located on the right of its parent node, then the B node is also located on the right. 17 */ 18 if(aNode.parent.leftChild == aNode){ 19 aNode.parent.leftChild = bNode; 20 }else{ 21 aNode.parent.rightChild = bNode; 22 } 23 }else{// Explain A The node is the root node, directly B The node is set to the root node 24 this.root = bNode; 25 } 26 bNode.rightChild = aNode;// take B The right child of the node is set to A node 27 aNode.parent = bNode;// take A The parent of the node is set to B node 28 return bNode;// Returns the rotating node 29 } 30 return null; 31 }
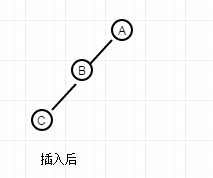
And for the first case, the graph
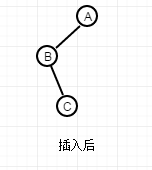
The situation involved is different. If you go right-handed as in the above case, the figure you get may be like this.
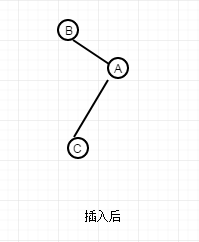
This seems to be unbalanced. It seems to be symmetrical with the original graph. Not very practical. If C node is replaced by B node, and B node becomes the left node of C node, this becomes the case of the previous code. The code for replacing this B node with a C node is as follows, which is to do left-handed and right-handed first.
1 /** 2 * 3 * @param bNode Represents B node 4 * @return 5 */ 6 public Node rightRotation(Node bNode){ 7 if(bNode != null){ 8 Node cNode = bNode.rightChild;// Store with temporary variables C node 9 cNode.parent = bNode.parent; 10 // Here because bNode Node parent exists, so no judgment is needed. Judgment will do., 11 if(bNode.parent.rightChild == bNode){ 12 bNode.parent.rightChild = cNode; 13 }else{ 14 bNode.parent.leftChild = cNode; 15 } 16 cNode.leftChild = bNode; 17 bNode.parent = cNode; 18 return cNode; 19 } 20 return null; 21 }
The code logic is the same as the previous code. After the transformation, and then according to the above right-handed operation again, it becomes a balance tree.
For the analysis of the second and third cases and the similarity of the first case, we can modify the code to suit the three cases. The complete code is as follows.
1 public Node rightRotation(Node node){ 2 if(node != null){ 3 Node leftChild = node.leftChild;// Store with variables node Left child node of node 4 node.leftChild = leftChild.rightChild;// take leftChild The right child of the node is assigned to node Left node of node 5 if(leftChild.rightChild != null){// If leftChild If the right node exists, the parent of the right node needs to be assigned to node node 6 leftChild.rightChild.parent = node; 7 } 8 leftChild.parent = node.parent; 9 if(node.parent == null){// That is to say node The node is the root node 10 this.root = leftChild; 11 }else if(node.parent.rightChild == node){// Namely node The node is in the right subtree of its original parent 12 node.parent.rightChild = leftChild; 13 }else if(node.parent.leftChild == node){ 14 node.parent.leftChild = leftChild; 15 } 16 leftChild.rightChild = node; 17 node.parent = leftChild; 18 return leftChild; 19 } 20 return null; 21 }
Above is the right-handed code. Logical reference to the above analysis
1 public Node leftRotation(Node node){ 2 if(node != null){ 3 Node rightChild = node.rightChild; 4 node.rightChild = rightChild.leftChild; 5 if(rightChild.leftChild != null){ 6 rightChild.leftChild.parent = node; 7 } 8 rightChild.parent = node.parent; 9 if(node.parent == null){ 10 this.root = rightChild; 11 }else if(node.parent.rightChild == node){ 12 node.parent.rightChild = rightChild; 13 }else if(node.parent.leftChild == node){ 14 node.parent.leftChild = rightChild; 15 } 16 rightChild.leftChild = node; 17 node.parent = rightChild; 18 19 } 20 return null; 21 }
Up to now, after breaking the balance, a series of operations have been carried out to achieve the balance. From the above, it can be seen that there are roughly four operations as follows.
1. Balance can be achieved by only one right-handed turn.
2. Balance can be achieved by only one left-handed turn.
3. Balance can be achieved by going through left-handed and right-handed first.
4. Balance can be achieved by right-handed and left-handed first.
That's the question. How do you decide what kind of operation a broken balance will go through to achieve it?
After understanding, these four cases can be roughly divided into two categories, as follows (the following A node is the node that breaks the balance)
In the first category, the left subtree height of A node is 2 higher than that of the right subtree, which ultimately requires a right-handed operation (possibly left-first and right-second).
In the second category, the height of the left subtree of A node is 2 lower than that of the right subtree, which ultimately needs to be left-handed (probably right-left first).
So it's easy to think that after inserting a node, we can decide whether the insertion node is in the left subtree or the right subtree of A node (because the balance binary tree before insertion) and then decide which kind of operation to use, and whether we need to go through two steps to subdivide in the large operation.
The insertion element code is as follows
1 public boolean put(int val){ 2 return putVal(root,val); 3 } 4 private boolean putVal(Node node,int val){ 5 if(node == null){// Initialize the root node 6 node = new Node(val); 7 root = node; 8 size++; 9 return true; 10 } 11 Node temp = node; 12 Node p; 13 int t; 14 /** 15 * The best nodes are obtained by doing while iteration. 16 */ 17 do{ 18 p = temp; 19 t = temp.val-val; 20 if(t > 0){ 21 temp = temp.leftChild; 22 }else if(t < 0){ 23 temp = temp.rightChild; 24 }else{ 25 temp.val = val; 26 return false; 27 } 28 }while(temp != null); 29 Node newNode = new Node(p, val); 30 if(t > 0){ 31 p.leftChild = newNode; 32 }else if(t < 0){ 33 p.rightChild = newNode; 34 } 35 rebuild(p);// A Method of Balancing Binary Trees 36 size++; 37 return true; 38 }
This part of the code, detailed analysis can see a blog, binary search tree java implementation. Continue with the rebuild method code, which uses a backtracking up from the parent of the insertion node to find the unbalanced node
1 private void rebuild(Node p){ 2 while(p != null){ 3 if(calcNodeBalanceValue(p) == 2){// This indicates that the height of the left subtree needs to be right-handed or left-handed first and then right-handed. 4 fixAfterInsertion(p,LEFT);// Adjustment operation 5 }else if(calcNodeBalanceValue(p) == -2){ 6 fixAfterInsertion(p,RIGHT); 7 } 8 p = p.parent; 9 } 10 }
The calcNode BalanceValue method is the method of calculating the difference between the left and right subtree heights of the parameter. The fixAfterInsertion method is a different method of adjusting according to different types. The code is as follows
1 private int calcNodeBalanceValue(Node node){ 2 if(node != null){ 3 return getHeightByNode(node); 4 } 5 return 0; 6 } 7 // Calculation node Height of nodes 8 public int getChildDepth(Node node){ 9 if(node == null){ 10 return 0; 11 } 12 return 1+Math.max(getChildDepth(node.leftChild),getChildDepth(node.rightChild)); 13 } 14 public int getHeightByNode(Node node){ 15 if(node == null){ 16 return 0; 17 } 18 return getChildDepth(node.leftChild)-getChildDepth(node.rightChild); 19 }
1 /** 2 * Adjustment of tree structure 3 * @param p 4 * @param type 5 */ 6 private void fixAfterInsertion(Node p, int type) { 7 // TODO Auto-generated method stub 8 if(type == LEFT){ 9 final Node leftChild = p.leftChild; 10 if(leftChild.leftChild != null){//Dextral rotation 11 rightRotation(p); 12 }else if(leftChild.rightChild != null){// First left-handed and then right-handed 13 leftRotation(leftChild); 14 rightRotation(p); 15 } 16 }else{ 17 final Node rightChild = p.rightChild; 18 if(rightChild.rightChild != null){// Levo 19 leftRotation(p); 20 }else if(rightChild.leftChild != null){// First right-handed, then left-handed 21 rightRotation(p); 22 leftRotation(rightChild); 23 } 24 } 25 }
For each big class, I use the judgment of whether the left and right subtrees are empty to decide whether it is single-spin or double-spin. The reason I think is: if the code is executed in this way, then the balance must be broken. For the first big class, the left subtree height of A is 2 higher than the right subtree, which means that the balance is broken. Then I will combine the above analysis. In the first case, when an element is inserted, the tree structure is the following structure, which must be single-spin.
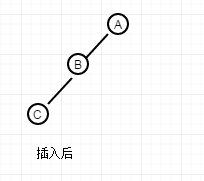
If it is the following structure, it must be this structure, from the above analysis, this structure must be double-spin.
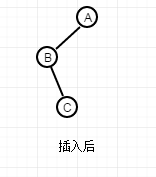
Except for these two cases, there is no other rotation. So, I'm here to decide whether the insertion node is single-spin or double-spin based on the left and right side of B node. (Here, we can't guarantee the conclusion is correct, if there are errors, we hope you can correct it.)
The above is the insertion operation of balanced binary tree and the subsequent adjustment operation code.
IV. Delete
Let's start with the deletion code of the last binary tree. For the specific deletion logic, please check the previous blog. Here we only discuss the readjustment operation.
1 p); 2 }else if(rightChild.leftChild != null){// First right-handed, then left-handed 3 rightRotation(p); 4 leftRotation(rightChild); 5 } 6 } 7 } 8 private int calcNodeBalanceValue(Node node){ 9 if(node != null){ 10 return getHeightByNode(node); 11 } 12 return 0; 13 } 14 public void print(){ 15 print(this.root); 16 } 17 public Node getNode(int val){ 18 Node temp = root; 19 int t; 20 do{ 21 t = temp.val-val; 22 if(t > 0){ 23 temp = temp.leftChild; 24 }else if(t < 0){ 25 temp = temp.rightChild; 26 }else{ 27 return temp; 28 } 29 }while(temp != null); 30 return null; 31 } 32 public boolean delete(int val){ 33 Node node = getNode(val); 34 if(node == null){ 35 return false; 36 } 37 boolean flag = false; 38 Node p = null; 39 Node parent = node.parent; 40 Node leftChild = node.leftChild; 41 Node rightChild = node.rightChild; 42 //If all parent nodes are empty, the deleted node is the root node. 43 if(leftChild == null && rightChild == null){//No child nodes 44 if(parent != null){ 45 if(parent.leftChild == node){ 46 parent.leftChild = null; 47 }else if(parent.rightChild == node){ 48 parent.rightChild = null; 49 } 50 }else{//If there is no parent node, the deleted node is the root node. 51 root = null; 52 } 53 p = parent; 54 node = null; 55 flag = true; 56 }else if(leftChild == null && rightChild != null){// Only right node 57 if(parent != null && parent.val > val){// There are parent nodes, and node The left side of the parent node 58 parent.leftChild = rightChild; 59 }else if(parent != null && parent.val < val){// There are parent nodes, and node The right side of the parent node 60 parent.rightChild = rightChild; 61 }else{ 62 root = rightChild; 63 } 64 p = parent; 65 node = null; 66 flag = true; 67 }else if(leftChild != null && rightChild == null){// Only the left node 68 if(parent != null && parent.val > val){// There are parent nodes, and node The left side of the parent node 69 parent.leftChild = leftChild; 70 }else if(parent != null && parent.val < val){// There are parent nodes, and node The right side of the parent node 71 parent.rightChild = leftChild; 72 }else{ 73 root = leftChild; 74 } 75 p = parent; 76 flag = true; 77 }else if(leftChild != null && rightChild != null){// Both sub-nodes exist 78 Node successor = getSuccessor(node);// In this case, there must be a successor node 79 int temp = successor.val; 80 boolean delete = delete(temp); 81 if(delete){ 82 node.val = temp; 83 } 84 p = successor; 85 successor = null; 86 flag = true; 87 } 88 if(flag){ 89 rebuild(p); 90 } 91 return flag; 92 } 93 94 /** 95 * Find successor nodes of node nodes 96 * 1,First determine whether the node has a right subtree, and if so, find the successor node from the left subtree of the right node, and then proceed to the next step if not. 97 * 2,Find the parent node of the node. If the right node of the parent node equals the node, continue to find the parent node. 98 * Until the parent node is Null or the right node that is not equal to the node is found. 99 * The reason is that the successor node must be larger than the node. If there is a right subtree, the successor node must exist in the right subtree. This is the reason for the first step. 100 * If there is no right subtree, there may also be a right subtree of a grandfather node of the node (that is, the parent node of the node, or a higher parent node). 101 * Iterative lookup of the node returns the node if it has one, and null if it does not. 102 * @param node 103 * @return 104 */ 105 private Node getSuccessor(Node node){ 106 if(node.rightChild != null){ 107 Node rightChild = node.rightChild; 108 while(rightChild.leftChild != null){ 109 rightChild = rightChild.leftChild; 110 } 111 return rightChild; 112 } 113 Node parent = node.parent; 114 while(parent != null && (node == parent.rightChild)){ 115 node = parent; 116 parent = parent.parent; 117 } 118 return parent; 119 }
The adjustment balance code of insertion operation is also used here. Not too much analysis
Five, traversal
Two traversals are used here, one is to traverse print data in middle order, and the other is to traverse hierarchically in order to check whether the adjusted data is correct or not.
Sequential traversal
1 public void print(){ 2 print(this.root); 3 } 4 private void print(Node node){ 5 if(node != null){ 6 print(node.leftChild); 7 System.out.println(node.val+","); 8 print(node.rightChild); 9 } 10 }
level traversal
1 /** 2 * level traversal 3 */ 4 public void printLeft(){ 5 if(this.root == null){ 6 return; 7 } 8 Queue<Node> queue = new LinkedList<>(); 9 Node temp = null; 10 queue.add(root); 11 while(!queue.isEmpty()){ 12 temp = queue.poll(); 13 System.out.print("Node value:"+temp.val+",Equilibrium value:"+calcNodeBalanceValue(temp)+"\n"); 14 if(temp.leftChild != null){ 15 queue.add(temp.leftChild); 16 } 17 if(temp.rightChild != null){ 18 queue.add(temp.rightChild); 19 } 20 } 21 }
Six, test
The test code is as follows
1 @Test 2 public void test_balanceTree(){ 3 BalanceBinaryTree bbt = new BalanceBinaryTree(); 4 bbt.put(10); 5 bbt.put(9); 6 bbt.put(11); 7 bbt.put(7); 8 bbt.put(12); 9 bbt.put(8); 10 bbt.put(38); 11 bbt.put(24); 12 bbt.put(17); 13 bbt.put(4); 14 bbt.put(3); 15 System.out.println("----Hierarchical traversal before deletion-----"); 16 bbt.printLeft(); 17 System.out.println("------Sequential traversal---------"); 18 bbt.print(); 19 System.out.println(); 20 bbt.delete(9); 21 System.out.println("----Deleted hierarchical traversal-----"); 22 bbt.printLeft(); 23 System.out.println("------Sequential traversal---------"); 24 bbt.print(); 25 }
Operation results
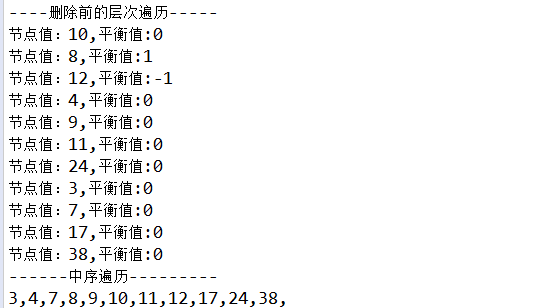
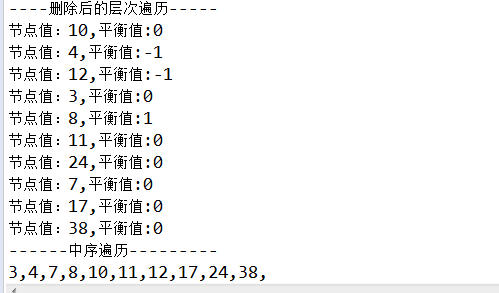
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Above is my understanding of balanced binary tree. If there are any shortcomings or errors, I hope to correct them. Thank you.