Zero. Learning objectives of this lecture

1. Understand the meaning of bit operation
2. Master the use of bit operation

1, Bit operator concept

• Bit operators are symbols that operate on each bit of binary numbers. They operate specifically on numbers 0 and 1.

2, Bitwise operator usage

(1) Classification description table

operator	operation	example	result
&	Bitwise AND	a & b	The result of "and" operation for each bit of a and b
|	Bitwise OR	a | b	The result of "or" operation for each bit of a and b
~	Reverse	~ a	The result of "not" operation for each bit of a
^	Bitwise XOR	a ^ b	The result of "XOR" operation for each bit of a and b
<<	Shift left	a << b	Move a to the left by b, and fill the space on the right with 0
>>	Shift right	a >> b	Move a right to bit b, discard the moved out bit, and fill the highest bit on the left with 0 or 1
>>>	unsigned right shift	a >>> b	Move a right to bit b, discard the moved out bit, and fill the highest bit on the left with 0

• Bitwise and operation truth table

&	0	1
0	0	0
1	0	1

• By true or table value

|	0	1
0	0	1
1	1	1

• Bitwise XOR truth table

^	0	1
0	0	1
1	1	0

• Truth table of inverse operation

~	0	1
	1	0

(2) Precautions

The essence of bit operators is to operate on binary numbers 0 and 1. When using bit operators, the operands will be converted into binary numbers for bit operation, and then the results will be converted into the desired binary numbers. Where 1 means true and 0 means false.

(3) Case demonstration

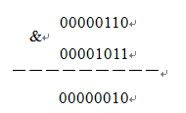
1. Bitwise AND

2. Bitwise OR

3. Bit by bit inversion

4. Bitwise XOR

5. Shift left

6. Shift right

7. Unsigned right shift

8. Demonstrate various bit operations

package net.hw.lesson05;

/**
 * Function: demonstrate bit operation
 * Author: Wei Hua
 * Date: March 22, 2020
 */
public class Example509 {
    public static void main(String[] args) {
        int a = 0b00000110;
        int b = 0b00001011;
        // Bitwise AND
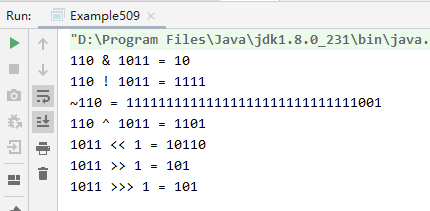
        System.out.println(Integer.toBinaryString(a) + " & " + Integer.toBinaryString(b) + " = " + Integer.toBinaryString(a & b));
        // Bitwise OR
        System.out.println(Integer.toBinaryString(a) + " ! " + Integer.toBinaryString(b) + " = " + Integer.toBinaryString(a | b));
        // Bit by bit inversion
        System.out.println("~" + Integer.toBinaryString(a) + " = " + Integer.toBinaryString(~a));
        // Bitwise XOR
        System.out.println(Integer.toBinaryString(a) + " ^ " + Integer.toBinaryString(b) + " = " + Integer.toBinaryString(a ^ b));
        // Shift left
        System.out.println(Integer.toBinaryString(b) + " << 1 = " + Integer.toBinaryString(b << 1));
        // Shift right
        System.out.println(Integer.toBinaryString(b) + " >> 1 = " + Integer.toBinaryString(b >> 1));
        // unsigned right shift 
        System.out.println(Integer.toBinaryString(b) + " >>> 1 = " + Integer.toBinaryString(b >>> 1));
    }
}

• Run the program and view the results
  

9. Demonstrate the difference between shift right and unsigned right

How can we reflect the difference between right shift and unsigned right shift?

package net.hw.lesson05;

/**
 * Function: demonstrate the difference between right shift and unsigned right shift
 * Author: Wei Hua
 * Date: March 22, 2020
 */
public class Example510 {
    public static void main(String[] args) {
        int a = 0b00000111111111111111111111111001;  // Positive number
        int b = 0b10000111111111111111111111111001;  // negative

        // Shift right
        System.out.println(Integer.toBinaryString(a) + " >> 1 = " + Integer.toBinaryString(a >> 1));
        // unsigned right shift 
        System.out.println(Integer.toBinaryString(a) + " >>> 1 = " + Integer.toBinaryString(a >>> 1));
        // Shift right
        System.out.println(Integer.toBinaryString(b) + " >> 1 = " + Integer.toBinaryString(b >> 1));
        // unsigned right shift 
        System.out.println(Integer.toBinaryString(b) + " >>> 1 = " + Integer.toBinaryString(b >>> 1));
    }
}

Run the program and the results are as follows:

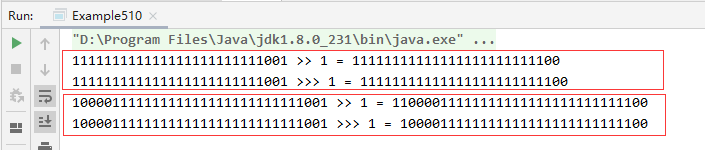
The highest bit is the sign bit, 0 is a positive number and 1 is a negative number.
For positive numbers, a right shift results in the same way as an unsigned right shift.
For negative numbers, the result of shift right is different from that of unsigned right.

(4) Classroom practice

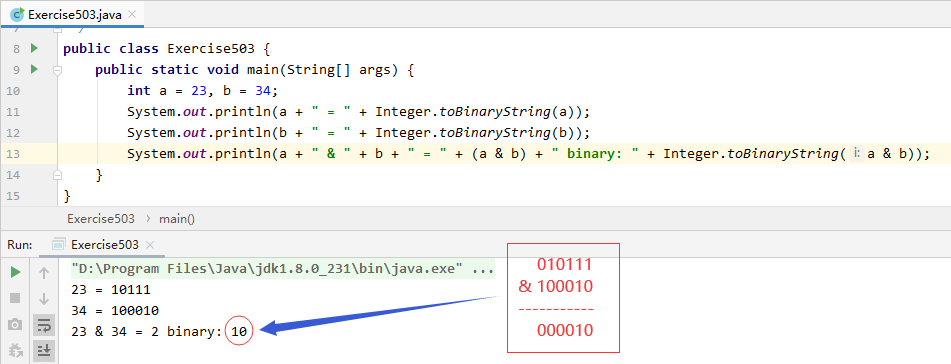
• Program and calculate the following bit operation results

1,23 & 34
2,23 | 34
3,23 ^ 34
4,~23
5,32 >> 2
6,-32 >> 2
7,32 >>> 2
8,-32 >>> 2
9,4 << 3

You can compare the bit operation of Python:

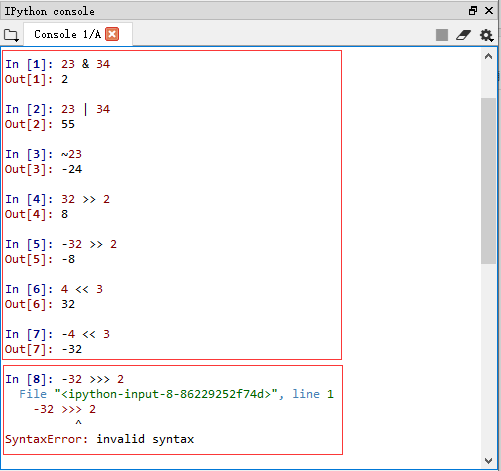
As you can see, except that there is no unsigned right shift operator in Python, other bit operators are exactly the same as Java.