Java priority queue
Introduction to PriorityQueue
PriorityQueue is the priority queue. Priority queue can ensure that the elements taken out each time are the smallest or largest elements in the queue (Java priority queue defaults to the smallest element taken out each time).
Size relationship: the comparison of elements can be naturally sorted by the element itself or passed into the comparator through the construction method.
Inheritance relationship

Through the inheritance diagram, we can know that PriorityQueue is an implementation class of the Queen interface, and the Queen interface is an implementation class of the Collection interface. Therefore, it has the basic operations of the Collection interface. In addition, the queue also provides other operations of inserting, removing and querying. Each method has two forms: one is to throw an exception (when the operation fails), and the other is to return a special value (null or false, depending on the operation).

The time complexity of peek and element operations of PriorityQueue is constant, and the time complexity of add, offer, remove and poll is log(n).
PriorityQueue example
import java.util.PriorityQueue;
public class PriorityQueueTest01 {
public static void main(String[] args) {
PriorityQueue<Integer> queue = new PriorityQueue<>();
queue.add(11);
queue.add(33);
queue.add(22);
queue.add(55);
queue.add(44);
System.out.println(queue.remove());
System.out.println(queue.remove());
System.out.println(queue.remove());
System.out.println(queue.remove());
System.out.println(queue.remove());
}
}
Operation results:
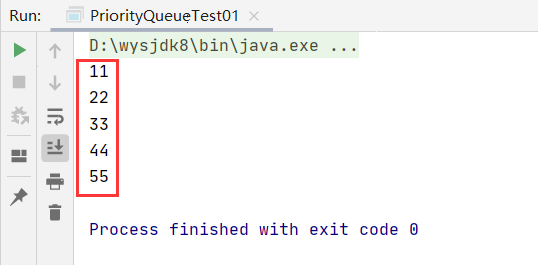
In the code, we add 11, 33, 22, 55 and 44 data in turn, and then delete them. Through the results, we find that the smallest element in the queue is deleted each time, which reflects the priority queue.
Conclusion: by default, the priority queue acquires the smallest element in the queue every time. You can also customize whether each acquisition is the smallest or the largest through the comparator.
Note: null cannot be stored in the priority queue.
Comparable comparator
Comparable interface
public interface Comparable<T> {
public int compareTo(T o);
}
There is only one public int compareTo(T o) in this interface; Method, which means to compare the object and O object. There are three return values:
1: Indicates that the current object is larger than the o object
0: indicates that the current object is equal to o object
-1: Indicates that the current object is smaller than o object
Objects stored in priority queues or collections with comparative characteristics need to implement the Comparable interface.
Requirements: store the object students in the priority queue. Each student has three attributes: id, name and age, and make the priority queue take out from small to large according to the student's id each time.
Code example:
Student class: the current class implements the Comparable interface, that is, the current class provides the default comparison method.
public class Student implements Comparable{
private int id;
private String name;
private int age;
public Student(int id, String name, int age) {
this.id = id;
this.name = name;
this.age = age;
}
public int getId() {
return id;
}
@Override
public String toString() {
return "Student{" +
"id=" + id +
", name='" + name + '\'' +
", age=" + age +
'}';
}
@Override
public int compareTo(Object o) {
Student o1 = (Student)o;
return this.id - o1.id;
}
}
PriorityQueueTest class:
public class PriorityQueueTest {
public static void main(String[] args) {
PriorityQueue<Student> queue = new PriorityQueue<>();
queue.add(new Student(2,"Wang Zhaojun",18));
queue.add(new Student(1,"Lv Bu",19));
queue.add(new Student(5,"army officer's hat ornaments",17));
queue.add(new Student(3,"Zhao Yun",20));
queue.add(new Student(4,"Jing Ke",18));
System.out.println(queue.remove());
System.out.println(queue.remove());
System.out.println(queue.remove());
System.out.println(queue.remove());
System.out.println(queue.remove());
}
}
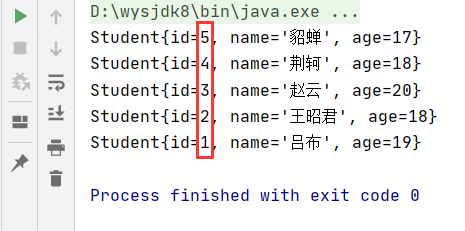
Operation results:

Comparator comparator
New requirements: what if the priority queue is taken out from large to small according to the Student ID? We will soon think of modifying the compareTo method of the Student class to make return O1 id - this. id;, In this way, we can certainly realize our new needs. However, there are many times when the compareTo method of a class cannot be modified. For example, the source code provided by JDK can only use the Comparator comparator to realize the requirements without modifying the compareTo method.
Comparator interface
public interface Comparator<T> {
int compare(T o1, T o2);
}
The interface provides the int compare(T o1, T o2) method, which requires two objects to be compared
The returned result is of type int
1: Indicates that the o1 object is larger than the o2 object
0: indicates that the o1 object is equal to the o2 object
-1: Table name o1 object is smaller than o2 object
Modify PriorityQueueTest class:
import java.util.PriorityQueue;
public class PriorityQueueTest {
public static void main(String[] args) {
PriorityQueue<Student> queue = new PriorityQueue<>(new Comparator<Student>() {
@Override
public int compare(Student o1, Student o2) {
return o2.getId() - o1.getId();
}
});
queue.add(new Student(2,"Wang Zhaojun",18));
queue.add(new Student(1,"Lv Bu",19));
queue.add(new Student(5,"army officer's hat ornaments",17));
queue.add(new Student(3,"Zhao Yun",20));
queue.add(new Student(4,"Jing Ke",18));
System.out.println(queue.remove());
System.out.println(queue.remove());
System.out.println(queue.remove());
System.out.println(queue.remove());
System.out.println(queue.remove());
}
}
Operation results:
Underlying principle
How does the priority queue ensure that the smallest (largest) element in the queue is retrieved each time? Check the source code. The underlying storage structure is an array
transient Object[] queue;
On the surface, it is an array structure. In fact, the priority queue is stored in the form of heap. By adjusting the small root heap or large root heap, it can ensure that the elements taken out each time are the smallest or largest in the queue.
Small root heap (the weight of any non leaf node is not greater than the weight of its left and right child nodes)
Large root heap (the weight of any non leaf node is greater than that of its left and right child nodes)
The underlying implementation of priority queue can be realized through array, as shown in the figure below:

The implementation of heap is based on array. The actual storage space is array. The access to data is traversed according to binary tree. The parent node and child node numbers are related, and the parent node and child node have the following relationship:
leftNo = parentNo * 2 + 1;
rightNo= parantNo * 2 + 2;
parentNo = (nodeNo - 1) / 2;
Through the above three formulas, you can easily calculate the subscripts of the parent node and child nodes of a node, which is why arrays can be used to store the heap.
Taking the small root heap as an example, how to adjust the data:
insert data
Illustration:
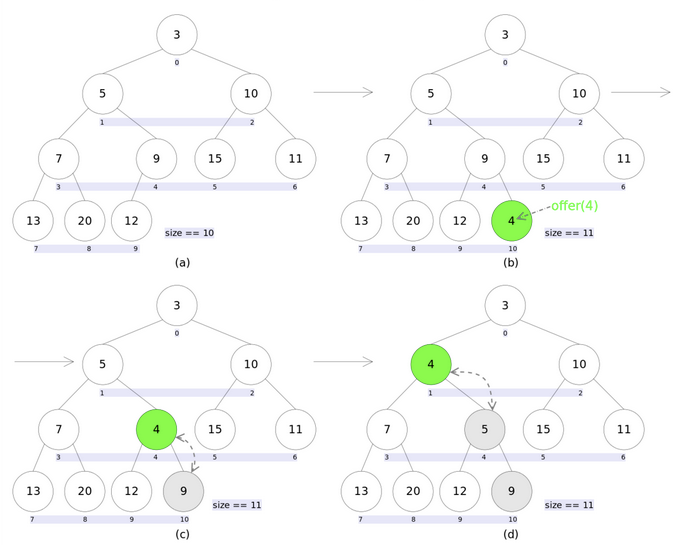
Insert data first at the last position of valid data, that is, on a leaf node. Take this node as the node to be adjusted. Compared with its parent node, if the current node is larger than the parent node and conforms to the small root heap, it does not need to be adjusted. Otherwise, it needs to be adjusted. When it is adjusted to root node 0 or one of its positions, the current node will terminate when it is larger than the parent node.
The source code is as follows:
//The bottom-up adjustment process k represents the position of the element to be inserted, and x represents the data to be inserted
private void siftUpUsingComparator(int k, E x) {
while (k > 0) {
//Find the parent node through the current node k to be adjusted
int parent = (k - 1) >>> 1;
Object e = queue[parent];
//If the parent node data is smaller than the node data to be inserted at this time, meet the small root heap, and break exits
if (comparator.compare(x, (E) e) >= 0)
break;
//If the small root heap is not satisfied, insert the parent node value into the node to be inserted
queue[k] = e;
//The position to be compared points to the parent node
k = parent;
}
queue[k] = x;
}
Delete data
Illustration:
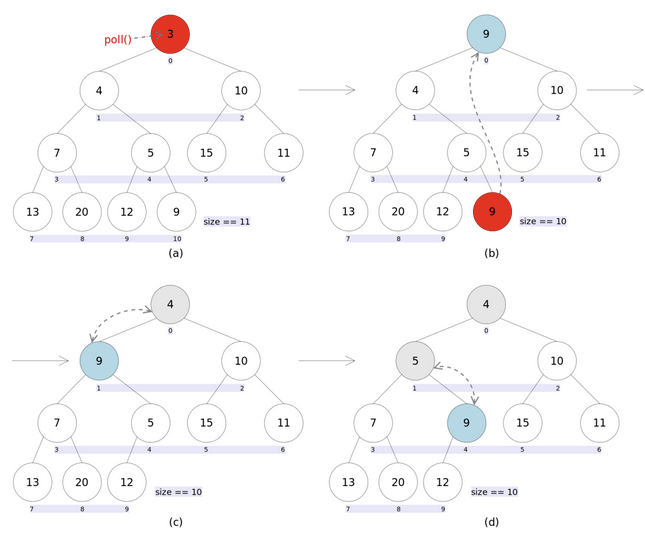
Because it is a small root heap and its top element is the smallest, the elements deleted are the top elements. In the process of deleting the top element of the heap, first record the position of subscript 0 and replace the element of subscript 0 with the last element. The current small root heap may be damaged. It is necessary to adjust the heap. Starting from the position specified by k, it will be exchanged with the smaller of the current left and right children layer by layer until x is less than or equal to any one of the left and right children.
The source code is as follows:
//Delete the node, adjust the position to be compared from top to bottom, and adjust the element x to be adjusted
private void siftDownUsingComparator(int k, E x) {
//To adjust size/2 from top to bottom, just compare it to size/2,
//Because size/2 has reached the leaf node, there is no need to adjust it.
int half = size >>> 1;
while (k < half) {
//Find the left child of the current node
int child = (k << 1) + 1;
Object c = queue[child];
int right = child + 1;//Right child node subscript
//Find the smallest node of the left and right children, record the position in child, and record the value in c
if (right < size && comparator.compare((E) c, (E) queue[right]) > 0)
c = queue[child = right];
//When the minimum value of the left and right children is greater than the x value of the parent node and meets the small root heap, the adjustment process is ended
if (comparator.compare(x, (E) c) <= 0)
break;
//The smallest child node is smaller than the parent node, which does not meet the small root heap and needs to be adjusted
queue[k] = c;
k = child;
}
queue[k] = x;
}