Search tree

Binary search tree, also known as binary sort tree, is either an empty tree * * or a binary tree with the following properties:

• If its left subtree is not empty, the values of all nodes on the left subtree are less than those of the root node
• If its right subtree is not empty, the values of all nodes on the right subtree are greater than those of the root node
• Its left and right subtrees are also binary search trees

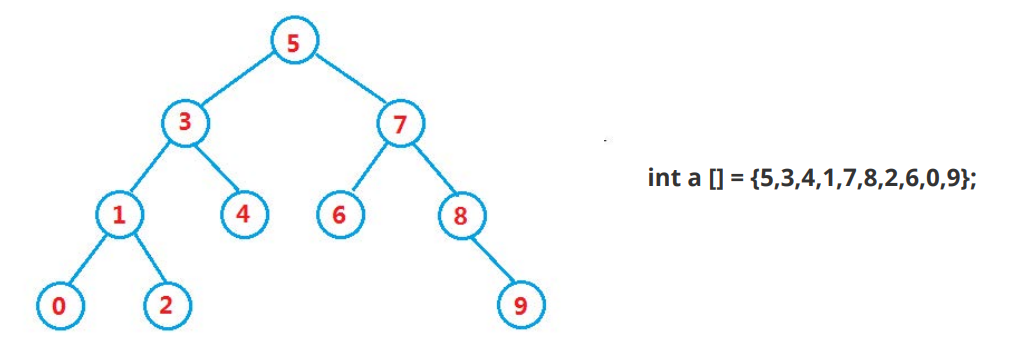
Operations: find, insert, delete

Logic code:

class BinarySearchTree {
    static class BSNode {
        public int val;
        public BSNode left;
        public BSNode right;

        public BSNode(int val) {
            this.val = val;
        }
    }
    public BSNode root = null;

    /*
    lookup
     */
    public BSNode search(int val) {
        if(root == null) return null;
        BSNode cur = root;
        while (cur != null) {
            if(cur.val == val) {
                return cur;
            }else if(cur.val < val) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }

    /*
    insert
     */
    public boolean insert(int val) {
        BSNode bsNode = new BSNode(val);
        if(root == null) {
            root = bsNode;
            return true;
        }
        BSNode cur = root;
        BSNode parent = null;

        while (cur != null) {
            if(cur.val == val) {
                return false;
            }else if(cur.val < val) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        if(parent.val < val) {
            parent.right = bsNode;
        }else {
            parent.left = bsNode;
        }
        return true;
    }

    /*
    delete
     */
    public void remove(int val) {
        if (root == null) return;
        BSNode cur = root;
        BSNode parent = null;
        while (cur != null) {
            if (cur.val == val) {
                removeNode(parent,cur,val);
                return;
            } else if (cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else {
                parent = cur;
                cur = cur.left;
            }
        }
    }

    public void removeNode(BSNode parent, BSNode cur, int val) {
        if (cur.left == null) {
            if (root == cur) {
                root = cur.right;
            } else if (parent.left == cur) {
                parent.left = cur.right;
            } else {
               parent.right = cur.right;
            }
        } else if (cur.right == null) {
            if (root == cur) {
                root = cur.left;
            } else if (parent.left == cur) {
                parent.left = cur.left;
            } else {
                parent.right = cur.left;
            }
        } else {
            BSNode targetParent =cur;
            BSNode target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if (target == targetParent.left) {
                targetParent.left = target.right;
            } else {
                targetParent.right = target.right;
            }

        }
    }
}

Find logic:

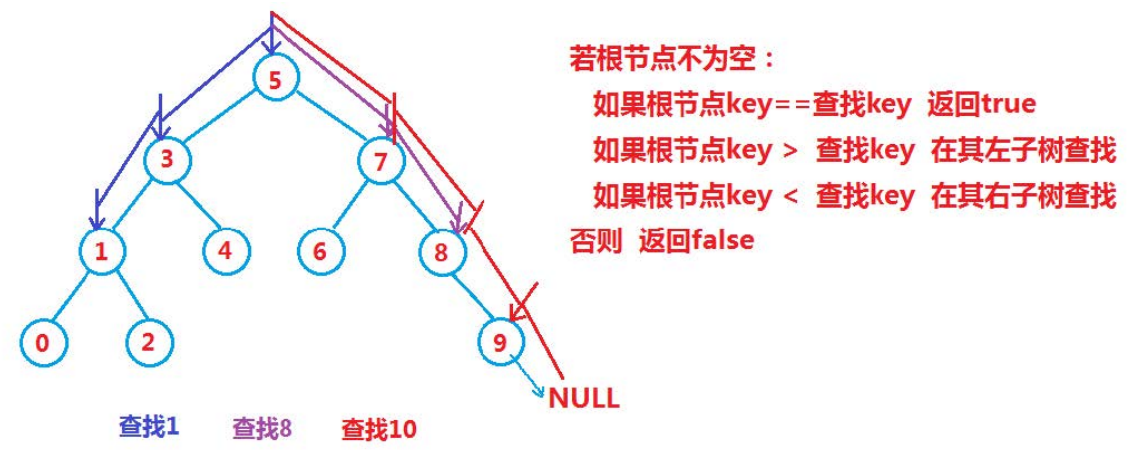
Insert logic:

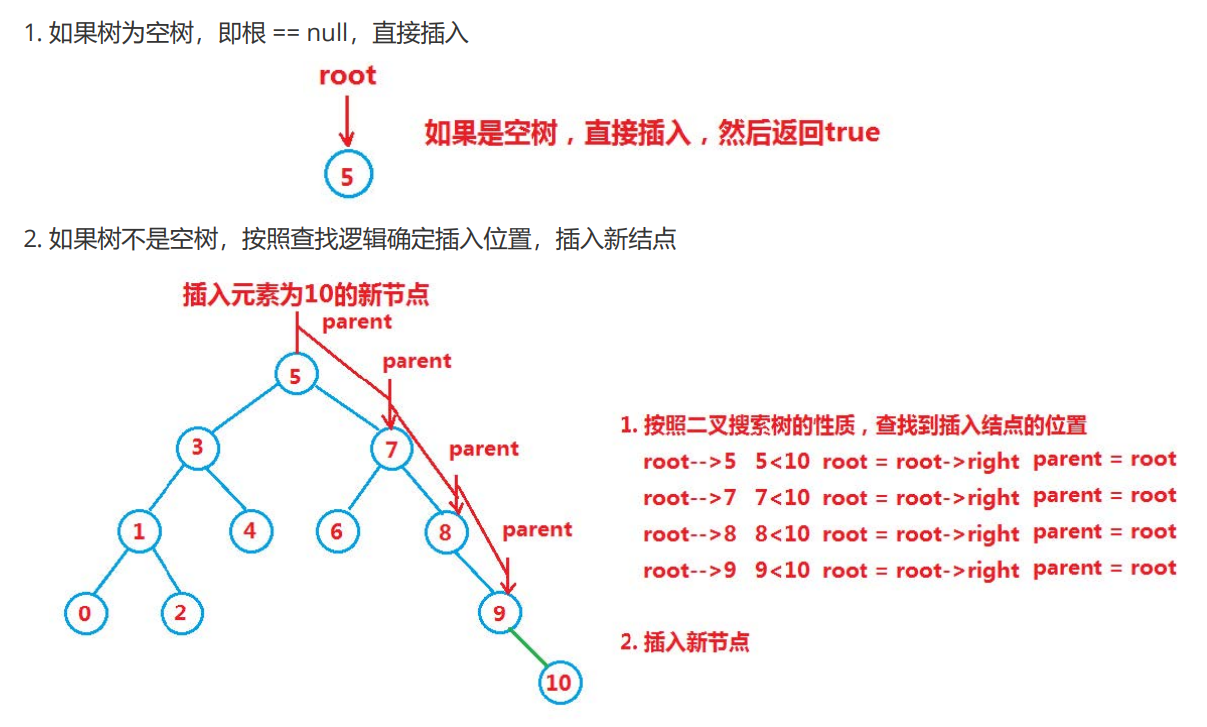
Delete logic: set the node to be deleted as cur and the parent node of the node to be deleted as parent

1. cur.left == null if cur is root, then root = cur Right if cur is not root, cur is parent Left, then parent left = cur. Right if cur is not root, cur is parent Right, then parent right = cur. right
2. cur.right == null if cur is root, then root = cur Left if cur is not root, cur is parent Left, then parent left = cur. Left if cur is not root, cur is parent Right, then parent right = cur. left
3. cur. left != null && cur. right != Null needs to be deleted by using the replacement method, that is, find the first node in the middle order in its right subtree (with the smallest key), fill its value into the deleted node, and then deal with the deletion of the node.

Test code:

public class TestDemo {
    public static void preOrder(BinarySearchTree.BSNode root) {
        if(root == null) {
            return;
        }
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

    public static void inOrder(BinarySearchTree.BSNode root) {
        if(root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }

    public static void main(String[] args) {
        BinarySearchTree binarySearchTree = new BinarySearchTree();
        binarySearchTree.insert(6);
        binarySearchTree.insert(4);
        binarySearchTree.insert(3);
        binarySearchTree.insert(1);
        binarySearchTree.insert(9);
        binarySearchTree.insert(15);
        binarySearchTree.insert(8);
        binarySearchTree.insert(11);
        preOrder(binarySearchTree.root);
        System.out.println();
        inOrder(binarySearchTree.root);
        System.out.println();
        //Find node 5
        try {
            BinarySearchTree.BSNode ret = binarySearchTree.search(6);
            System.out.println("The node was found:" + ret.val);
        }catch (NullPointerException e) {
            System.out.println("The node was not found~");
        }
        //Find node 14
        try {
            BinarySearchTree.BSNode ret = binarySearchTree.search(14);
            System.out.println(ret.val);
        }catch (NullPointerException e) {
            System.out.println("The current node was not found~");
        }
        System.out.println("======Delete 15 nodes======");
        binarySearchTree.remove(15);
        preOrder(binarySearchTree.root);
        System.out.println();
        inOrder(binarySearchTree.root);
        System.out.println();
        System.out.println("======Delete 6 nodes======");
        binarySearchTree.remove(6);
        preOrder(binarySearchTree.root);
        System.out.println();
        inOrder(binarySearchTree.root);
        System.out.println();
    }
}

The running result of this code is:

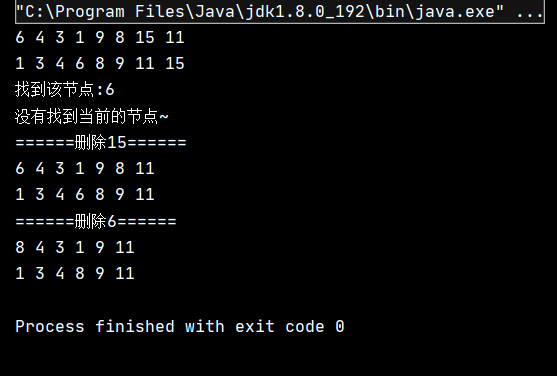
performance analysis

Both insert and delete operations must be searched first. The search efficiency represents the performance of each operation in the binary search tree.

For a binary search tree with n nodes, if the search probability of each element is equal, the average search length of the binary search tree is a function of the depth of the node in the binary search tree, that is, the deeper the node, the more comparisons.

However, for the same key set, if the insertion order of each key is different, binary search trees with different structures may be obtained:

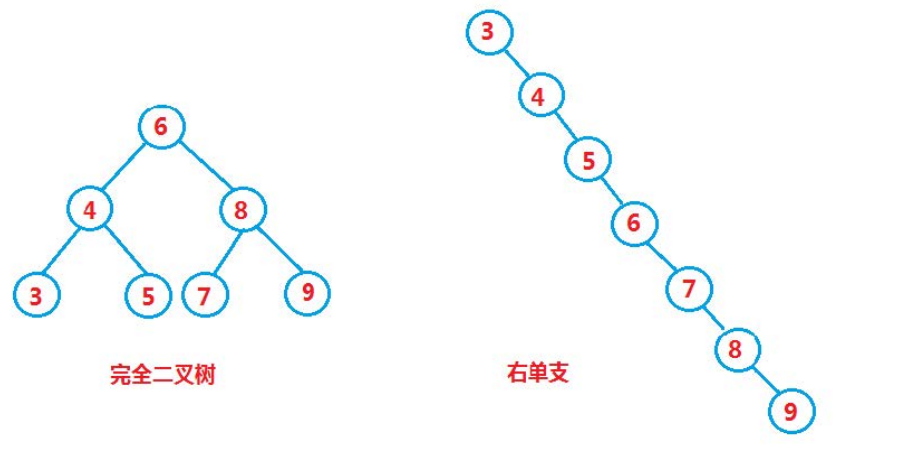
In the optimal case, the binary search tree is a complete binary tree, and its time complexity is O(logN)
In the worst case, the binary search tree degenerates into a single branch tree, and its time complexity is O(N)

search

Map and set are special containers or data structures for searching, and their search efficiency is related to their specific instantiation subclasses.

Search methods are:

1. Direct traversal. The time complexity is O(N). If there are many elements, the efficiency will be very slow
2. Binary search, the time complexity is O(logN), but the sequence must be ordered before search

The above sorting is more suitable for static type search, that is, the interval is generally not inserted or deleted, but in reality, such as:

1. Query test scores by name
2. Address book, that is, to query the contact information according to the name
3. Do not duplicate the collection, that is, you need to search whether the keyword is already in the collection

Some insertion and deletion operations, i.e. dynamic search, may be performed during search, so the above two methods are not suitable. Map and Set are collection containers suitable for dynamic search.

Model

Generally, the data searched is called a Key, the data corresponding to the Key is called a Value, and it is called a Key Value pair

There are two models:

1. Pure key model, such as:

• There is an English dictionary to quickly find out whether a word is in the dictionary.
• Quickly find out if a name is in the address book.

1. Key value model, such as:

• Count the number of occurrences of each word in the file. The statistical resu lt is that each word has its corresponding number of occurrences: < word, number of occurrences of word >.
• Liangshan hero's Jianghu nickname: every hero has his own Jianghu nickname.

The Key value pair of Key value is stored in the Map, and only Key is stored in the Set.

Use of Map

Description of Map

Map is an interface class, which does not inherit from Collection. The key value pairs of < K, V > structure are stored in this class, and K must be unique and cannot be repeated.

About map Description of entry < K, V >

Map. Entry < K, V > is an internal class implemented in map to store the mapping relationship between < Key, value > Key value pairs. This internal class mainly provides the acquisition of < Key, value >, the setting of value and the comparison method of keys.

method	explain
K getKey()	Return the key in the entry
V getValue()	Return value in entry
V setValue(V value)	Replace the value in the key value pair with the specified value

Note: map Entry < K, V > does not provide a method to set the Key

Description of common methods of Map

method	explain
V get(Object key)	Returns the value corresponding to the key
V getOrDefault(Object key, V defaultValue)	Return the value corresponding to the key. If the key does not exist, return the default value
V put(K key, V value)	Set the value corresponding to the key
V remove(Object key)	Delete the mapping relationship corresponding to the key
Set< K> keySet()	Returns the non duplicate collection of all key s
Collection< V > values()	Returns a repeatable set of all value s
Set<Map.Entry<K, V>> entrySet()	Returns all key value mappings
boolean containsKey(Object key)	Determine whether the key is included
boolean containsValue(Object value)	Judge whether value is included

be careful:

1. Map is an interface and cannot instantiate an object directly. If you want to instantiate an object, you can only instantiate its implementation class TreeMap or HashMap
2. The Key of the Key value pair stored in the Map is unique, and the value can be repeated
3. All keys in the Map can be separated and stored in the Set for access (because keys cannot be repeated).
4. All values in the Map can be separated and stored in any subset of the Collection (values may be duplicated).
5. The key of the key value pair in the Map cannot be modified directly, but the value can be modified. If you want to modify the key, you can only delete the key first and then insert it again.

The difference between TreeMap and HashMap

Map infrastructure	TreeMap	HashMap
Bottom structure	Red black tree	Hash bucket
Insert / delete / find time complexity	O(log2N)	O(1)
Is it orderly	About Key ordering	disorder
Thread safety	unsafe	unsafe
Insert / delete / find differences	Element comparison is required	Calculate the hash address through the hash function
Compare and overwrite	key must be able to compare, otherwise ClassCastException will be thrown	Custom types need to override the equals and hashCode methods
Application scenario	In the scenario where the Key needs to be ordered	I don't care whether the Key is orderly or not. It requires higher time performance

Use of Set

There are two main differences between Set and Map: Set is an interface class inherited from Collection, and only Key is stored in Set.

Description of common methods

method	explain
boolean add(E e)	Add elements, but duplicate elements will not be added successfully
void clear()	Empty collection
boolean contains(Object o)	Determine whether o is in the set
Iterator< E > iterator()	Return iterator
boolean remove(Object o)	Delete o from collection
int size()	Returns the number of elements in a set
boolean isEmpty()	Check whether set is empty. If it is empty, return true; otherwise, return false
Object[] toArray()	Converts elements in a set to an array and returns
boolean containsAll(Collection<?> c)	Whether all the elements in the set c exist in the set returns true; otherwise, it returns false
boolean addAll(Collection<? extends E> c)	Adding the elements in set c to set can achieve the effect of de duplication

be careful:

1. Set is an interface class inherited from Collection
2. Only the key is stored in the Set, and the key must be unique
3. The bottom layer of Set is implemented using Map, which uses a default Object of key and Object as a key value pair inserted into the Map
4. The biggest function of Set is to de duplicate the elements in the Set
5. The common classes that implement the Set interface include TreeSet and HashSet, and a LinkedHashSet. LinkedHashSet maintains a two-way linked list on the basis of HashSet to record the insertion order of elements.
6. The Key in the Set cannot be modified. If you want to modify it, first delete the original Key and then insert it again

The difference between TreeSet and HashSet

Set underlying structure	TreeSet	HashSet
Bottom structure	Red black tree	Hash bucket
Insert / delete / find time complexity	O(log2N)	O(1)
Is it orderly	About Key ordering	Not necessarily orderly
Thread safety	unsafe	unsafe
Insert / delete / find differences	Insert and delete according to the characteristics of red black tree	First calculate the key hash address, and then insert and delete it
Compare and overwrite	key must be able to compare, otherwise ClassCastException will be thrown	Custom types need to override the equals and hashCode methods
Application scenario	In the scenario where the Key needs to be ordered	I don't care whether the Key is orderly or not. It requires higher time performance

Map and Set exercises

A number that appears only once

Digital force buckle links that appear only once

class Solution {
    public int singleNumber(int[] nums) {
        HashSet<Integer> set = new HashSet<>();
        for(int i = 0;i < nums.length;i++) {
            if (set.contains(nums[i])) {
                set.remove(nums[i]);
            } else {
                set.add(nums[i]);
            }
        }
        for(int i = 0;i < nums.length;i++) {
            if (set.contains(nums[i])) {
                return nums[i];
            } 
        }
        return -1;
    }
}

Use the Set method to solve the problem.

Copy linked list with random pointer

Copy Chain Watch force buckle link with random pointer

class Solution {
    public Node copyRandomList(Node head) {
        if (head == null) return null;
        HashMap<Node,Node> map = new HashMap<>();
        Node cur = head;
        while (cur != null) {
            Node node = new Node(cur.val);
            map.put(cur,node);
            cur = cur.next;
        }
        cur = head;
        while (cur != null) {
            map.get(cur).next = map.get(cur.next);
            map.get(cur).random = map.get(cur.random);
            cur = cur.next;
        }
        return map.get(head);
    }
}

The code passed the test.

Gemstones and stones

Gem and stone clasp link

class Solution {
    public int numJewelsInStones(String jewels, String stones) {
        HashSet<Character> set = new HashSet<>();
        int count = 0;
        for(char ch:jewels.toCharArray()) {
            set.add(ch);
        }

        for(char ch:stones.toCharArray()) {
            if(set.contains(ch)) {
                count++;
            }
        }
        return count;
    }
}

The code passed the test.

Bad keyboard typing

Bad keyboard typing cattle guest link

import java.util.*;

public class Main {
    public static void function(String strExc,String strAct) {
        HashSet<Character> setAct = new HashSet<>();
        for (char ch:strAct.toUpperCase().toCharArray()) {
            setAct.add(ch);
        }
        
        HashSet<Character> setBroken = new HashSet<>();
        for (char ch:strExc.toUpperCase().toCharArray()) {
            if (!setAct.contains(ch) && !setBroken.contains(ch)) {
                setBroken.add(ch);
                System.out.print(ch);
            }
        }
    }
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String strExc = sc.nextLine();
        String strAct = sc.nextLine();
        function(strExc,strAct);
    }
}

The code passed the test.

Top K high frequency words

Top K high-frequency word force buckle links

Hashtable

concept

In order structure and balance tree, there is no corresponding relationship between element key and its storage location. Therefore, when looking for an element, you must compare the key multiple times. The time complexity of sequential search is O(N), and the height of the tree in the binary search tree is O(log2N). The search efficiency depends on the comparison times of elements in the search process.

Ideal search method: you can get the elements to be searched directly from the table at one time without any comparison. If a storage structure is constructed to establish a one-to-one mapping relationship between the storage location of an element and its key code through a function (hashFunc), the element can be found quickly during search. When adding to this structure:

• Insert element:
  According to the key of the element to be inserted, this function calculates the storage location of the element and stores it according to this location.
• Search elements:
  Carry out the same calculation for the key of the element, take the obtained function value as the storage location of the element, and compare the elements according to this location in the structure. If the key codes are equal, the search is successful.

This method is called hash (hash) method. The conversion function used in hash method is called hash (hash) function, and the structure constructed is called hash table (or Hash list).
The hash function is set to: hash(key) = key% the total size of the underlying space of the storage element.
For example: data set {1, 7, 6, 4, 5, 9};

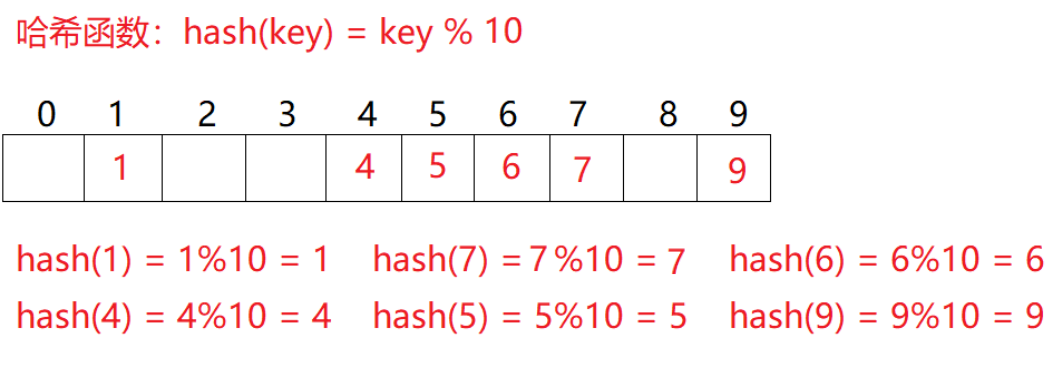
This method does not need to compare multiple key codes, so the search speed is relatively fast. Problem: according to the above hash method, inserting element 44 into the set will cause hash conflict.

Hash Collisions

Concept: for the keywords Ki and kJ (I! = J) of two data elements, there is ki= KJ, but hash (KI) = = hash (kJ), that is, different keywords calculate the same hash address through the same hash number. This phenomenon is called hash collision or hash collision.
Data elements with different keys and the same hash address are called "synonyms".

Avoidance: first of all, we need to make it clear that the capacity of the underlying array of our hash table is often less than the actual number of keywords to be stored, which leads to a problem. The occurrence of conflict is inevitable, but what we can do is to reduce the conflict rate as much as possible.

Conflict avoidance -- hash function design

One reason for hash conflict may be that the hash function design is not reasonable.

Hash function design principles

• The definition field of hash function must include all keys to be stored. If the hash table allows m addresses, its value field must be between 0 and m-1.
• The addresses calculated by the hash function can be evenly distributed in the whole space.
• Hash functions should be simple.

Common hash functions

1. Direct customization method (common)
   Take a linear function of the keyword as the Hash address: Hash (Key) = A*Key + B advantages: simple and uniform disadvantages: you need to know the distribution of keywords in advance. Usage scenario: it is suitable for finding small and continuous situations.
2. Division and residue method (common)
   Let the number of addresses allowed in the hash table be m, take a prime number p not greater than m but closest to or equal to m as the divisor, and convert the key code into a hash address according to the hash function: hash (key) = key% p (p < = m).
3. Square middle method
   Assuming that the keyword is 1234, its square is 1522756, and the middle 3 bits 227 are extracted as the hash address; For another example, if the keyword is 4321, its square is 18671041, and the middle three bits 671 (or 710) are extracted as the hash address. The square median method is more suitable: do not know the distribution of keywords, and the number of digits is not very large.
4. Folding method
   The folding method is to divide the keyword from left to right into several parts with equal digits (the digits of the last part can be shorter), then overlay and sum these parts, and take the last few digits as the hash address according to the length of the hash table.
   The folding method is suitable for the situation that there is no need to know the distribution of keywords in advance and there are many keyword digits.
5. Random number method
   Select a random function and take the random function value of the keyword as its hash address, that is, H(key) = random(key), where random is a random number function. This method is usually used when the keyword length is different
6. Mathematical analysis
   There are n d digits. Each bit may have r different symbols. The frequency of these r different symbols may not be the same in each bit. They may be evenly distributed in some bits. The opportunities of each symbol are equal. They are unevenly distributed in some bits, and only some symbols often appear. According to the size of the hash table, several bits in which various symbols are evenly distributed can be selected as the hash address. For example:
   
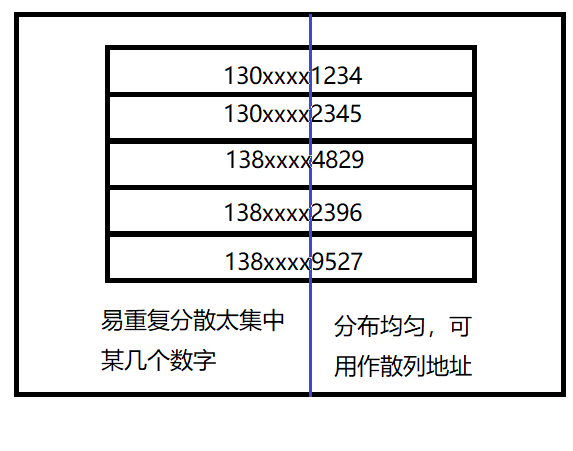
   Suppose you want to store the employee registration form of a company. If you use the mobile phone number as the keyword, it is very likely that the first seven digits are the same. Then we can select the next four digits as the hash address. If such extraction is prone to conflict, you can also reverse the extracted numbers (for example, 1234 is changed to 4321), right ring displacement (for example, 1234 is changed to 4123) Left ring shift, superposition of the first two numbers and the last two numbers (for example, 1234 is changed to 12 + 34 = 46), etc.
   Digital analysis method is usually suitable for dealing with the situation of large number of keywords, if the distribution of keywords is known in advance and several bits of keywords are evenly distributed.

Note: the more sophisticated the hash function is designed, the lower the possibility of hash conflict, but hash conflict cannot be avoided.

Conflict avoidance - load factor adjustment

Rough demonstration of the relationship between load factor and conflict rate:

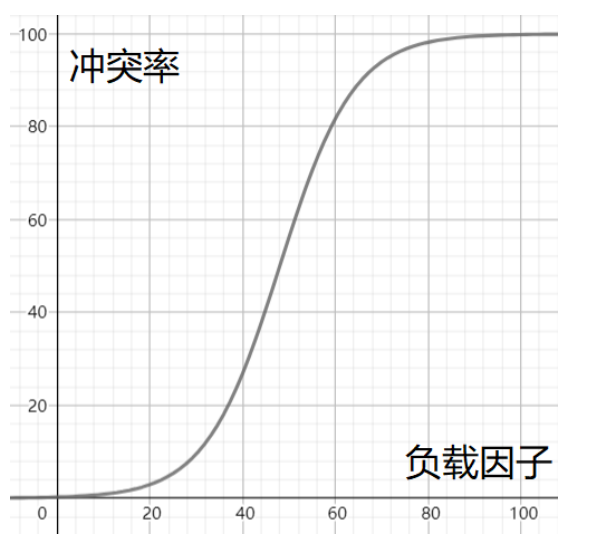
Therefore, when the conflict rate reaches an intolerable level, it is necessary to reduce the conflict rate in disguise by reducing the load factor. Given that the number of existing keywords in the hash table is immutable, only the size of the array in the hash table is adjusted.

The default load factor at the bottom of HashMap is 0.75.

conflict resolution

There are two common ways to resolve hash conflicts: closed hash and open hash.

Conflict resolution - closed hash

Closed hash: also known as open addressing method. In case of hash conflict, if the hash table is not full, it means that there must be an empty position in the hash table, then the key can be stored in the "next" empty position in the conflict position.
How to find the next empty location:

1. Linear detection:
   Start from the position where the conflict occurs and probe backward in turn until the next empty position is found.
   Insert: obtain the position of the element to be inserted in the hash table through the hash function; If there is no element in this position, a new element is directly inserted. If there is a hash conflict in this position, use linear detection to find the next empty position and insert a new element.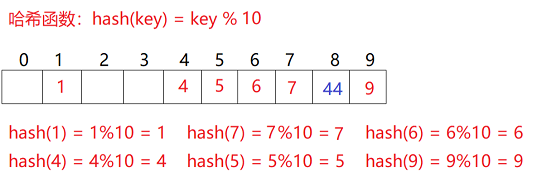
   When using closed hash to deal with hash conflicts, existing elements in the hash table cannot be deleted physically. Deleting elements directly will affect the search of other elements. For example, if element 4 is deleted directly, 44 searching may be affected. Therefore, linear detection uses the marked pseudo deletion method to delete an element.

2. Secondary detection
   The defect of linear detection is that conflicting data are stacked together, which is related to finding the next empty position. Because the way to find the empty position is to find it one by one next to each other, the secondary detection is to avoid this problem, The method to find the next empty position is: Hi = (H0 + i2)% m, or: Hi = (H0 - i2)% m, where: i = 1,2,3.... H0 is the position obtained by calculating the key key of the element through the hash function Hash(x), and M is the size of the table. If 44 is to be inserted in 2.1, there is a conflict. The situation after use is resolved as follows: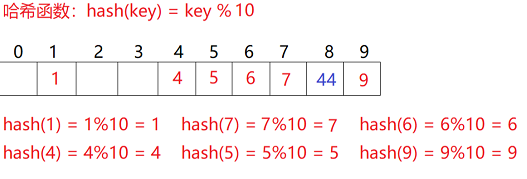
   When the length of the table is prime and the table loading factor a does not exceed 0.5, new table entries can be inserted, and any position will not be probed twice. Therefore, as long as there are half empty positions in the table, the table will not be full. When searching, you can not consider that the table is full, but you must ensure that the table loading factor a does not exceed 0.5 when inserting. If it exceeds 0.5, you must consider capacity expansion.

Therefore, the biggest defect of closed hash is the low space utilization, which is also the defect of hash.

Conflict resolution - Open hash / hash bucket

The open hash method, also known as the chain address method (open chain method), first uses the hash function to calculate the hash address for the key code set. The key codes with the same address belong to the same subset. Each subset is called a bucket. The elements in each bucket are linked through a single linked list, and the head nodes of each linked list are stored in the hash table.

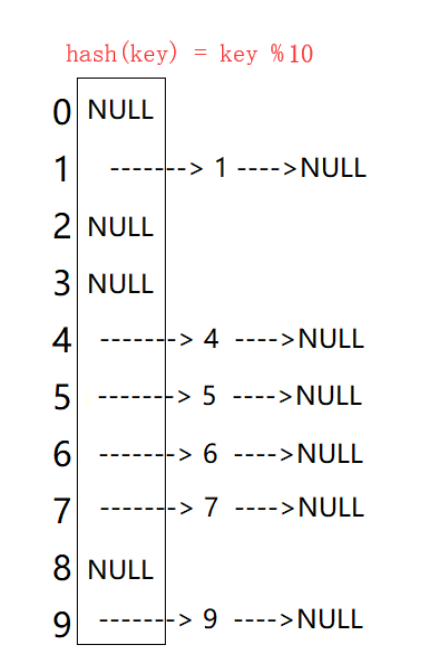
As can be seen from the above figure, each bucket in the open hash contains elements with hash conflicts.
Open hash: it can be considered that a search problem in a large set is transformed into a search in a small set.

Solutions in times of serious conflict

In fact, the hash bucket can be regarded as transforming the search problem of a large set into the search problem of a small set. If the conflict is serious, it means that the search performance of a small set is actually poor. At this time, we can continue to transform the so-called small set search problem, for example:

1. Behind each bucket is another hash table
2. Behind each bucket is a search tree

Starting from JDK 1.8, every time it is tail inserted, and when the length of the linked list exceeds 8, the linked list will be converted into a red black tree.