1. Bubble sorting

1.1 idea of fake sorting

Bubble sorting is a simple sorting algorithm. It repeatedly accesses the sequence to be sorted, compares two elements at a time, and exchanges elements if their order is different from the expected idea. The comparison operation between elements is repeated until the elements no longer need to be exchanged, and then the sorting process has been completed.

1.2 algorithm description

• Compare adjacent elements, and exchange elements if the former element is greater than the latter.
• Each comparison compares each pair of adjacent elements. After a round, the largest element will appear at the end.
• Repeat the above steps until the sorting is completed.

1.3 code implementation

 public static void bubbleSort(int[] array){
        if(array==null||array.length==0){
            return;
        }
        for(int i =0;i<array.length-1;i++){
            for(int j =0;j<array.length-1-i;j++){
                if(array[j]>array[j+1]){
                    int tmp=array[j];
                    array[j]=array[j+1];
                    array[j+1]=tmp;
                }
            }
        }
    }

The above codes are repeatedly compared, especially if the subsequent arrangement is normal, the comparison will be repeated. Therefore, in order to reduce this situation, the above codes are optimized.

public static void optimizedBubbleSort(int[] array){
        if(array==null||array.length==0){
            return;
        }
        //Set the mark. If the subsequent arrangement is normal, there is no need to continue bubbling
        boolean nextSort=true;
        for(int i=0;i<array.length-1&&nextSort;i++){
            nextSort=false;
            for (int j =0;j<array.length-1-i;j++){
                if(array[j]>array[j+1]){
                    int tmp=array[j];
                    array[j]=array[j+1];
                    array[j+1]=tmp;
                    nextSort=true;
                }
            }
        }
    }

1.4 algorithm analysis

• Time complexity analysis:
  Optimal time complexity: O(n) worst case O(n^2) average time complexity: O(n^2)
• Spatial complexity analysis: average spatial complexity: O(1)
• Stability: stable

2. Select Sorting

2.1 idea of selecting sorting

Characteristics of selective sorting: selective sorting is an unstable sorting algorithm, because no matter what data is sorted, it is O(n^2) time complexity. Because the time complexity of selective sorting is relatively large, when selective sorting is used, the smaller the data size is, the better.

2.2 algorithm description

• Find the smallest (or largest) element in the sequence to be sorted, and store the sorting sequence at the starting position.
• Continue to look for the smallest (or largest) element in the remaining sequence to be sorted, and arrange it at the end of the sorting sequence.
• Repeat the second step until the sequence sorting is completed.

2.3 code implementation

    public static void selectSort(int []array){
        if(array==null||array.length==0){
            return;
        }
        for(int i=0;i<array.length;i++){
            int minIndex=i;
            for(int j=i+1;j<array.length;j++){
                if(array[j]<array[minIndex]){
                    minIndex=j;
                }
            }
            //minIndex is the smallest subscript of the element
            if(minIndex!=i){
                int tmp=array[i];
                array[i]=array[minIndex];
                array[minIndex]=tmp;
            }
        }
    }

Optimization: in the process of finding elements each time, directly find two elements, namely, the largest element and the smallest element in the sequence to be sorted.

    public static void optimizedSelectSort(int[]array){
        if(array==null||array.length==0){
            return;
        }
        for(int i=0;i<array.length/2;i++){
            int minIndex=i;
            int maxIndex=i;
            for(int j=i+1;j<array.length-1-i;j++){
                if(array[j]<array[minIndex]){
                    minIndex=j;
                    continue;
                }
                if(array[j]>array[maxIndex]){
                    maxIndex=j;
                }
            }

            int tmp=array[i];
            array[i]=array[minIndex];
            array[minIndex]=tmp;
            //Determine whether the value of maxIndex is i
            if(maxIndex==i){
                maxIndex=minIndex;
            }
            tmp=array[maxIndex];
            array[maxIndex]=array[array.length-1-i];
            array[array.length-1-i]=tmp;
        }
    }

2.4 algorithm analysis

• Time complexity analysis:
  Optimal time complexity O(n^2) average time complexity O(n^2) worst time complexity O(n^2)
• Spatial complexity analysis: average spatial complexity: O(1)
• Stability: unstable

3. Insert sort

3.1 insert sorting idea

The insertion sorting algorithm is to build an ordered sequence. For unsorted data, search from back to front in the sorted sequence, and insert the position after finding the elements that meet the conditions.

3.2 algorithm description

• Starting from the first element, the element can be considered as a sorted element;
• Take out the next element and search from back to front among the sorted elements;
• If the sorted element is larger than the new element, move the element to the next position;
• Repeat step 3 until the sorted element is found to be less than or equal to the new element, and then insert the element.

3.3 code implementation

    public static void insertSort(int []array){
        if(array==null||array.length==0){
            return;
        }
        for(int i=0;i<array.length;i++){
            int tmp=array[i];//Get the element
            int j=i;
            while(j>0&&tmp<array[j-1]){
                array[j]=array[j-1];
                j--;
            }
            array[j]=tmp;
        }
    }

3.4 algorithm analysis

• Time complexity analysis:
• Optimal time complexity: O(n) average time complexity: O(n^2) worst time complexity: O(n^2)
• -Spatial complexity analysis: average spatial complexity: O(1)
• Stability analysis: stability

4. Heap sorting

4.1 idea of heap sorting

Heap is a complete binary tree stored sequentially. The values of all non terminal nodes in a complete binary tree are not greater than (or less than) the values of their left and right child nodes. Where the value of each node is less than or equal to the values of their left and right children, such a heap is called a small root heap; where the value of each node is greater than or equal to the values of their left and right children, such a heap is called a large root heap;
Heap sort is a sort algorithm designed by using heap data structure. Heap sorting makes use of the maximum (or minimum) key of the records at the top of the large root heap (or small root heap), which makes it easy to select the records with the maximum (or minimum) key in the current unordered area.

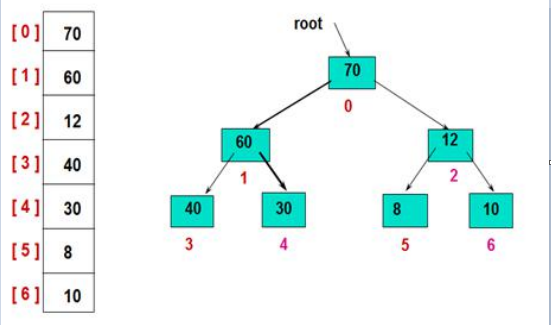
4.2 algorithm description

Basic idea of sorting with large root heap:

• First, build the initial array into a large root heap, which is the initial unordered heap
• Then, the record R[1] (i.e. the top of the heap) with the largest keyword is exchanged with the last record R[n] of the unordered area, so as to obtain a new unordered area R[1... N-1] and ordered area R[n]. Since the new root R[1] after exchange may violate the heap nature, the current unordered region R[1... N-1] should be adjusted to heap. Then, the record R[1] with the largest keyword in R[1... N-1] is exchanged with the last record R[n-1] of the interval again to obtain a new disordered region R[1... n-2] and ordered region R[n-1... N]. Similarly, R[1... n-2] should be adjusted to heap.
• ... until there is only one element in the unordered area.
  Heap sorting heap sorting first builds a heap based on elements. Then take out the root node of the heap (generally exchange with the last node), continue the heap adjustment process for the first len-1 nodes, and then take out the root node until all nodes are taken out.

4.3 code implementation

    private static <T>void swap(T[] arr,int index1,int index2){ 
        T temp = arr[index1]; 
        arr[index1] = arr[index2]; 
        arr[index2] = temp; 
    } 
    private static <T extends Comparable<T>>void adjust(T[] arr,int start,int end){ 
        T temp=arr[start]; 
        for(int i=2*start+1;i<=end;i=2*i+1){ 
            if(i+1<=end && arr[i].compareTo(arr[i+1]) < 0){ 
                i++;//i save the subscript of the larger value of the left and right children 
                 } 
            if(temp.compareTo(arr[i]) < 0){ 
                arr[start]=arr[i]; 
                start=i; 
            }
            else{ 
                break; 
            } 
        } 
        arr[start]=temp; 
    } 
    public static <T extends Comparable<T>>void heapSort(T[] arr){ 
        int i=0; 
        for(i=(arr.length-1-1)/2;i>=0;i--){//i represents the subscript of the root node to be adjusted 
             adjust(arr, i, arr.length-1);//The maximum heap is established 
             } 
        for(i=0;i<arr.length;i++){ 
            //0 subscript root save Max  
            // arr[0] is exchanged with the opposite "last" element in the heap 
             swap(arr,0,arr.length-1-i); 
             adjust(arr, 0, arr.length-1-i-1); 
        } 
    }

4.4 algorithm analysis

• Time complexity analysis:
• Optimal time complexity: O(nlog2n) average time complexity: O(nlog2n) worst time complexity: O(nlog2n)
• Spatial complexity analysis: O(1)
• Stability analysis: unstable

5. Hill sort

5.1 Hill's idea of ranking

Hill sort is also an insertion sort, which is an improved algorithm of simple insertion sort. It also becomes an effective incremental sort. The time complexity of Hill sort is smaller than that of direct insertion sort. It differs from direct insertion sorting in that it preferentially compares distant elements. Hill sorting is to sort groups according to a certain increment, and directly insert each group. With the reduction of the number of groups, there will be more and more elements in each group. When the increment is reduced to 1, the sorting ends.

5.2 algorithm description

Select increment gap=length/2; The reduction increment continues to be grouped in the way of gap=gap/2. {n/2,(n/2)/2,(n/2)/4,..., 1} incremental sequence.

• Select an incremental sequence and sort m times according to the number of incremental sequences M.
• For each sorting, the elements are grouped according to the corresponding incremental times, and the direct insertion sorting operation is carried out in the group.
• Continue to the next increment and perform group direct insertion respectively.
• Repeat the third step until the increment becomes 1, all elements are in one group, and Hill sorting ends.

5.3 code implementation

     public static <T extends Comparable<T>>void shellSort(T[] arr,int gap){
        int i=0,j=0; 
        for(i=gap;i<arr.length;i++){ 
            T temp = arr[i];
            for(j=i-gap;j>=0;j-=gap){ 
                if(temp.compareTo(arr[j]) < 0){ 
                    arr[j+gap]=arr[j]; 
                } 
                else{ 
                    break; 
                } 
            } 
            arr[j+gap]=temp; 
        } 
    } 
    public static <T extends Comparable<T>>void shell(T[] arr){ 
        int[] partition={5,3,1};
        for(int i=0;i<partition.length;i++){ 
            shellSort(arr,partition[i]); 
        } 
    }

5.4 algorithm analysis

• Time complexity analysis: average time complexity: O(n1.3~n1.5)
• Spatial complexity analysis: O(1)
• Stability analysis: unstable

6. Merge and sort

6.1 idea of merging and sorting

Merge sort is based on the effective operation of merge. It mainly uses divide and conquer method to merge the ordered subsequences to obtain a completely ordered sequence. That is, first make each segment orderly, and then make the segments orderly. If two orders are combined into an ordered segment, it is also called two-way merging.

6.2 algorithm description

• Start merging with an interval of 1, that is, the first element is merged with the second. Merge the third with the fourth;
• Then, merge at an interval of 2, 1-4 and 5-8;
• Again, at intervals of 2 * 2, similarly, until 2*k exceeds the length of the array.
• When there are not enough two groups to merge, if there are more than k elements, merge still; If there are no more than k remaining elements, they are copied directly to the intermediate array.

6.3 code implementation

public static <T extends Comparable<T>>void merge(T[] arr,int len,int gap){ 
        int low1=0;//Starting subscript of the first merge segment 
        int high1=low1+gap-1;//End subscript of the first merge segment
        int low2=high1+1;//Starting subscript of the second merge segment 
        int high2=low2+gap-1 > len-1?len-1:low2+gap-1; 
        T[] brr=(T[])new Comparable[arr.length]; 
        int i=0; 
        while(low2 < len){//Ensure that there are two merging segments 
             while(low1<=high1 && low2<=high2){//Continue to judge when both merging segments have data 
                  if(arr[low1].compareTo(arr[low2]) <= 0){ 
                      brr[i++]=arr[low1++]; 
                  } 
                  else{ 
                      brr[i++]=arr[low2++]; 
                  } 
             } 
             while(low1<=high1){//The first merge segment also has data 
                 brr[i++]=arr[low1++]; 
             } 
             while(low2<=high2){ 
                 brr[i++]=arr[low2++]; 
             } 
             low1=high2+1; 
             high1=low1+gap-1; 
             low2=high1+1; 
             high2 = low2+gap-1 > len-1?len-1:low2+gap-1; 
        } 
        //There are no two merge segments: single copy directly 
         while(low1<=len-1){ 
             brr[i++]=arr[low1++]; 
         } 
         for(i=0;i<arr.length;i++){ 
             arr[i]=brr[i];
         }
         brr=null; 
    } 
    public static <T extends Comparable<T>>void mergeSort(T[] arr){ 
        for(int i=1;i<arr.length;i*=2){//Two, two, four, four 
             merge(arr,arr.length,i); 
        } 
    }

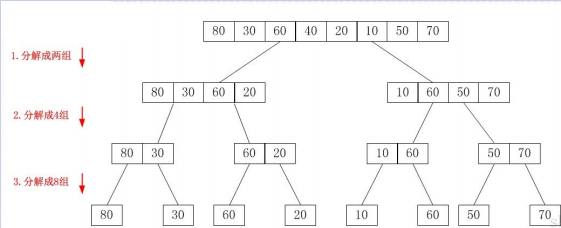
6.4 algorithm analysis

• Time complexity analysis: average time complexity: O(nlog2n) worst time complexity: O(nlog2n)
• Spatial complexity analysis: O(n)
• Stability analysis: stability

7. Quick sort

7.1 idea of quick sort

Fast scheduling is mainly by selecting a key value as the reference value. The sequence smaller than the benchmark value is on the left (generally unordered), and the sequence larger than the benchmark value is on the right (generally unordered). Recursion is based on this, so that the overall sequence to be sorted is orderly.

7.2 algorithm description

• Select benchmark: in the sequence to be arranged, select an element in a certain way as the "pivot"
• Segmentation operation: divide the sequence into two subsequences based on the actual position of the benchmark in the sequence. At this time, the elements on the left of the benchmark are smaller than the benchmark, and the elements on the right of the benchmark are larger than the benchmark
• Two sequences are quickly sorted recursively until the sequence is empty or has only one element.

7.3 code implementation

Three digit median

 //random
    //Median three digit median
    public static int RandParition(int []arr,int left,int right){
        Random random=new Random();
        int index=random.nextInt((right-left)+1)+left;
        int tmp=arr[left];
        arr[left]=arr[index];
        arr[index]=tmp;
        return Parition(arr,left,right);
    }
    public static void QuickSort(int []arr){
        QuickPass(arr,0,arr.length-1);
    }
    public static int Parition(int []arr,int left,int right){
        int i=left,j=right;
        int tmp=arr[i];
        while (i<j){
            while (i<j&&arr[j]>tmp)--j;
            if(i<j)arr[i]=arr[j];
            while (i<j&&arr[i]<=tmp)++i;
            if(i<j)arr[j]=arr[i];
        }
        arr[i]=tmp;
        return i;
    }

non-recursive

     public static void QuickPass(int []arr,int left,int right) {
         Queue<Integer> queue = new LinkedList<>();
         if (left >= right) return;
         queue.offer(left);
         queue.offer(right);
         while (!queue.isEmpty()) {
             left = queue.poll();
             right = queue.poll();
             int pos = OWParition2(arr, left, right);
             if (left < pos - 1) {
                 queue.offer(left);
                 queue.offer((pos - 1));
             }
             if (pos + 1 < right) {
                 queue.offer(pos + 1);
                 queue.offer(right);
             }
         }
     }
     public static int OWParition2(int []arr,int left,int right){
        int i=left,j=left+1;
        int tmp=arr[i];
        while (j<=right){
            if(arr[j]<=tmp){
                i+=1;
               Swap(arr,i,j);
            }
                j++;
        }
        Swap(arr,left,i);
        return  i;
    }
    public static void Swap(int[]arr,int i,int j){
        int tmp=arr[i];
        arr[i]=arr[j];
        arr[j]=tmp;
    }

recursion

public static void QuickSort(int []arr){
        QuickPass(arr,0,arr.length-1);
    }
    //    Using recursion
    public static void QuickPass(int []arr,int left,int right){
        if(left<right){
            int pos=Parition(arr,left,right);
            QuickPass(arr,left,pos-1);
            QuickPass(arr,pos+1,right);
        }
    }
     public static int Parition(int []arr,int left,int right){
        int i=left,j=right;
        int tmp=arr[i];
        while (i<j){
            while (i<j&&arr[j]>tmp)--j;
            if(i<j)arr[i]=arr[j];
            while (i<j&&arr[i]<=tmp)++i;
            if(i<j)arr[j]=arr[i];
        }
        arr[i]=tmp;
        return i;
    }

7.4 algorithm analysis

• Time complexity analysis:
  Optimal time complexity: O(nlog2n) average time complexity: O(nlog2n) worst time complexity: O(nlog2n)
• Spatial complexity analysis: Olog2n)
• Stability analysis: unstable