Tree structure foundation

I. overview

Why tree data structure is needed:

• Tree storage can improve the efficiency of data storage and reading. For example, by using * * binary sort tree, * * can not only ensure the speed of data retrieval, but also the speed of data insertion, deletion and modification

Common terms for trees:

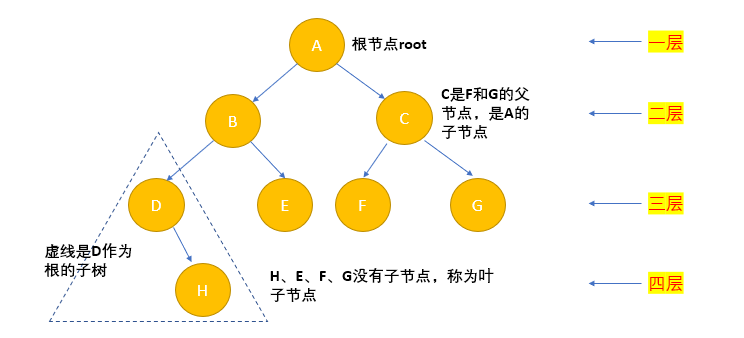
• Node weight (node value)
• Path (path from root to the larger node)
• Height of tree (maximum layers)
• Forest: the structure of many trees makes up the forest

2, Binary tree

1. overview

1. Each node can only have one form of two child nodes at most
2. The sub nodes of binary tree are divided into left node and right node

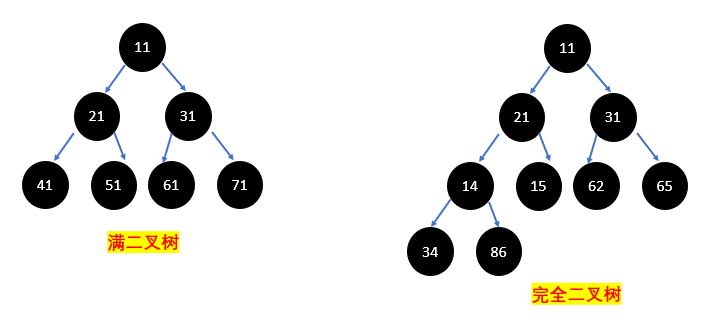
1. If all nodes of the binary tree are at the last level, and the total number of nodes is 2^n-1(n is the number of layers), it is called a full binary tree
2. If all the leaf nodes of the binary tree are in the last layer or the penultimate layer, and the last layer of leaf nodes are continuous on the left, and the penultimate layer of leaf nodes are continuous on the right, we call it a complete binary tree

2. Traversal of binary tree

Use pre order, middle order and post order to traverse the binary tree:

• Preorder traversal: first output the parent node, then traverse the left and right subtrees
• Middle order traversal: first traverse the left subtree, then output the parent node, and then traverse the right subtree
• Post order traversal: first traverses the right subtree, then traverses the right subtree, and finally outputs the parent node

class Node{
    private int no;
    private String name;
    private Node left;
    private Node right;

    public Node(int no, String name) {
        this.no = no;
        this.name = name;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public void setRight(Node right) {
        this.right = right;
    }

    public int getNo() {
        return no;
    }

    public void setNo(int no) {
        this.no = no;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    @Override
    public String toString() {
        return "Node{" +
                "no=" + no +
                ", name='" + name + '\'' +
                '}';
    }

    /**
     * Preorder traversal
     */
    public void preOrder(){
        System.out.println(this);
        if(this.left!=null){
            this.left.preOrder();
        }
        if(this.right!=null){
            this.right.preOrder();
        }
    }

    /**
     * Sequential traversal
     */
    public void infixOrder(){
        if(this.left!=null){
            this.left.infixOrder();
        }
        System.out.println(this);
        if(this.right!=null){
            this.right.infixOrder();
        }
    }

    /**
     * Post order traversal
     */
    public void postOrder(){
        if(this.left!=null){
            this.left.postOrder();
        }
        if(this.right!=null){
            this.right.postOrder();
        }
        System.out.println(this);
    }
}

3. search

class Node{	
	/**
     * Preorder traversal search
     *
     * @param no
     * @return
     */
    public Node preOrderSearch(int no) {
        if (root != null) {
            return root.preOrderSearch(no);
        } else {
            return null;
        }
    }

    /**
     * Middle order traversal search
     *
     * @param no
     * @return
     */
    public Node infixOrderSearch(int no) {
        if (root != null) {
            return root.infixOrderSearch(no);
        } else {
            return null;
        }
    }

    /**
     * Postorder traversal search
     *
     * @param no
     * @return
     */
    public Node postOrderSearch(int no) {
        if (root != null) {
            return root.postOrderSearch(no);
        } else {
            return null;
        }
    }
}

4. delete

Explain:

• If the deleted node is a leaf node, delete the node
• If you delete a non leaf node, delete the subtree

class Node{
	/**
     * Delete node
     * @param no Node number
     */
    public void delNode(int no){
        if(this.left!=null&&this.left.no==no){
            this.left=null;
            return;
        }
        if(this.right!=null&&this.right.no==no){
            this.right=null;
            return;
        }
        if(this.left!=null){
            this.left.delNode(no);
        }
        if(this.right!=null){
            this.right.delNode(no);
        }
    }
}

3, Sequential storage binary tree

1. overview

Explain:

From the perspective of data storage, array storage and tree storage can transform each other. That is, arrays can be converted to trees and trees can also be converted to arrays.

Characteristic:

• In general, only complete binary trees are considered in order binary trees
• The left child node of the nth element is 2*n+1
• The right child node of the nth element is 2*n+2
• The parent node of the nth element is (n-1)/2
• n: Represents the second element in the binary tree (numbered from 0)

2. Code demonstration

/**
 * @author DELL
 * @Date 2020/2/6 17:19
 **/
public class ArrayBinaryTreeDemo {
    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5, 6, 7};
        ArrayBinaryTree arrayBinaryTree = new ArrayBinaryTree(arr);
        arrayBinaryTree.preOrder();
    }
}

class ArrayBinaryTree {
    private int[] arr;

    public ArrayBinaryTree(int[] arr) {
        this.arr = arr;
    }

    /**
     * Overload preOrder method
     */
    public void preOrder() {
        this.preOrder(0);
    }

    /**
     * @param index Subscript of array
     */
    public void preOrder(int index) {
        if (arr == null || arr.length == 0) {
            System.out.print("Array is empty!");
        }
        System.out.println(arr[index]);
        if ((index * 2 + 1) < arr.length) {
            preOrder(2 * index + 1);
        }
        if ((index * 2 + 2) < arr.length) {
            preOrder(2 * index + 2);
        }
    }
}

4, Clue binary tree

1. overview

• The binary list of N nodes contains n+1 [(2n-(n-1))] empty pointer fields. Using the empty pointer domain in the binary list to store the pointer to the predecessor and successor nodes of the node in a certain traversal order
• The binary list with clues is called the clue binary list, and the corresponding binary tree is called the clue binary tree. According to the different properties of clues, the clue binary tree can be divided into three types: the pre order clue binary tree, the middle order clue binary tree and the post order clue binary tree
• The previous node of a node is called the precursor node
• The next node of a node is called the successor node

2. Application cases

• For example, the result of a binary tree is: {8, 3, 10, 1, 14, 6}
• After cueing, the attribute left of Node points to the left subtree or the precursor Node, and the attribute right points to the right subtree or the successor Node

class ThreadedBinaryTree {
    private Node root;
    private Node pre=null;
    public void setRoot(Node root) {
        this.root = root;
    }
    public void threadNodes(){
        this.threadNodes(root);
    }
    /**
     * Cue
     * @param node
     */
    public void threadNodes(Node node){
        if(node==null){
            return;
        }
        //Clue left subtree
        threadNodes(node.getLeft());
        //Clue current node
        if(node.getLeft()==null){
            node.setLeft(pre);
            node.setLeftType(1);
        }
        //Processing subsequent nodes
        if(pre!=null&&pre.getRight()==null){
            //Let the pointer of the precursor node point to the current node
            pre.setRight(node);
            pre.setRightType(1);
        }
        pre=node;
        //Clue right subtree
        threadNodes(node.getRight());
    }
}

3. traversal

class Node{
	/**
     * Traversing threaded binary tree
     */
    public void threadedList(){
        Node node=root;
        while(node!=null){
            //Loop to find the node with leftType==1, when leftType==1
            // This node is an effective node after processing according to clues
            while(node.getLeftType()==0){
                node=node.getLeft();
            }
            System.out.println(node.toString());
            //If the right pointer of the current node points to the successor node, it will output all the time
            while(node.getRightType()==1){
                //Get the successor node of the current node
                node=node.getRight();
                System.out.println(node.toString());
            }
            //Replacement node
            node=node.getRight();
        }
    }
}