1, TreeSet
1. The bottom layer of TreeSet set is actually a TreeMap; At the bottom of the TreeMap set is a binary tree
2. The elements put into the TreeSet set are equivalent to the key part of the TreeMap set.
3. TreeSet set storage element features: unordered and non repeatable, but the stored elements can be automatically sorted in size order
Called: sortable set.
Disorder means that the order of saving is different from that of taking out, and there is no subscript
TreeSet source code storage element: it is actually the put method of the called TreeMap
public TreeSet() {
this(new TreeMap<E,Object>());
}
public boolean add(E e) {
return m.put(e, PRESENT)==null;
}Elements stored in TreeMap:
public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e);
size++;
modCount++;
return null;
}TreeMap fetch element:
public V get(Object key) {
Entry<K,V> p = getEntry(key);
return (p==null ? null : p.value);
}
final Entry<K,V> getEntry(Object key) {
// Offload comparator-based version for sake of performance
if (comparator != null)
return getEntryUsingComparator(key);
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
return null;
}The tests are as follows:
public static void main(String[] args) {
TreeSet<String> set = new TreeSet<>();
set.add("A");
set.add("D");
set.add("F");
set.add("B");
set.add("G");
set.add("E");
set.add("C");
for (String str: set) {
System.out.println(str);
/*
A
B
C
D
E
F
G
*/
}
// Create a TreeSet collection
TreeSet<String> ts = new TreeSet<>();
// Add String
ts.add("zhangsan");
ts.add("lisi");
ts.add("wangwu");
ts.add("zhangsi");
ts.add("wangliu");
// ergodic
for(String s : ts){
// In dictionary order, ascending order!
System.out.println(s);
/*
lisi
wangliu
wangwu
zhangsan
zhangsi
*/
}
TreeSet<Integer> ts2 = new TreeSet<>();
ts2.add(100);
ts2.add(200);
ts2.add(900);
ts2.add(800);
ts2.add(600);
ts2.add(10);
for(Integer elt : ts2){
// Ascending order!
System.out.println(elt);
/*
10
100
200
600
800
900
*/
}2, Comparator
1. There are two sorts in TreeSet: one is natural sort, and the other is custom sort by overriding compareTo() method.
Natural sorting can refer to the implementation of Integer, String and other classes. The order is also our common "1,2,3,4", "a,b,c,d".
2. Override the compareTo() method to customize sorting
(1) For custom types, TreeSet cannot sort because no comparison rules between custom type objects are specified
An exception occurred while the program was running:
java.lang.ClassCastException: class com.collection.XX cannot be cast to class
java. The reason for this exception in lang. comparable is that the custom type object does not implement Java Lang. comparable interface
As follows:
public class TreeSetCustom {
public static void main(String[] args) {
TreeSet<TreeSetPerson> set = new TreeSet<>();
TreeSetPerson p1 = new TreeSetPerson(28);
TreeSetPerson p2 = new TreeSetPerson(12);
TreeSetPerson p3 = new TreeSetPerson(24);
TreeSetPerson p4 = new TreeSetPerson(16);
set.add(p1);
set.add(p2);
set.add(p3);
set.add(p4);
for (TreeSetPerson person:set) {
System.out.println(person);
}
}
}
class TreeSetPerson {
private int age;
public TreeSetPerson(){
}
public TreeSetPerson(int age){
this.age = age;
}
@Override
public String toString(){
return "TreeSetPerson[age="+ this.age + "]";
}
}
3. The elements in the TreeSet collection can be sorted in two ways:
(1) The elements placed in the collection implement Java Lang. comparable interface
(2) When constructing a TreeSet or TreeMap set, a Comparator object Comparator is passed to the
TreeSet provides four constructors
TreeSet() TreeSet(Collection< ? extends E> c) TreeSet(Comparator< ? super E> comparator) TreeSet(SortedSet< E > s)
(1) Implement Java Lang. comparable interface
/**
compareTo Return value of method:
Returning 0 means the same, and value will overwrite
If > 0 is returned, it will continue to find on the right subtree
If < 0 is returned, it will continue to find on the left subtree
*/
public class TreeSetCustom1 {
public static void main(String[] args) {
TreeSet<TreeSetPeople> peopleSet = new TreeSet<>();
//First in ascending order by age, and then in ascending order by name if the age is the same
TreeSetPeople p1 = new TreeSetPeople(20,"Zhang San");
TreeSetPeople p2 = new TreeSetPeople(12,"Li Si");
TreeSetPeople p3 = new TreeSetPeople(24,"WangTwo ");
// In dictionary order, ascending order!
TreeSetPeople p4 = new TreeSetPeople(18,"Zhao Si");//zhaosi
TreeSetPeople p5 = new TreeSetPeople(18,"Liu San");//liusan
TreeSetPeople p6 = new TreeSetPeople(16,"Qian Yi");
peopleSet.add(p1);
peopleSet.add(p2);
peopleSet.add(p3);
peopleSet.add(p4);
peopleSet.add(p5);
peopleSet.add(p6);
for(TreeSetPeople people:peopleSet){
System.out.println(people);
}
}
}
/**
The elements placed in the TreeSet collection need to implement Java Lang. comparable interface.
Implement compareTo method
* */
class TreeSetPeople implements Comparable<TreeSetPeople>{
private int age;
private String name;
public TreeSetPeople(){
}
public TreeSetPeople(int age,String name){
this.age = age;
this.name = name;
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
@Override
public String toString(){
return "TreeSetPeople[age=" + this.age + ","
+ "name=" + this.name + "]";
}
/**
* You need to write sorting rules in this method and compare them according to what
* k.compareTo(t.key)
* Compare the parameter k with each k in the set
* */
@Override
public int compareTo(TreeSetPeople o) {
if (this.age == o.age){
return this.name.compareTo(o.name);
}else {
return this.age - o.age;
}
}
}(2) Comparator object comparator
public class TreeSetComparatorTest {
public static void main(String[] args) {
// TreeSet<Child> childTreeSets = new TreeSet<>(new ChildComparator());
TreeSet<Child> childTreeSets = new TreeSet<>(new Comparator<Child>() {
@Override
public int compare(Child o1, Child o2) {
return o1.getAge() - o2.getAge();
}
});
Child c1 = new Child(10);
Child c2 = new Child(6);
Child c3 = new Child(2);
Child c4 = new Child(8);
childTreeSets.add(c1);
childTreeSets.add(c2);
childTreeSets.add(c3);
childTreeSets.add(c4);
for (Child c : childTreeSets){
System.out.println(c);
}
}
}
class Child{
private int age;
public Child(int age){
this.age = age;
}
@Override
public String toString(){
return "Child[age=" + this.age + "]";
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
}
class ChildComparator implements Comparator<Child>{
@Override
public int compare(Child o1, Child o2) {
return o1.getAge() - o2.getAge();
}
}4. Comparable and Comparator selection
When the comparison rules will not change (when there is only one comparison rule), the Comparable interface can be implemented
If there are multiple comparison rules and frequent switching between multiple comparison rules is required, the Comparator interface can be used
3, Binary tree
1. Teet/TreeMap is a self balanced binary tree (AVL), which is stored according to the principle of small left and large right
Storage depends on the principle of small left and large right, and comparison shall be made during storage
2. Three ways to traverse binary tree
(1) Preorder traversal: left and right roots
(2) Middle order traversal: left root right
(3) Post order traversal: left and right roots
Note:
The former, the middle and the latter say the position of the "root"
The root in front is the preamble; The root in the middle is the middle order; After the root is the order
3. TreeSet set / TreeMap set adopts the medium order traversal method (left root right)
Iterator iterator adopts the medium order traversal mode
The process of storing is the process of sorting, and taking out is automatically arranged according to the size order
The following data:
5 2 8 1 4 7 9 3
In the binary tree, it is represented as follows:
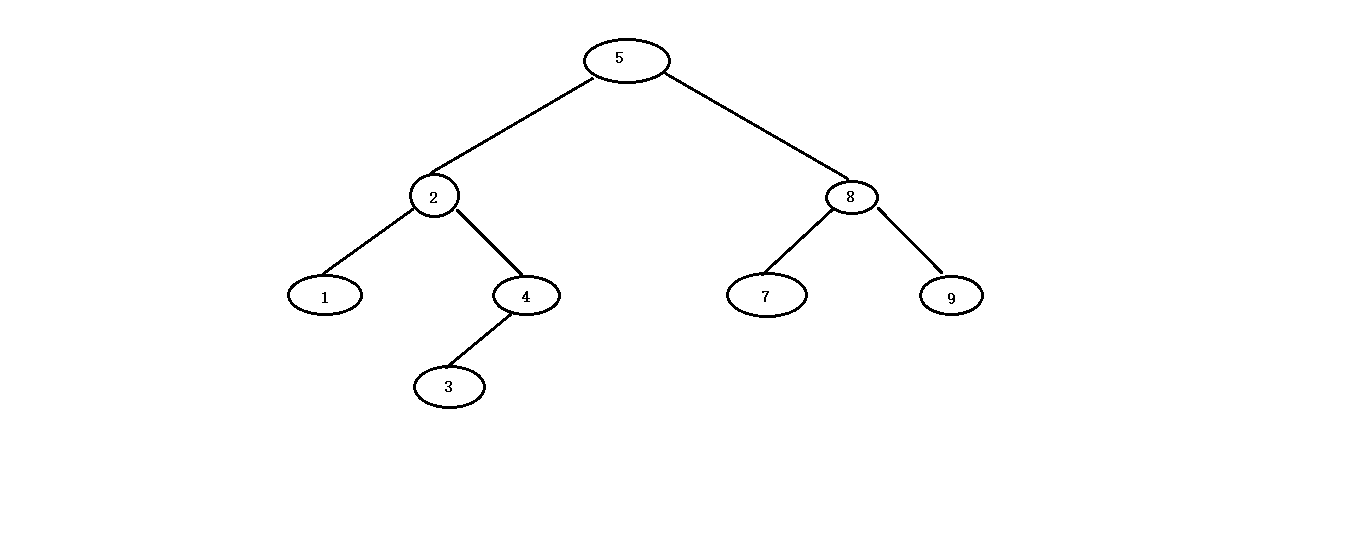
In the middle order traversal mode (left and right), you will get
1 # 2 # 3 # 8
If you want to deeply study the binary tree data structure, you can refer to the books related to data structure