104. Maximum depth of binary tree

Left and right nodes are recursive, and + 1 if there are nodes;

• DFS} bottom-up recursion

var maxDepth = function(root) {
    if(root==null)return 0;
    let maxleft = maxDepth(root.left);
    let maxright=maxDepth(root.right);
    return Math.max(maxleft,maxright)+1;
};

              

Recursive three parts:

1. Determine the parameters and return values of the recursive function;

2. Determine termination conditions;

3. Determine the logic of single-layer recursion.

Tree traversal to find depth

           

226. Flip binary tree

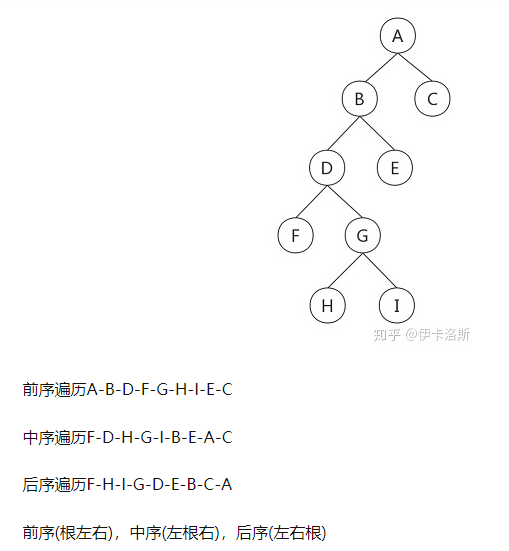
Recursive trilogy!

var invertTree = function(root) {
    if(root==null)return null;
    const p = root.left;
    root.left=invertTree(root.right);
    root.right=invertTree(p);
    return root;

};

617. Merge binary tree

var mergeTrees = function(root1, root2) {
    if(root1==null) return root2;
    if(root2==null) return root1;
    root1.val += root2.val;
    root1.left = mergeTrees(root1.left,root2.left);
    root1.right = mergeTrees(root1.right,root2.right);
    return root1;
};

108. Convert an ordered array into a binary search tree

Search tree divide and rule.

Array value subscript, math Floor (left + (right left) / 2), left and right refer to subscripts, e.g. 0, len-1;

Termination condition!!!!

New node let root = new treenode (Num [mid]);

var sortedArrayToBST = function(nums) {
    if(nums.length==0)return null;
    let mid = Math.floor(nums.length/2);
    let root = new TreeNode(nums[mid]);
    root.left = sortedArrayToBST(nums.slice(0,mid));
    root.right = sortedArrayToBST(nums.slice(mid+1));
    return root;
};

100. Same tree

var isSameTree = function(p, q) {
    if(p==null&&q==null)return true;
    if(q&&p&&p.val==q.val){
        return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
    }
    else{
        return false;
    }
};

669. Pruning binary search tree

Return logic of each layer

var trimBST = function(root, low, high) {
    if(root==null) return null;
    if(root.val>high){return trimBST(root.left,low,high);}   
    if(root.val<low){return trimBST(root.right,low,high);}
    root.left = trimBST(root.left,low,high);
    root.right = trimBST(root.right,low,high);
    return root;

};

110. Balanced binary tree

If you don't write it out, you have to construct another function.

The depth is suitable for pre order traversal, and the height is suitable for post order traversal.

Use recursive trilogy + Post sequence to traverse the current left subtree and right subtree in the left and right. If the height difference is greater than 1, it returns - 1

var isBalanced = function(root) {
    const deepth=function(r){
        if(r==null) {return 0};
        let dl= deepth(r.left);
        if(dl==-1){return -1;}
        let dr = deepth(r.right);
        if(dr==-1){return -1;}
        if(Math.abs(dl-dr)>1){return -1;}
        else{return Math.max(dl,dr)+1;}
}
    return deepth(root)==-1?false:true;

};

1. Determine parameters and return values;

The return value returns the depth of the tree where the incoming node is the root node.

So how to mark whether the difference between the left and right subtrees is greater than 1? I didn't think of two contradictions

If the binary tree with the current incoming node as the root node is no longer a binary balanced tree and returns the height, it is meaningless.

Therefore, if it is no longer a binary balanced tree, you can return - 1 to mark that it does not comply with the rules of the balanced tree.

101. Symmetric binary tree
 

I didn't think of it. The outer layer is symmetrical and the inner layer is symmetrical

If you create a new function, the original function must reference the new function.

New functions can be placed inside or outside.

var isSymmetric = function(root) {
    if(root==null)return true;
//Determine the recursive parameter root left root. Right and return values true and false 
    const campare = function(r,l){
//Termination conditions
        if(r==null&&l==null) return true;
        else if(r==null)return false;
        else if(l==null)return false;
        else if(r.val != l.val)return false;
//Single layer logic
        let outside = campare(l.left,r.right);
        let inside  =campare(l.right,r.left);
        return outside&&inside;
    }
    return campare(root.right,root.left);
};

Iterative method, using pairs of columns or stacks,

var isSymmetric = function(root) {
    if(root==null)return true;
    let que =[];
    que.push(root.left);
    que.push(root.right);
    while(que.length){
        let leftNode = que.shift();
        let rightNode= que.shift();
        if(leftNode==null&&rightNode==null)continue;
        else if(leftNode==null||rightNode==null||leftNode.val!=rightNode.val)return false;
        que.push(leftNode.left);
        que.push(rightNode.right);
        que.push(leftNode.right);
        que.push(rightNode.left);
    }
    return true;
};

235. Nearest common ancestor of binary search tree

Written by myself, the code doesn't look concise.

var lowestCommonAncestor = function(root, p, q) {
    const findRoot=function(r,v,f){
        f.push(r);
        if(v.val>r.val){return findRoot(r.right,v,f);}
        if(v.val<r.val){return findRoot(r.left,v,f);}
        if(v.val==r.val){return f;} 
    }
    let fp=[];
    let fq=[];
    let pf = findRoot(root,p,fp);
    let qf = findRoot(root,q,fq);
    let res =0;
    while(pf.length||qf.length){
        let vp = pf.length?pf.shift():0;
        let vq = qf.length?qf.shift():0;
        if(vp==vq){res =vp;}
        if(vp!=vq) {break;}      
    }
    return res;
};

Because the idea of solving problems is complex.

You should compare the sizes of P and Q with the current root. When P and Q are on both sides of the current root, they are the nearest node.

Iterative method

var lowestCommonAncestor = function(root, p, q) {
    while(root){
        if((p.val<=root.val&&q.val>=root.val)||(q.val<=root.val&&p.val>=root.val))return root;
        else if(p.val<=root.val&&q.val<=root.val) {root = root.left;}
        else if(p.val>=root.val&&q.val>=root.val) {root = root.right;}
    }
};