This paper introduces the basic algorithm and advanced algorithm of data sorting. These algorithms only rely on arrays to store data.

Array test platform

First, we construct an array test platform class

function CArray(numElements) {
    this.dataStore = [];
    this.numElements = numElements;
    this.toString = toString;
    this.clear = clear;
    this.setData = setData;
    this.swap = swap;
}
function setData() {
    for (var i = 0; i < this.numElements; ++i) {
    this.dataStore[i] = Math.floor(Math.random() * (this.numElements + 1));
    }
}
function clear() {
    for (var i = 0; i < this.numElements; ++i) {
    this.dataStore[i] = 0;
    }
}
function toString() {
    var restr = "";
    for (var i = 0; i < this.numElements; ++i) {
    restr += this.dataStore[i] + " ";
    if (i > 0 && i % 10 == 0) {
        restr += "\n";
    }
    }
    return restr;
}
function swap(arr, index1, index2) {
    var temp = arr[index1];
    arr[index1] = arr[index2];
    arr[index2] = temp;
}

Use test platform class

var numElements = 100;
var myNums = new CArray(numElements);
myNums.setData();
console.log(myNums.toString());

Basic sorting algorithm

These algorithms are very realistic to simulate the sorting of data in real life.

Bubble sort

It is one of the slowest sorting algorithms, but also one of the easiest to implement. Bubble sorting is called because when using this sort algorithm, data values float from one end of the array to the other like bubbles. Suppose you are sorting a set of numbers in ascending order, the larger values float to the right of the array, and the smaller values float to the left of the array. The reason for this phenomenon is that the algorithm will move in the array many times, compare the adjacent data, and exchange them when the left value is greater than the right value.

Bubble sort code

function bubbleSort() {
    var numElements = this.dataStore.length;
    for (var outer = numElements; outer >= 2; --outer) {
        for (var inner = 0; inner < outer - 1; ++inner) {
            if (this.dataStore[inner] > this.dataStore[inner + 1]) {
                this.swap(this.dataStore, inner, inner + 1);
            }
        }
    }
}

Sorting process (manually entered test data) The outer loop limits the unsorted range (from numElements to 2). The inner loop starts to compare and exchange the data on the left side step by step, so that the largest number in the unsorted range moves to the right side, and the outer loop continues to shrink until there are two unsorted elements left, and then the comparison and exchange completes the sorting

Selection sort

Select sort to start at the beginning of the array, comparing the first element with other elements. After checking all the elements, the smallest element is placed in the first position of the array, and then the algorithm continues from the second position. This process goes on all the time. When it reaches the penultimate position of the array, all the data is sorted.

function selectionSort() {
    var min;
    for (var outer = 0; outer <= this.dataStore.length - 2; ++outer) {
        min = outer;
        for (var inner = outer + 1; inner <= this.dataStore.length - 1; ++inner) {
            if (this.dataStore[inner] < this.dataStore[min]) {
                min = inner;
            }
        }
        swap(this.dataStore, outer, min);
    }
}

Sorting process

Insertion sort

The insertion sort has two loops. The outer loop moves array elements one by one, while the inner loop compares the selected elements in the outer loop. If the selected element in the outer loop is smaller than the selected element in the inner loop, the array element moves to the right to make room for this element in the inner loop.

function insertionSort() {
    var temp, inner;
    for (var outer = 1; outer <= this.dataStore.length - 1; ++outer) {
    temp = this.dataStore[outer];
    inner = outer;
    while (inner > 0 && (this.dataStore[inner - 1] >= temp)) {
        this.dataStore[inner] = this.dataStore[inner - 1];
        --inner;
    }
    this.dataStore[inner] = temp;
    }
}

Timing comparison of basic sorting algorithms

10000 random number tests

bubbleSort();// About 100ms
selectionSort();// About 50ms
insertionSort();// About 27ms

Selection sorting and insertion sorting are faster than bubble sorting. Insertion sorting is the fastest of the three algorithms.

Advanced sorting algorithm

Shell Sort

Hill sort has made great improvement on the basis of insertion sort. It first compares elements that are far away, not adjacent elements. This allows elements that are far from the right location to return to the right location more quickly. When the algorithm is used to traverse the data set, the distance between all elements will continue to decrease until the end of the data set is processed. At this time, the algorithm compares adjacent elements. Hill sorting works by defining a sequence of intervals to show how far apart elements are compared during sorting. We can define interval sequence dynamically, but the interval sequence used in most scene algorithms can be defined in advance. The interval sequence defined by Marchin Ciura in a published paper is 701301132,57,23,10,4,1. Here we use a small data set to see how the algorithm works.

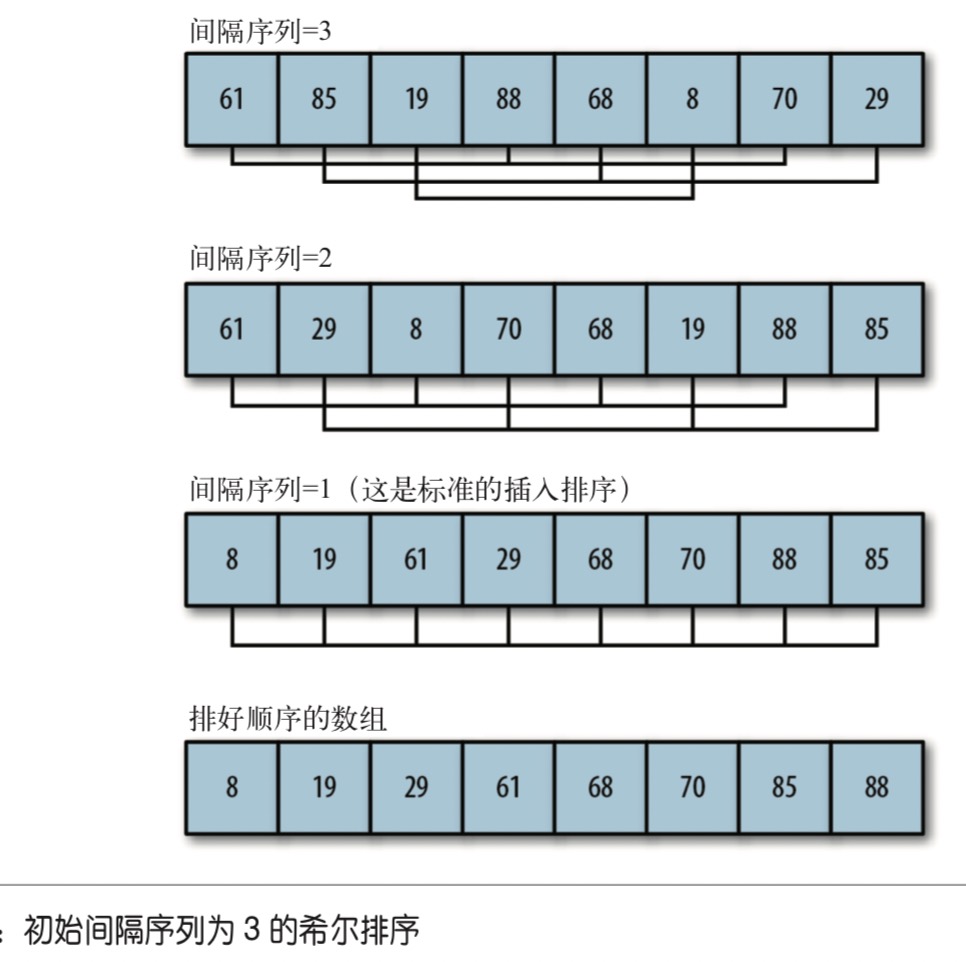
function shellsort() {
    var temp;
    for (var g = 0; g < this.gaps.length; ++g) {
    for (var i = this.gaps[g]; i < this.dataStore.length; ++i) {
        temp = this.dataStore[i];
        for (var j = i; j >= this.gaps[g] && this.dataStore[j-this.gaps[g]] > temp; j -= this.gaps[g]) {
        this.dataStore[j] = this.dataStore[j - this.gaps[g]];
        }
        this.dataStore[j] = temp;
    }
    }
}

We need to add the definition of interval sequence in the curray class:

this.gaps = [5,3,1];

Calculate dynamic interval sequence

Sedgewick's algorithm determines the initial interval value through the following code snippet:

var N = this.dataStore.length;
var h = 1;
while (h < N/3) {
    h = 3 * h + 1;
}

After the interval value is determined, the function can run like the shellsort() function defined previously. The only difference is that the last statement before the outer loop is returned to calculate a new interval value:

h = (h-1)/3;

Hill ordering of interval sequences in dynamic computation

function shellsort1() {
    var N = this.dataStore.length;
    var h = 1;
    while (h < N/3) {
        h = 3 * h + 1;
    }
    while (h >= 1) {
        for (var i = h; i < N; i ++) {
            for (var j = i; j >= h && this.dataStore[j] < this.dataStore[j-h]; j -= h) {
                this.swap(this.dataStore, j, j - h);
            }
        }
        h = (h-1)/3;
    }
}

For the sorting test of 10000 random numbers:

myNums.shellsort(); // About 20ms
myNums.shellsort1(); // About 8ms

Merge sort

Merge sort merges a series of ordered subsequences into a large complete ordered sequence. We need two ordered subarrays, and then by comparing the data size, we start with the smallest data, and finally merge to get the third array. However, in practice, there are still some problems in merging and sorting. We need more space to merge and store two subarrays.

Bottom up merge sort Generally speaking, merge sorting is implemented by recursive algorithm. In JavaScript, however, this approach is not feasible because the depth of recursion is too deep. Therefore, we use a non recursive way to implement this algorithm, which is called bottom-up merge sorting. This algorithm first decomposes the data set into an array with only one element. Then create a set of left and right subarrays to merge them slowly. Each time, some sorted data will be saved until all the data of the last remaining array has been sorted perfectly. Algorithm code

function mergeSort() {
    var arr = this.dataStore;
    if (arr.length < 2) {
    return;
    }
    var step = 1;
    var left, right;
    while (step < arr.length) {
    left = 0;
    right = step;
    while (right + step <= arr.length) {
        this.mergeArrays(arr, left, left+step, right, right+step);
        left = right + step;
        right = left + step;
    }
    if (right < arr.length) {
        this.mergeArrays(arr, left, left+step, right, arr.length);
    }
    step *= 2;
    }
}

function mergeArrays(arr, startLeft, stopLeft, startRight, stopRight) {
    var rightArr = new Array(stopRight - startRight + 1);
    var leftArr = new Array(stopLeft - startLeft + 1);
    k = startRight;
    for (var i = 0; i < (rightArr.length-1); ++i) {
    rightArr[i] = arr[k];
    ++k;
    }
    k = startLeft;
    for (var i = 0; i < (leftArr.length-1); ++i) {
    leftArr[i] = arr[k];
    ++k;
    }
    rightArr[rightArr.length - 1] = Infinity;
    leftArr[leftArr.length - 1] = Infinity;
    var m = 0;
    var n = 0;
    for (var k = startLeft; k < stopRight; ++k) {
    if (leftArr[m] <= rightArr[n]) {
        arr[k] = leftArr[m];
        m++;
    } else {
        arr[k] = rightArr[n];
        n++;
    }
    }
}

Quick sort

Fast sorting is one of the fastest sorting algorithms for large data sets. It is a divide and conquer algorithm, which decomposes the data into different subsequences containing smaller and larger elements by recursion. The algorithm repeats this step until all data is in order. The algorithm first selects an element in the list as the pivot. Data sorting revolves around the benchmark value, moving the elements less than the benchmark value in the list to the bottom of the array, and moving the elements greater than the benchmark value to the top of the array.

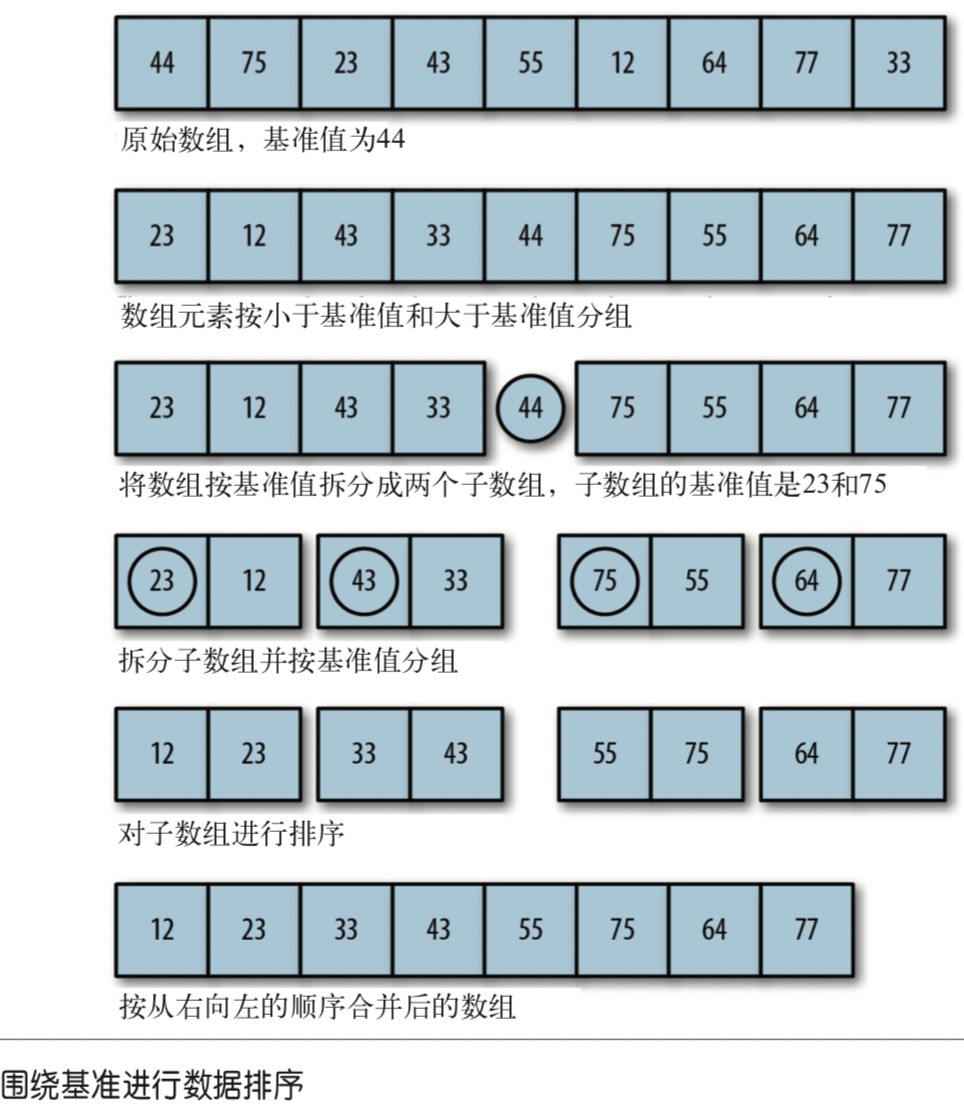
Algorithm pseudocode

1. Select a datum element to separate the list into two subsequences
2. Reorder the list, putting all elements less than the benchmark value before the benchmark value, and all elements greater than the benchmark value after the benchmark value
3. Repeat steps 1 and 2 for the subsequence of the smaller element and the subsequence of the larger element, respectively The procedure is as follows:

function qSort(list) {
    var list;
    if (list.length == 0) {
        return [];
    }
    var lesser = [];
    var greater = [];
    var pivot = list[0];
    for (var i = 1; i < list.length; i ++) {
        if (list[i] < pivot) {
        lesser.push(list[i]);
        } else {
        greater.push(list[i]);
        }
    }
    return this.qSort(lesser).concat(pivot, this.qSort(greater));
}

Output the sorting process before the qSort function returns

console.log(lesser.concat(pivot, greater).toString());

10000 random number sequencing tests

qSort(); // About 17ms

Fast sorting algorithm is very suitable for large data sets, but its performance will decrease when dealing with small data sets.

(attached) test platform code

<!DOCTYPE html>
<html lang="en">
<head>
</head>
<body>
  <script>
    function CArray(numElements) {
      // this.dataStore = [72, 54, 58, 30, 31, 78, 2, 77, 82, 72];
      this.dataStore = [];
      // this.dataStore = [44, 75, 23, 43, 55, 12, 64, 77 ,33];
      this.numElements = numElements;
      this.toString = toString;
      this.clear = clear;
      this.setData = setData;
      this.swap = swap;
      this.bubbleSort = bubbleSort;
      this.selectionSort = selectionSort;
      this.insertionSort = insertionSort;
      this.shellsort = shellsort;
      this.shellsort1 = shellsort1;
      this.mergeSort = mergeSort;
      this.mergeArrays = mergeArrays;
      this.qSort = qSort;
      this.gaps = [5, 3, 1];
    }
    function setData() {
      for (var i = 0; i < this.numElements; ++i) {
        this.dataStore[i] = Math.floor(Math.random() * (this.numElements + 1));
      }
    }
    function clear() {
      for (var i = 0; i < this.numElements; ++i) {
        this.dataStore[i] = 0;
      }
    }
    function toString() {
      var restr = "";
      for (var i = 0; i < this.numElements; ++i) {
        restr += this.dataStore[i] + " ";
        if (i > 0 && i % 10 == 0) {
          restr += "\n";
        }
      }
      return restr;
    }
    function swap(arr, index1, index2) {
      var temp = arr[index1];
      arr[index1] = arr[index2];
      arr[index2] = temp;
    }
    function selectionSort() {
        var min;
        for (var outer = 0; outer <= this.dataStore.length - 2; ++outer) {
            min = outer;
            for (var inner = outer + 1; inner <= this.dataStore.length - 1; ++inner) {
                if (this.dataStore[inner] < this.dataStore[min]) {
                    min = inner;
                }
            }
            swap(this.dataStore, outer, min);
        }
    }
    function bubbleSort() {
        var numElements = this.dataStore.length;
        for (var outer = numElements; outer >= 2; --outer) {
            for (var inner = 0; inner < outer - 1; ++inner) {
                if (this.dataStore[inner] > this.dataStore[inner + 1]) {
                    this.swap(this.dataStore, inner, inner + 1);
                }
            }
        }
    }
    function insertionSort() {
      var temp, inner;
      for (var outer = 1; outer <= this.dataStore.length - 1; ++outer) {
        temp = this.dataStore[outer];
        inner = outer;
        while (inner > 0 && (this.dataStore[inner - 1] >= temp)) {
          this.dataStore[inner] = this.dataStore[inner - 1];
          --inner;
        }
        this.dataStore[inner] = temp;
      }
    }
    function shellsort() {
      var temp;
      for (var g = 0; g < this.gaps.length; ++g) {
        for (var i = this.gaps[g]; i < this.dataStore.length; ++i) {
          temp = this.dataStore[i];
          for (var j = i; j >= this.gaps[g] && this.dataStore[j-this.gaps[g]] > temp; j -= this.gaps[g]) {
            this.dataStore[j] = this.dataStore[j - this.gaps[g]];
          }
          this.dataStore[j] = temp;
        }
      }
    }
    function shellsort1() {
      var N = this.dataStore.length;
      var h = 1;
      while (h < N/3) {
          h = 3 * h + 1;
      }
      while (h >= 1) {
          for (var i = h; i < N; i ++) {
              for (var j = i; j >= h && this.dataStore[j] < this.dataStore[j-h]; j -= h) {
                  this.swap(this.dataStore, j, j - h);
              }
          }
          h = (h-1)/3;
      }
    }
    function mergeSort() {
      var arr = this.dataStore;
      if (arr.length < 2) {
        return;
      }
      var step = 1;
      var left, right;
      while (step < arr.length) {
        left = 0;
        right = step;
        while (right + step <= arr.length) {
          this.mergeArrays(arr, left, left+step, right, right+step);
          left = right + step;
          right = left + step;
        }
        if (right < arr.length) {
          this.mergeArrays(arr, left, left+step, right, arr.length);
        }
        step *= 2;
      }
    }
    function mergeArrays(arr, startLeft, stopLeft, startRight, stopRight) {
      var rightArr = new Array(stopRight - startRight + 1);
      var leftArr = new Array(stopLeft - startLeft + 1);
      k = startRight;
      for (var i = 0; i < (rightArr.length-1); ++i) {
        rightArr[i] = arr[k];
        ++k;
      }
      k = startLeft;
      for (var i = 0; i < (leftArr.length-1); ++i) {
        leftArr[i] = arr[k];
        ++k;
      }
      rightArr[rightArr.length - 1] = Infinity;
      leftArr[leftArr.length - 1] = Infinity;
      var m = 0;
      var n = 0;
      for (var k = startLeft; k < stopRight; ++k) {
        if (leftArr[m] <= rightArr[n]) {
          arr[k] = leftArr[m];
          m++;
        } else {
          arr[k] = rightArr[n];
          n++;
        }
      }
    }
    function qSort(list) {
        var list;
        if (list.length == 0) {
            return [];
        }
        var lesser = [];
        var greater = [];
        var pivot = list[0];
        for (var i = 1; i < list.length; i ++) {
          if (list[i] < pivot) {
            lesser.push(list[i]);
          } else {
            greater.push(list[i]);
          }
        }
        return this.qSort(lesser).concat(pivot, this.qSort(greater));
    }
    var numElements = 200000;
    var myNums = new CArray(numElements);
    myNums.setData();
    // console.log(myNums.toString());
    var startTime = new Date().getTime();
    // Mynums. Insertionsort(); / / about 27ms
    // Mynums. Bubblesort(); / / about 100ms
    // Mynums. Selectionsort(); / / about 50ms
    // Mynums. Shellsort(); / / about 20ms
    // Mynums. Shellsort1(); / / about 8ms
    // Mynums. Mergesort(); / / about 9ms
    myNums.dataStore = myNums.qSort(myNums.dataStore); // About 17ms
    var endTime = new Date().getTime();
    console.log('time consuming: ' + (endTime - startTime) + 'Millisecond');
    // console.log(myNums.toString());
    
  </script>
</body>
</html>

Reference resources

1. JavaScript description of data structure and algorithm