brief introduction

Prefix tree is also called word lookup tree, Trie tree , is a kind of tree structure , is a variant of hash tree. The typical application is to count, sort and save a large number of data character String (but not limited to string), so it is often used by search engine system for text word frequency statistics. Its advantages are: using the common prefix of string to reduce the query time, minimize unnecessary string comparison, and the query efficiency is higher than that of hash tree.
It has three basic properties: the root node does not contain characters, and each node contains only one character except the root node; From the root node to a node, the characters passing through the path are connected to the corresponding string of the node; All child nodes of each node contain different characters.

example

subject

Trie (pronounced like "try") or prefix tree is a tree data structure used to efficiently store and retrieve keys in string data sets. This data structure has many application scenarios, such as automatic completion and spell checking.

Please implement the Trie class:

Trie() initializes the prefix tree object.
void insert(String word) inserts the string word into the prefix tree.
boolean search(String word) returns true if the string word is in the prefix tree (that is, it has been inserted before retrieval); Otherwise, false is returned.
boolean startsWith(String prefix) returns true if one of the prefixes of the previously inserted string word is prefix; Otherwise, false is returned.

Source: LeetCode
Link: https://leetcode-cn.com/problems/implement-trie-prefix-tree
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

Examples

input

["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]

output

[null, null, true, false, true, null, true]

explain

Trie trie = new Trie();

trie.insert("apple");

trie.search(“apple”); // Return True

trie.search(“app”); // Return False

trie.startsWith(“app”); // Return True

trie.insert("app");

trie.search(“app”); // Return True

code implementation

thinking

Prefix tree is essentially a tree structure. Each node stores one letter and connects the next letter. In this way, multiple letters are connected to form a complete word, as shown in the figure below:

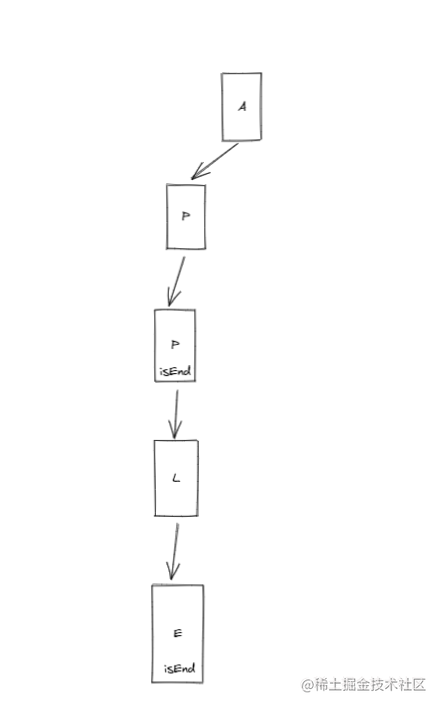
The above figure can represent two words: APP and APPLE. When looking for words, we should rush to the root node until the isEnd tag is matched, then all letters from the root node to the node can form a complete word. The specific implementation code is as follows:

code

/**
 * Initialize your data structure here.
 */
var Trie = function() {
    this.tree = {};
};

/**
 * Inserts a word into the trie. 
 * @param {string} word
 * @return {void}
 */
Trie.prototype.insert = function(word) {
    let tree = this.tree;
    for(const w of word){
        if(tree[w] == undefined){
            tree[w] = {};
        }
        tree = tree[w];
    }
    tree.isEnd = true;
};

/**
 * Returns if the word is in the trie. 
 * @param {string} word
 * @return {boolean}
 */
Trie.prototype.search = function(word) {
    let tree = this.tree;
    for(const w of word){
        if(tree[w] == undefined){
            return false;
        }
        tree = tree[w];
    }
    return tree.isEnd == true;
};

/**
 * Returns if there is any word in the trie that starts with the given prefix. 
 * @param {string} prefix
 * @return {boolean}
 */
Trie.prototype.startsWith = function(prefix) {
    let tree = this.tree;
    for(const w of prefix){
        if(tree[w] == undefined){
            return false;
        }
        tree = tree[w];
    }
    return true;
};

/**
 * Your Trie object will be instantiated and called as such:
 * var obj = new Trie()
 * obj.insert(word)
 * var param_2 = obj.search(word)
 * var param_3 = obj.startsWith(prefix)
 */

application

Prefix trees can be used in many places, such as:

Fast retrieval of string

Give a familiar vocabulary composed of N words and an article written in lowercase English. Please write all new words that are not in the familiar vocabulary in the order of the earliest occurrence.
In this problem, we can use array enumeration, hash and dictionary tree to build a tree of familiar words, and then read them into the article for comparison. This method is more efficient.

"String" sorting

Given N different English names composed of only one word, let you output them from small to large according to the dictionary order, sort them with the dictionary tree, and create the dictionary tree in the form of array. All the sons of each node of the tree are obviously sorted according to their letter size. The tree can be traversed in sequence.

Longest Common Prefix

Establish a dictionary tree for all strings. The length of the longest common prefix of two strings is the number of common ancestors of their nodes. Therefore, the problem is transformed into the problem of common ancestors at that time.