Binary tree and binary lookup tree
Tree is a nonlinear data structure, which stores data in a hierarchical manner. Trees are used to store hierarchical data, such as files in the file system; Trees are also used to store sequence tables.
Binary tree is a special tree with no more than two child nodes. Binary tree has some special computational properties, which makes some operations on them extremely efficient. Along a specific set of edges, it can go from one node to another node that is not directly connected to it. This group of edges from one node to another is called a path. The tree can be divided into several levels. The root node is level 0, its child node is level 1, the child node of the child node is level 2, and so on. The nodes of any layer in the tree can be regarded as the root of the subtree, which includes the child nodes of the root node, the child nodes of the child nodes, etc. We define the number of layers of the tree as the depth of the tree. Each node has a value related to it, which is sometimes called a key. The distance from one node to another is called a path
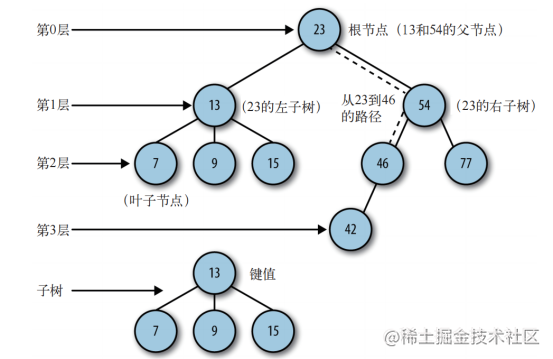
Each node of a binary tree cannot have more than two child nodes. By limiting the number of child nodes to 2, we can write an efficient program to insert, find and delete data in the tree. The two child nodes of a parent node are called left node and right node respectively. In some binary tree implementations, the left node contains a specific set of values and the right node contains another specific set of values.
When considering a special binary tree, such as binary lookup tree, it is very important to determine the child nodes.
Binary lookup tree is a special binary tree. Relatively small values are saved in the left node and larger values are saved in the right node. This feature makes the search efficient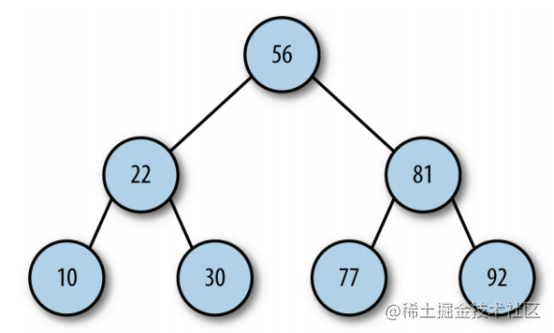
The following implements a binary lookup tree
Definition of Node class
Each node contains three elements
- Key value data
- left node pointer
right node pointer
class Node{ constructor(data, left, right){ this.data = data; this.left = left; this.right = right; } show(){ return this.data } }
Binary lookup tree class
Initialize root node root is null
class BST{
root=null
constructor(){
}
}The insert() method is used to add new nodes to the tree
insert(data) {
let node = new Node(data, null, null)
if (this.root == null) {
this.root = node
} else {
let current = this.root
let parent
while (true) {
parent = current
if (data < current.data) {
current = current.left
if (current == null) {
parent.left = node
break;
}
} else {
current = current.right
if (current == null) {
parent.right = node
break;
}
}
}
}
}Traversing binary search tree
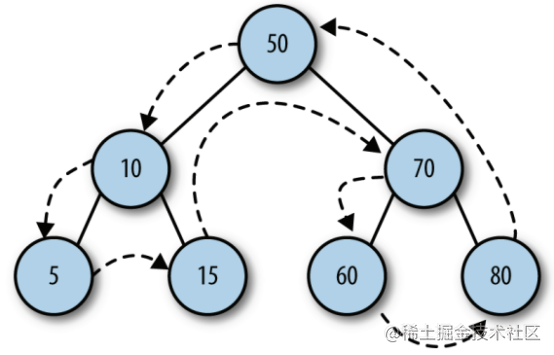
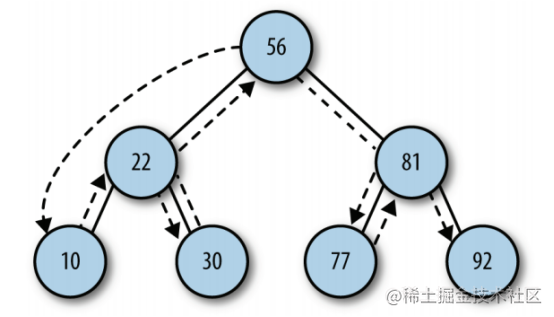
There are three ways to traverse BST: middle order, first order and second order. Middle order traversal accesses all nodes on the BST in ascending order according to the key values on the nodes. The first order traversal first accesses the root node, and then accesses the left and right subtrees in the same way. The subsequent traversal first accesses the leaf node, from the left subtree to the right subtree, and then to the root node.
preOrder()
preOrder(node) {
if (node != null) {
console.log(node.show())
this.inOrder(node.left)
this.inOrder(node.right)
}
}Middle order traversal inOrder()
inOrder(node) {
if (node != null) {
this.inOrder(node.left)
console.log(node.show())
this.inOrder(node.right)
}
}Post order traversal ()
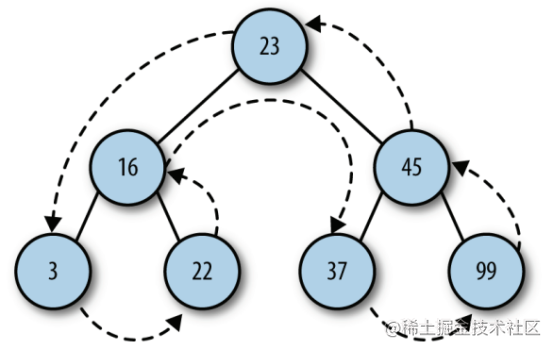
postOrder(node) {
if (node != null) {
this.inOrder(node.left)
this.inOrder(node.right)
console.log(node.show())
}
}getMin() finds the minimum value
The minimum value is on the far left. Uniformly traverse the left elements and find the last element, which is the minimum value
getMin() {
let node = this.root
while (node.left != null) {
node = node.left
}
return node.data
}getMax() finds the maximum value
The maximum value is on the far right. Uniformly traverse the right elements and find the last element, which is the maximum value
getMax() {
let node = this.root
while (node.right != null) {
node = node.right
}
return node.data
}find() finds the node with the specified value
find(data) {
let node = this.root
let result = null
while (node) {
if (node.data == data) {
result = node
break
}
if (node.data < data) {
node = node.right
} else {
node = node.left
}
}
Delete node from binary lookup tree
Deleting a node on the BST is the most complex operation, and its complexity depends on which node is deleted. If you delete a node without child nodes, it is very simple. You can directly remove the node. If the node has only one child node, whether it is a left child node or a right child node, it becomes a little complicated. You need to point the pointer of the parent node to the deleted node to the corresponding left child node and the live right child node. Deleting a node containing two child nodes is the most complex. You need to replace the smallest node in the right subtree or the smallest node in the left subtree.
To manage the complexity of the delete operation, we use recursive operations and define two methods at the same time: remove() and removeNode().
remove(data) {
this.root = this.removeNode(this.root, data)
}
removeNode(node, data) {
if (node == null) {
return null
}
if (node.data == data) {
if (node.left == null && node.right == null) {
return null
}
if (node.left == null) {
return node.right
}
if (node.right !== null) {
return node.left
}
let smallestNode = this.getSmallest(node.right)
node.data = smallestNode.data
this.removeNode(node.right, smallestNode.data)
return node
} else if (node.data < data) {
node.right = this.removeNode(node.right.data)
} else {
node.left = this.removeNode(node.left.data)
}
}
getSmallest(node) {
while (node.left != null) {
node = node.left
}
return node
}Complete code
class Node {
constructor(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
}
show() {
return this.data
}
}
class BST {
root = null
constructor() {
}
insert(data) {
let node = new Node(data, null, null)
if (this.root == null) {
this.root = node
} else {
let current = this.root
let parent
while (true) {
parent = current
if (data < current.data) {
current = current.left
if (current == null) {
parent.left = node
break;
}
} else {
current = current.right
if (current == null) {
parent.right = node
break;
}
}
}
}
}
inOrder(node) {
if (node != null) {
this.inOrder(node.left)
console.log(node.show())
this.inOrder(node.right)
}
}
preOrder(node) {
if (node != null) {
console.log(node.show())
this.inOrder(node.left)
this.inOrder(node.right)
}
}
postOrder(node) {
if (node != null) {
this.inOrder(node.left)
this.inOrder(node.right)
console.log(node.show())
}
}
getMin() {
let node = this.root
while (node.left != null) {
node = node.left
}
return node.data
}
getMax() {
let node = this.root
while (node.right != null) {
node = node.right
}
return node.data
}
find(data) {
let node = this.root
let result = null
while (node) {
if (node.data == data) {
result = node
break
}
if (node.data < data) {
node = node.right
} else {
node = node.left
}
}
return result
}
remove(data) {
this.root = this.removeNode(this.root, data)
}
removeNode(node, data) {
if (node == null) {
return null
}
if (node.data == data) {
if (node.left == null && node.right == null) {
return null
}
if (node.left == null) {
return node.right
}
if (node.right !== null) {
return node.left
}
let smallestNode = this.getSmallest(node.right)
node.data = smallestNode.data
this.removeNode(node.right, smallestNode.data)
return node
} else if (node.data < data) {
node.right = this.removeNode(node.right.data)
} else {
node.left = this.removeNode(node.left.data)
}
}
getSmallest(node) {
while (node.left != null) {
node = node.left
}
return node
}
}chart
A graph consists of a set of edges and a set of vertices. Edges are defined by vertex pairs (v1,v2). v1 and v2 are the two vertices in the graph respectively. Vertices also have weights. If the vertex pairs of a graph are ordered, it can be called a directed graph. After sorting the vertex pairs in a directed graph, you can draw an arrow between the two vertices. A directed graph shows the flow direction of vertices.
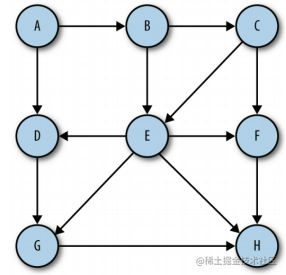
If a graph is unordered, it is called an unordered graph
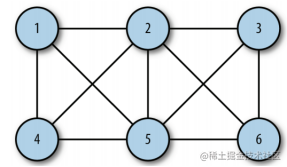
We call the method of representing the edges of a graph adjacency table or adjacency table array. In this method, edges are stored as an array of adjacent vertex lists of vertices, and the vertices are used as indexes.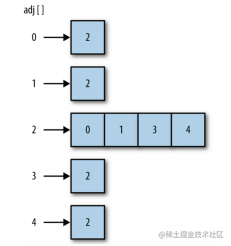
The following implementation diagram class
Represents a vertex
class Vertex{
constructor(label){
this.label=label
}
}Construction diagram
class Graph{
edges=0
adj=[]
vertices=0
marked=[]
edgeTo=[]
constructor(v){
this.vertices = v
for(let index=0;index < this.vertices;index++){
this.adj[index]=[]
this.marked[index]=false
}
}
}addEdge() add node
addEdge(v,w){
this.adj[v].push(w)
this.adj[w].push(v)
this.edges++
}The showGraph() function displays the graph by printing a list of all vertices and their adjacent vertices
showGraph() {
for (var i = 0; i < this.vertices; ++i) {
let resStr = `${i}-> `
for (var j = 0; j < this.vertices; ++j ) {
if (this.adj[i][j] != undefined) {
resStr=resStr+`${this.adj[i][j]} `
}
}
console.log(resStr)
}
}Depth first search
Depth first search includes tracing from the starting vertex of a path until it reaches the last vertex, then tracing back, continuing to trace the next path until it reaches the last vertex, and so on until there is no path. This is not a search for a specific path, but a search to see which paths can be selected in the diagram
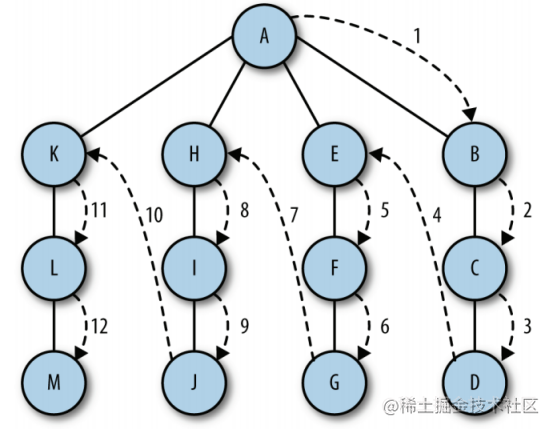
dfs(v){
this.marked[v]=true
if(this.adj[v] != undefined){
console.log("Visited vertex: " + v)
}
for(let key of this.adj[v]){
if(!this.marked[key]){
this.dfs(key)
}
}
}Breadth first search
Breadth first search starts with the first vertex and tries to access the vertex as close to it as possible. In essence, this search moves layer by layer on the graph. First, check the layer closest to the first vertex, and then gradually move down to the layer furthest from the starting vertex
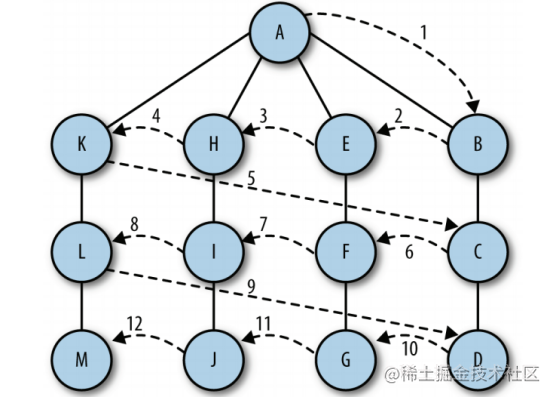
bfs(s){
let queue = []
this.marked[s] = true
queue.push(s)
while(queue.length>0){
let v = queue.shift()
if(v == undefined){
console.log(`Visisted vertex: ${v}`)
}
for(let key of this.adj[v]){
if(!this.marked[key]){
this.edgeTo[key]=v
this.marked[key] = true
queue.push(key)
}
}
}
}Complete code
class Vertex{
constructor(label){
this.label=label
}
}
class Graph{
edges=0
adj=[]
vertices=0
marked=[]
edgeTo=[]
constructor(v){
this.vertices = v
for(let index=0;index < this.vertices;index++){
this.adj[index]=[]
this.marked[index]=false
}
}
addEdge(v,w){
this.adj[v].push(w)
this.adj[w].push(v)
this.edges++
}
showGraph() {
for (var i = 0; i < this.vertices; ++i) {
let resStr = `${i}-> `
for (var j = 0; j < this.vertices; ++j ) {
if (this.adj[i][j] != undefined) {
resStr=resStr+`${this.adj[i][j]} `
}
}
console.log(resStr)
}
}
dfs(v){
this.marked[v]=true
if(this.adj[v] != undefined){
console.log("Visited vertex: " + v)
}
for(let key of this.adj[v]){
if(!this.marked[key]){
this.dfs(key)
}
}
}
bfs(s){
let queue = []
this.marked[s] = true
queue.push(s)
while(queue.length>0){
let v = queue.shift()
if(v == undefined){
console.log(`Visisted vertex: ${v}`)
}
for(let key of this.adj[v]){
if(!this.marked[key]){
this.edgeTo[key]=v
this.marked[key] = true
queue.push(key)
}
}
}
}
}